Python 中的增强 dickey-fuller 测试(带有示例)
如果时间序列没有趋势、随着时间的推移呈现恒定的方差并且随着时间的推移具有恒定的自相关结构,则该时间序列被称为“平稳”。
测试时间序列是否平稳的一种方法是执行增强迪基-富勒检验,该检验使用以下原假设和备择假设:
H 0 :时间序列是非平稳的。换句话说,它的结构取决于时间,并且它的变化并不随时间恒定。
H A :时间序列是平稳的。
如果检验的p 值低于一定的显着性水平(例如 α = 0.05),那么我们可以拒绝原假设并得出时间序列平稳的结论。
以下分步示例演示如何在 Python 中针对给定时间序列执行增强的 Dickey-Fuller 测试。
示例:Python 中的增强 Dickey-Fuller 测试
假设我们在Python中有以下时间序列数据:
data = [3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10]
在对数据执行增强的 Dickey-Fuller 测试之前,我们可以创建一个快速绘图来可视化数据:
import matplotlib. pyplot as plt plt. plot (data)
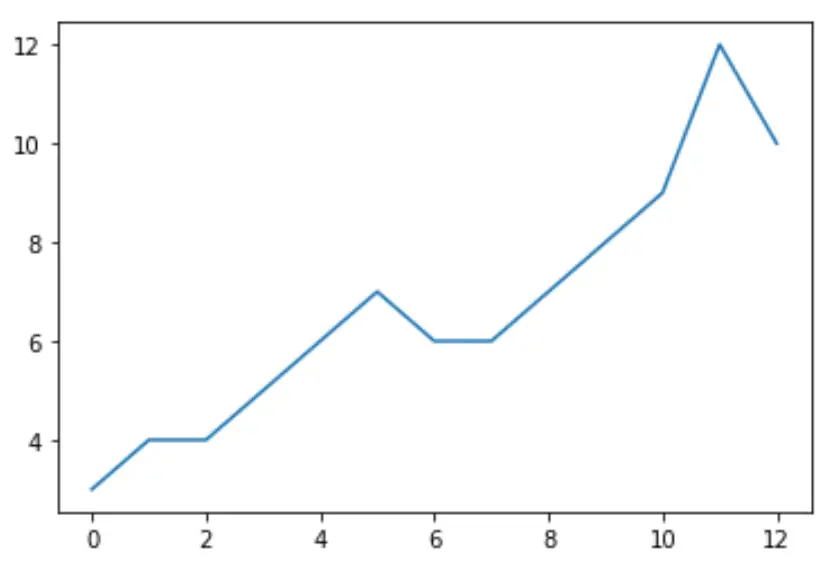
要执行增强的 Dickey-Fuller 测试,我们可以使用statsmodels库中的adfuller()函数。首先,我们需要安装 statsmodels:
pip install statsmodels
然后我们可以使用以下代码来执行增强的Dickey-Fuller测试:
from statsmodels. tsa . stattools import adfuller #perform augmented Dickey-Fuller test adfuller(data) (-0.9753836234744063, 0.7621363564361013, 0, 12, {'1%': -4.137829282407408, '5%': -3.1549724074074077, '10%': -2.7144769444444443}, 31.2466098872313)
以下是如何解释结果中最重要的值:
- 检验统计量: -0.97538
- P 值: 0.7621
由于 p 值不小于 0.05,因此我们无法拒绝原假设。
这意味着时间序列不是平稳的。换句话说,它的结构取决于时间,并且它的变化并不随时间恒定。
其他资源
如何在 Matplotlib 中绘制时间序列
如何从 Pandas DataFrame 绘制多个系列
如何使用 Python 执行 Mann-Kendall 趋势检验