协方差矩阵
本文解释什么是协方差矩阵以及它的公式是什么。您将通过具体示例了解如何创建协方差矩阵以及协方差矩阵的属性。
什么是协方差矩阵?
协方差矩阵是一个方阵,其元素是所研究变量的方差和协方差。因此,协方差矩阵主对角线的元素是每个变量的方差,其余元素是变量之间的协方差。
在统计学中,协方差矩阵用于分析两个或多个随机变量之间的关系。协方差矩阵非常有用,因为它可以让您快速解释许多变量之间的相关性,因为您可以同时看到变量的所有协方差的值。
协方差矩阵的符号是大写希腊字母西格玛(Σ)。
如何计算协方差矩阵
要计算多个统计变量的协方差矩阵,必须执行以下步骤:
- 计算所有变量的方差。
- 计算每对变量的协方差。
- 形成协方差矩阵:
- 变量i的方差必须放置在矩阵的主对角线上,更准确地说是放置在位置i,i上。
- 变量i和j之间的协方差必须放在矩阵的i,j位置。
因此协方差矩阵的公式如下:
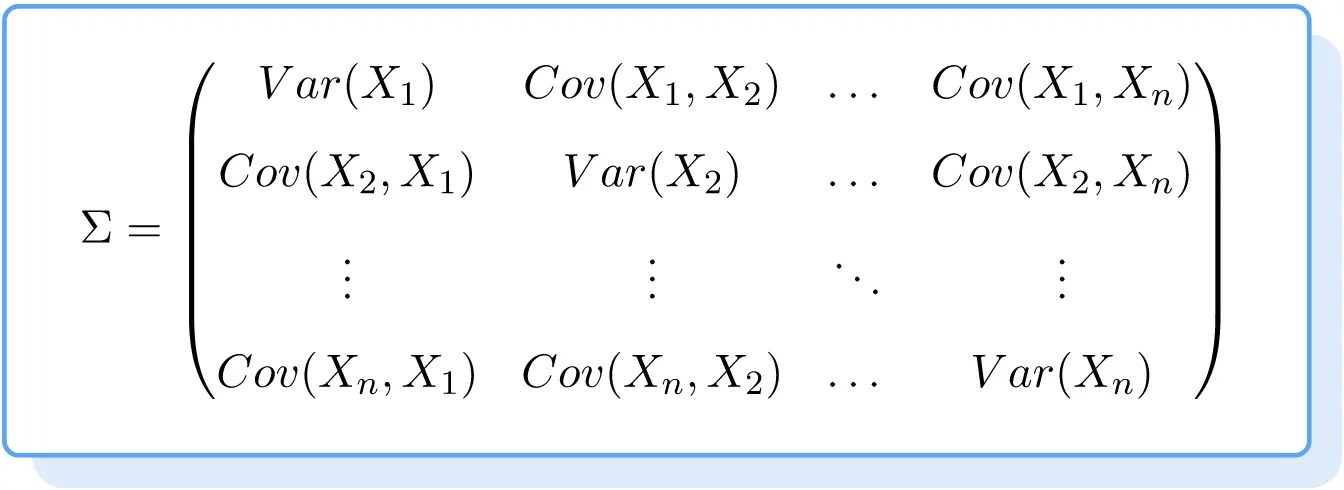
协方差矩阵示例
看到协方差矩阵的定义后,下面是一个分步练习,以便您可以了解这种类型的矩阵是如何制作的。
计算变量X、Y和Z的协方差矩阵,其值为:
- X:4、7、12、5、7
- 还有:9、15、19、6、8
- Z:7、2、4、6、3
我们需要做的第一件事是确定所有变量的方差:
![]()
![]()
![]()
➤请参阅:间隙计算器
其次,我们找到每对变量之间的协方差:
![]()
![]()
![]()
➤请参阅:协方差计算器
一旦我们计算了所有方差和协方差,剩下的就是制作协方差矩阵。为此,我们将方差值放在矩阵的主对角线上,将协方差值放在其相应的位置:
![Rendered by QuickLaTeX.com \Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3a423b40ad6d25b57327b1f3dccd5df4_l3.png)
![Rendered by QuickLaTeX.com \Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d90c58cc3c8ecef6a85c88196e1dd08d_l3.png)
正如您所看到的,通过在矩阵中表示方差和协方差,可以很容易地解释变量。离差最大的变量是 Y (23.44),另一方面,变量 X 和 Y 具有正相关关系,而变量 X 和 Z(因此 Y 和 Z)具有反相关关系。
请注意,协方差矩阵始终是对称的,因为两个变量之间的协方差不取决于变量的顺序。例如,
![]()
等于
![]()
此外,协方差矩阵始终是方阵,其维度将等于变量的数量。在本例中,我们有三个变量,这就是为什么它是 3×3 矩阵,但如果我们只有两个变量,协方差矩阵将为 2×2。
协方差矩阵的属性
协方差矩阵具有以下特点:
- 协方差矩阵是变量数量阶的方阵。
- 协方差矩阵是对称的,这意味着矩阵的主对角线是对称轴。
- 协方差矩阵始终是半正定的。
- 协方差矩阵的行列式等于或大于零。