逆正态分布：定义和示例

术语逆正态分布是指使用已知概率在正态分布中找到相应的 z 临界值的方法。

这不应与逆高斯分布混淆，逆高斯分布是连续概率分布。

本教程提供了在不同统计软件中使用逆正态分布的几个示例。

逆正态分布我们有 TI-83 或 TI-84 计算器

您最有可能在 TI-83 或 TI-84 计算器上遇到术语“逆正态分布”，它使用以下函数来查找与特定概率对应的临界 z 值：

invNorm(概率, μ, σ)

金子：

• 概率：显着性水平
• μ：总体平均值
• σ：总体标准差

您可以通过按2nd然后按vars在 TI-84 计算器上访问此功能。这将带您进入DISTR屏幕，然后您可以在其中使用invNorm() ：

例如，我们可以使用此函数来查找与概率值 0.05 相对应的 z 临界值：

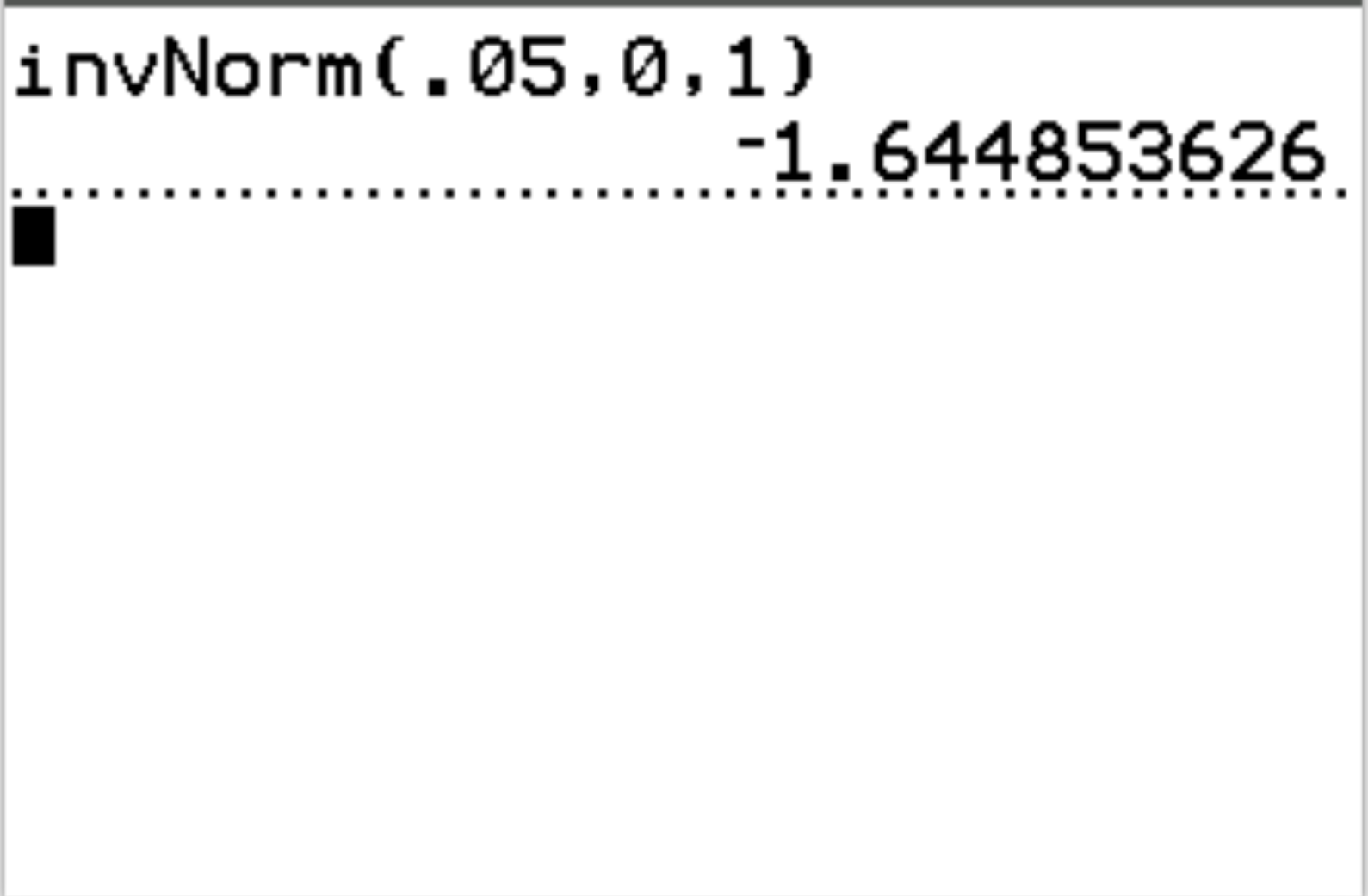
与概率值 0.05 对应的临界 z 值为-1.64485 。

相关：如何在 TI-84 计算器上使用 invNorm（带有示例）

Excel 中的逆正态分布

要在 Excel 中查找与某个概率值相关的 z 临界值，我们可以使用INVNORM()函数，该函数使用以下语法：

INVNORM(p, 平均值, 标准差)

金子：

• p：显着性水平
• 平均数：人口平均数
• SD：总体标准差

例如，我们可以使用此函数来查找与概率值 0.05 相对应的 z 临界值：

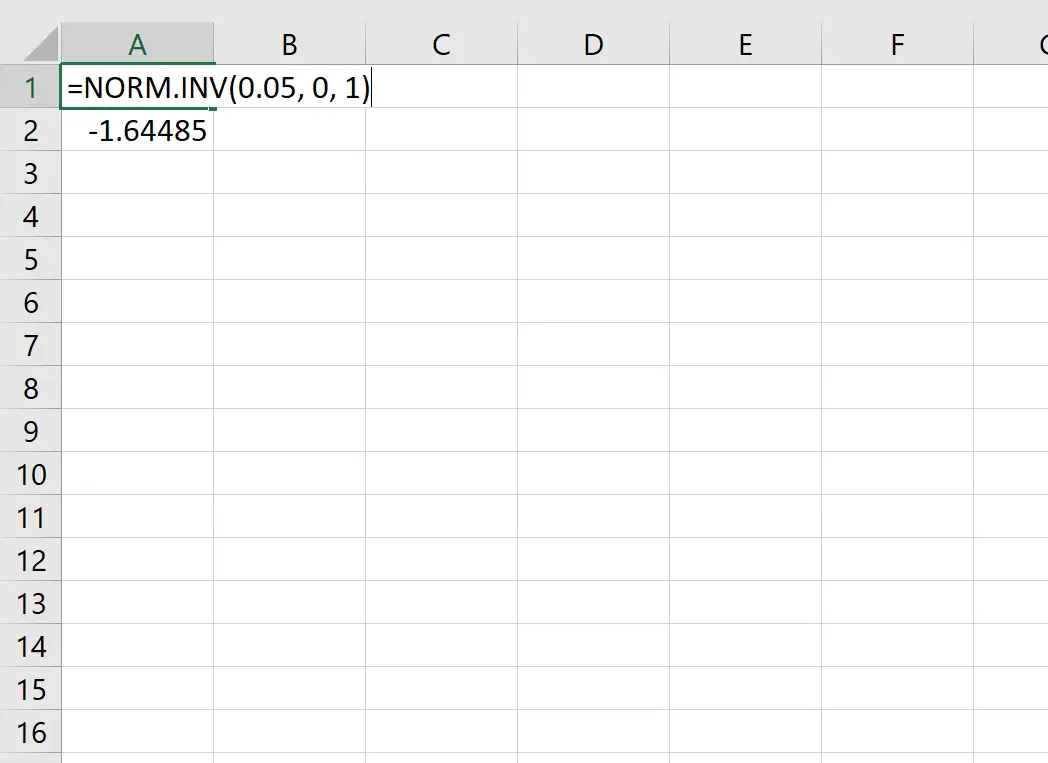
与概率值 0.05 对应的临界 z 值为-1.64485 。

R 中的逆正态分布

为了找到与 R 中某个概率值相关的 z 临界值，我们可以使用qnorm()函数，该函数使用以下语法：

qnorm（p、平均值、标准差）

金子：

• p：显着性水平
• 平均数：人口平均数
• SD：总体标准差

例如，我们可以使用此函数来查找与概率值 0.05 相对应的 z 临界值：

 qnorm (p= .05 , mean= 0 , sd= 1 )

[1] -1.644854

同样，对应于概率值 0.05 的临界 z 值为-1.64485 。