如何在 sas 中执行逐步回归（附示例）

逐步回归是一个过程，我们可以用它来从一组预测变量构建回归模型，方法是在模型中逐步输入和删除预测变量，直到不再有统计学上有效的理由来输入或删除预测变量。删除更多。

逐步回归的目标是创建一个回归模型，其中包括与响应变量在统计上显着相关的所有预测变量。

要在 SAS 中执行逐步回归，您可以将PROC REG与SELECTION语句结合使用。

以下示例展示了如何在实践中在 SAS 中执行逐步回归。

示例：在 SAS 中执行逐步回归

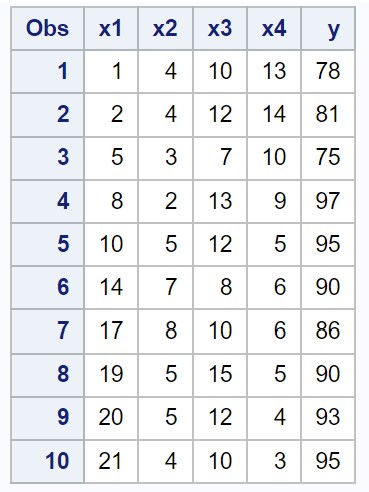
假设我们在 SAS 中有以下数据集，其中包含四个预测变量 (x1、x2、x3、x4) 和一个响应变量 (y)：

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

现在假设我们想要确定哪种预测变量组合将产生最佳的多元线性回归模型。

当我们谈论“最佳”回归模型时，我们指的是最大化或最小化某些度量的模型。

我们通常使用两个指标来评估一组潜在模型中哪种回归模型最好：

1. 调整后的 R 平方：调整后的 R 平方值告诉我们模型的有用性，该值根据模型中预测变量的数量进行调整。具有最高调整 R 平方值的模型被认为是最好的。

2. AIC ：赤池信息准则（AIC）是用于比较不同回归模型拟合程度的指标。 AIC 值最低的模型被认为是最好的。

幸运的是，我们可以使用PROC REG和SELECTION语句来计算 SAS 中回归模型的拟合 R 平方和 AIC 值。

以下代码展示了如何执行此操作：

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

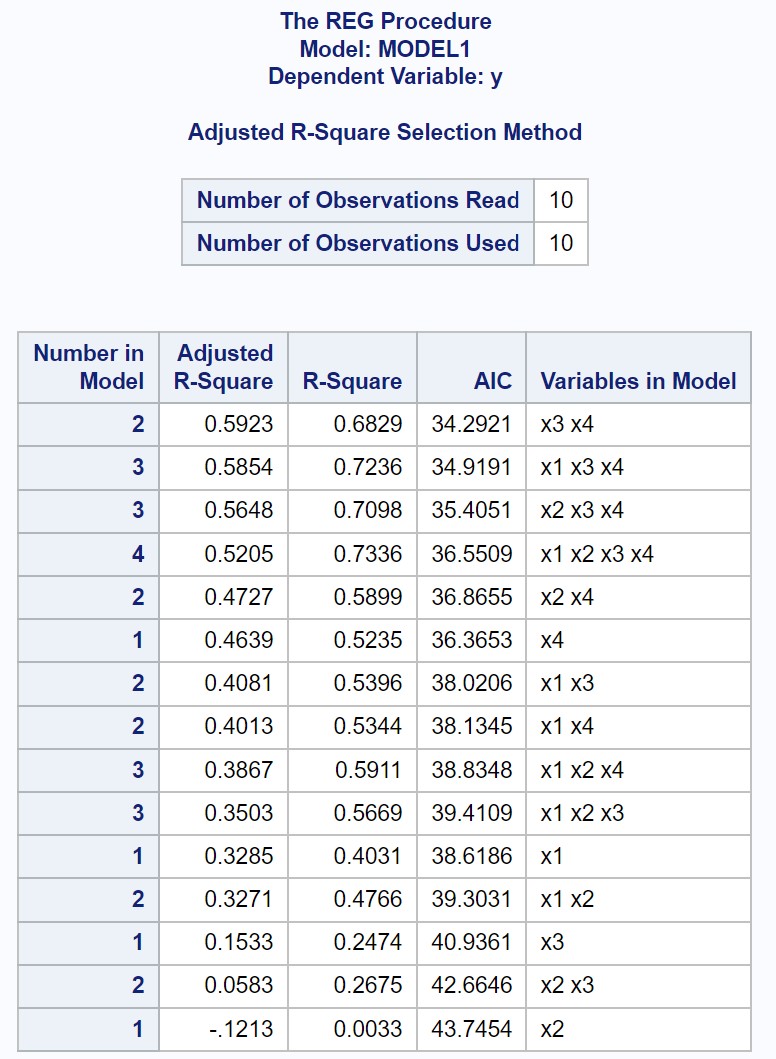
输出显示每个可能的多元线性回归模型的拟合 R 平方和 AIC 值。

从结果中我们可以看出，调整后的 R 平方值最高且AIC 值最低的值为仅使用 x3 和 x4 作为预测变量的回归模型。

因此，我们声明以下模型是所有可能模型中“最好的”：

y = b ₀ + b ₁ (x3) + b ₂ (x4)

这个特定的回归模型具有以下指标：

• 调整后的 R 平方值： 0.5923
• AIC： 34.2921

选择“最佳”回归模型的注意事项

请注意，有时具有最高调整 R 平方值的模型并不总是具有最低的 AIC 值。

在决定哪种回归模型最好时，调整后的 R 平方和 AIC 可作为建议，但在现实世界中，您可能需要使用领域专业知识来确定哪种模型最好。

选择简约模型也可能是明智的，即使用尽可能少的预测变量实现所需拟合水平的模型。

此类模型背后的推理源于 奥卡姆剃刀的思想（有时称为“简约原则”），该思想认为最简单的解释可能是正确的。

应用于统计学时，参数较少但拟合程度令人满意的模型应该优于参数较多且拟合程度稍高的模型。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在 SAS 中执行简单线性回归
如何在 SAS 中执行多元线性回归
如何在 SAS 中执行多项式回归
如何在 SAS 中执行逻辑回归