如何在 python 中执行逻辑回归（逐步）

当响应变量是二元时，逻辑回归是我们可以用来拟合回归模型的方法。

逻辑回归使用称为最大似然估计的方法来查找以下形式的方程：

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

金子：

• X _j ：第 j^个预测变量
• β _j ：第 j^个预测变量的系数估计

方程右侧的公式预测响应变量取值 1 的对数几率。

因此，当我们拟合逻辑回归模型时，我们可以使用以下方程来计算给定观测值为 1 的概率：

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

然后我们使用一定的概率阈值将观察结果分类为 1 或 0。

例如，我们可以说概率大于或等于 0.5 的观测值将被分类为“1”，所有其他观测值将被分类为“0”。

本教程提供了如何在 R 中执行逻辑回归的分步示例。

第1步：导入必要的包

首先，我们将导入必要的包以在 Python 中执行逻辑回归：

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

第2步：加载数据

对于此示例，我们将使用《统计学习简介》一书中的默认数据集。我们可以使用以下代码来加载并显示数据集的摘要：

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

该数据集包含 10,000 人的以下信息：

• 违约：表明个人是否违约。
• 学生：表明个人是否是学生。
• 余额：个人持有的平均余额。
• 收入：个人的收入。

我们将使用学生身份、银行余额和收入构建逻辑回归模型，预测给定个人违约的概率。

第 3 步：创建训练和测试样本

接下来，我们将数据集分为用于训练模型的训练集和用于测试模型的测试集。

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

步骤 4：拟合逻辑回归模型

接下来，我们将使用LogisticRegression()函数将逻辑回归模型拟合到数据集：

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

第 5 步：模型诊断

一旦我们拟合了回归模型，我们就可以分析模型在测试数据集上的性能。

首先，我们将为模型创建混淆矩阵：

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

从混淆矩阵我们可以看出：

• #真实阳性预测：2886
• #真实的负面预测：0
• #误报预测：113
• #假阴性预测：1

我们还可以获得准确率模型，它告诉我们模型做出的校正预测的百分比：

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

这告诉我们，该模型在96.2%的情况下对个人是否会违约做出了正确的预测。

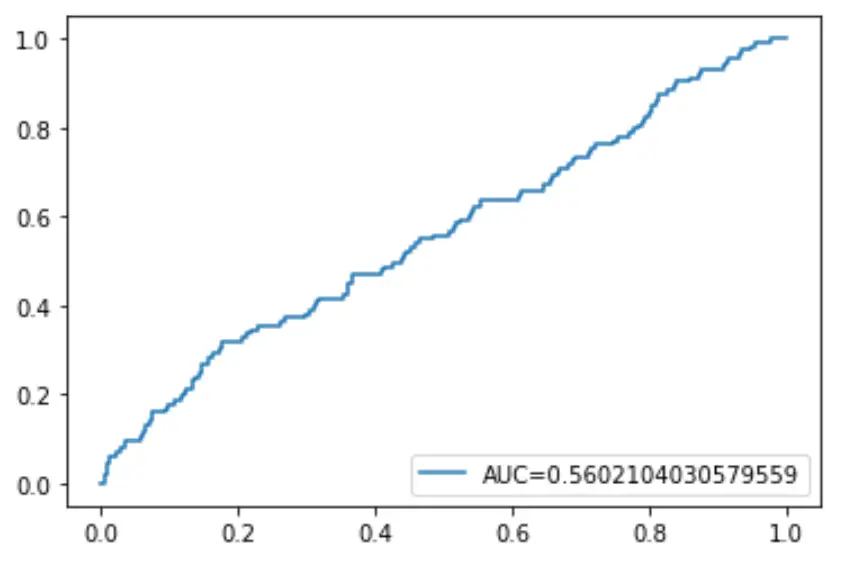
最后，我们可以绘制接收者操作特征（ROC）曲线，该曲线显示当预测概率阈值从 1 降低到 0 时模型预测的真阳性百分比。

AUC（曲线下面积）越高，我们的模型预测结果就越准确：

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()