如何在stata中进行逻辑回归

逻辑回归是当响应变量是二元时我们用来拟合回归模型的方法。以下是使用逻辑回归的一些示例：

• 我们想知道运动、饮食和体重如何影响心脏病发作的可能性。响应变量是心脏病发作，它有两种潜在结果：心脏病发作发生或不发生。
• 我们想知道 GPA、ACT 分数和修读的 AP 课程数量如何影响被特定大学录取的可能性。响应变量是接受，它有两种潜在结果：接受或不接受。
• 我们想知道字数和电子邮件标题是否会影响电子邮件为垃圾邮件的可能性。响应变量是垃圾邮件，它有两种潜在结果：垃圾邮件或非垃圾邮件。

本教程介绍如何在 Stata 中执行逻辑回归。

示例：Stata 中的逻辑回归

假设我们想了解母亲的年龄和吸烟习惯是否会影响低出生体重婴儿的可能性。

为了探索这一点，我们可以使用年龄和吸烟（是或否）作为解释变量，并使用低出生体重（是或否）作为响应变量来进行逻辑回归。由于响应变量是二元的——只有两种可能的结果——应该使用逻辑回归。

在 Stata 中完成以下步骤，使用名为lbw的数据集执行逻辑回归，该数据集包含 189 位不同母亲的数据。

第 1 步：加载数据。

通过在命令框中键入以下内容来加载数据：

使用https://www.stata-press.com/data/r13/lbw

步骤 2：获取数据摘要。

通过在命令框中键入以下内容，可以快速了解您正在使用的数据：

总结一下

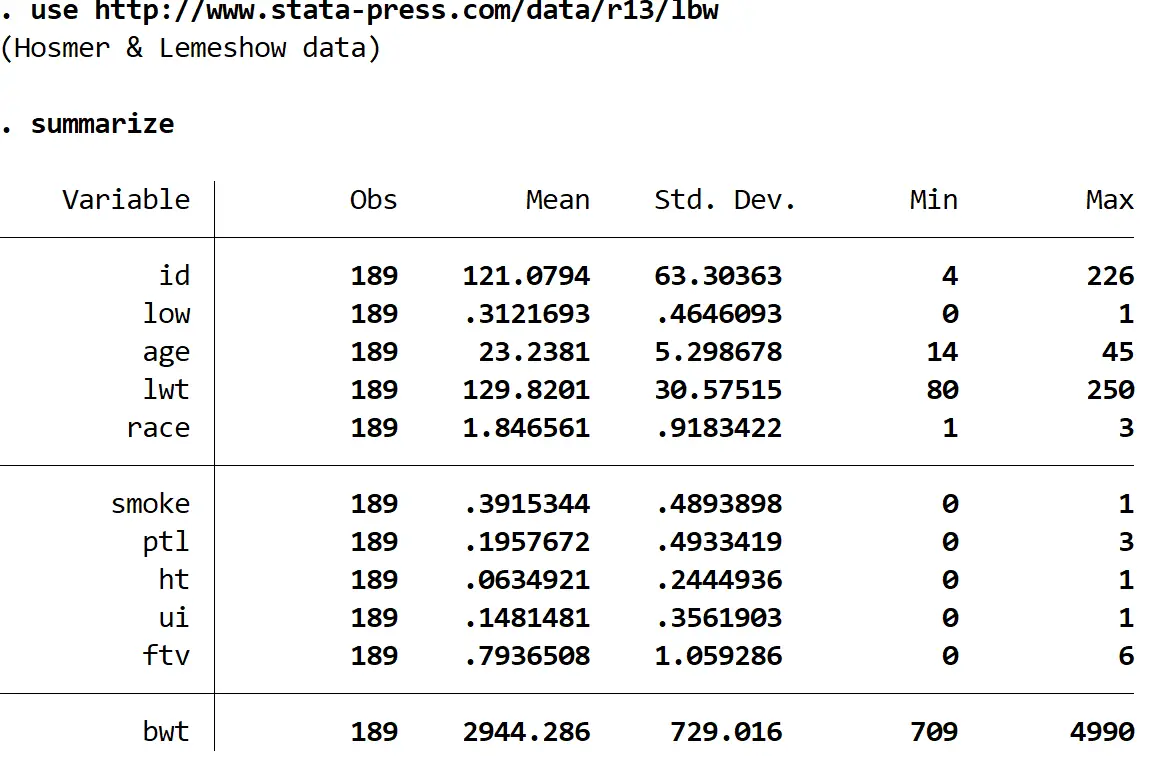
我们可以看到数据集中有 11 个不同的变量，但我们感兴趣的只有三个：

• 低——婴儿出生体重是否低。 1 = 是，0 = 否。
• 年龄——母亲的年龄。
• 吸烟——母亲在怀孕期间是否吸烟。 1 = 是，0 = 否。

步骤 3：执行逻辑回归。

在命令框中键入以下内容，以使用年龄和烟雾作为解释变量并使用低作为响应变量来执行逻辑回归。

低年龄烟雾 Logit

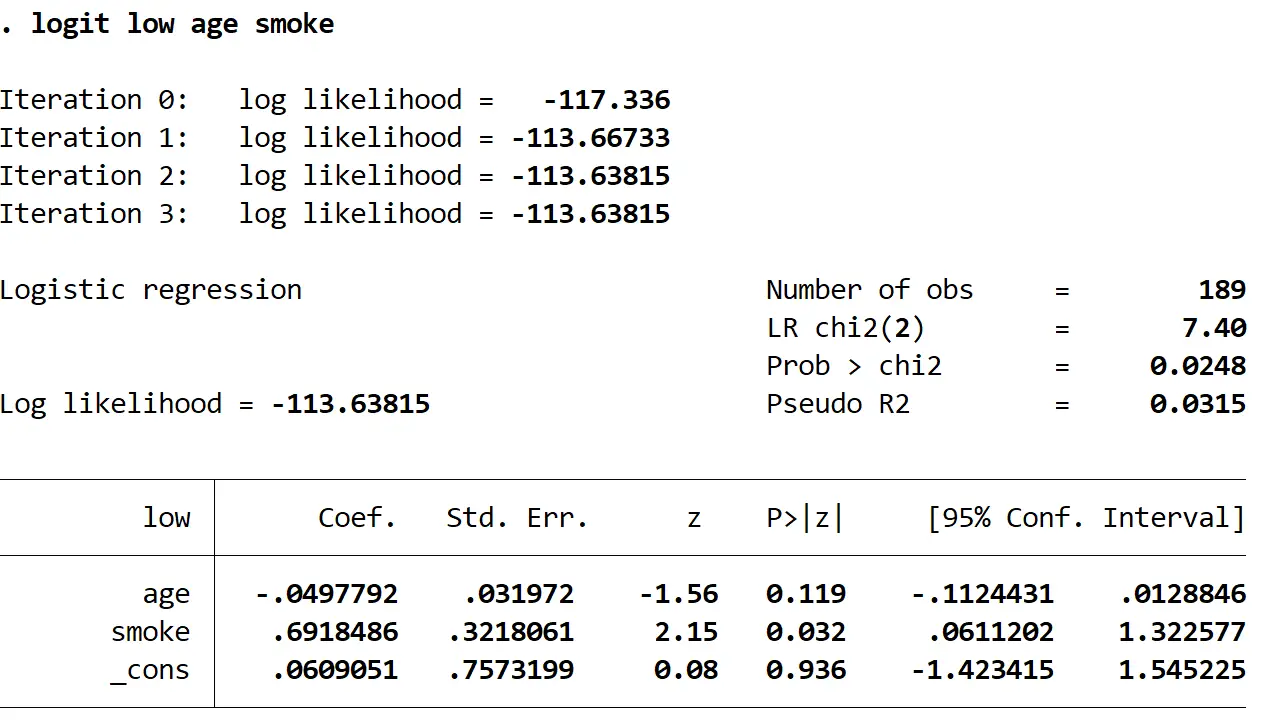
以下是如何解释结果中最有趣的数字：

系数（年龄）： -.0497792。保持烟雾不变，年龄每增加一年，婴儿出生体重过低的几率就会增加 exp(-0.0497792) = 0.951。这个数字小于 1 意味着年龄的增加实际上与低出生体重婴儿的几率降低有关。

例如，假设母亲 A 和母亲 B 都吸烟。如果母亲A比母亲B大一岁，那么母亲A生出低体重儿的几率仅为母亲B生出低体重儿的几率的95.1%。诞生。

P>|z| （年龄）： 0.119。这是与年龄检验统计量相关的 p 值。由于该值不小于 0.05，因此年龄并不是低出生体重的统计显着预测因素。

优势比（烟雾）： 0.6918486。在年龄不变的情况下，怀孕期间吸烟的母亲比怀孕期间不吸烟的母亲生出低出生体重婴儿的概率 exp(.6918486) = 1.997 更高。

例如，假设母亲 A 和母亲 B 都是 30 岁。如果母亲A在怀孕期间吸烟，而母亲B不吸烟，那么母亲A生出低体重儿的几率比母亲B生出低体重儿的几率高99.7%。

P>|z| （烟）： 0.032。这是与烟雾检验统计量相关的 p 值。由于该值小于 0.05，因此吸烟是低出生体重的统计显着预测因子。

第四步：报告结果。

最后，我们想报告逻辑回归的结果。以下是如何执行此操作的示例：

进行逻辑回归以确定母亲的年龄和吸烟习惯是否影响生出低出生体重婴儿的可能性。分析中使用了 189 名母亲的样本。

结果显示，吸烟与低出生体重的可能性之间存在统计显着关系（z = 2.15，p = 0.032），而年龄与低出生体重的可能性之间不存在统计显着关系（z = -1.56） ，p = 0.032）。 119）。