如何在 r 中执行 dunnett 检验

事后检验是在方差分析之后执行的一种检验，用于确定哪些组平均值在统计上彼此显着不同。

如果其中一个研究组被视为对照组，那么我们应该使用Dunnett 检验作为事后检验。

本教程介绍如何在 R 中执行 Dunnett 检验。

示例：R 中的 Dunnett 测试

假设一位老师想知道两种新的学习技巧是否有可能提高学生的考试成绩。为了测试这一点，她将班上 30 名学生随机分为以下三组：

• 对照组：10名学生
• 新技术学习1：10名学生
• 新技术学习2：10名学生

在使用指定的学习技巧一周后，每个学生都会参加相同的考试。

我们可以使用 R 中的以下步骤创建数据集，可视化组均值，执行单向方差分析，最后执行 Dunnett 检验，以确定哪种新研究技术（如果有）与对照组相比会产生不同的结果。

步骤 1：创建数据集。

以下代码演示了如何创建包含所有 30 名学生的考试结果的数据集：

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

第 2 步：查看每组的考试结果。

以下代码显示如何生成箱线图以可视化每组考试结果的分布：

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

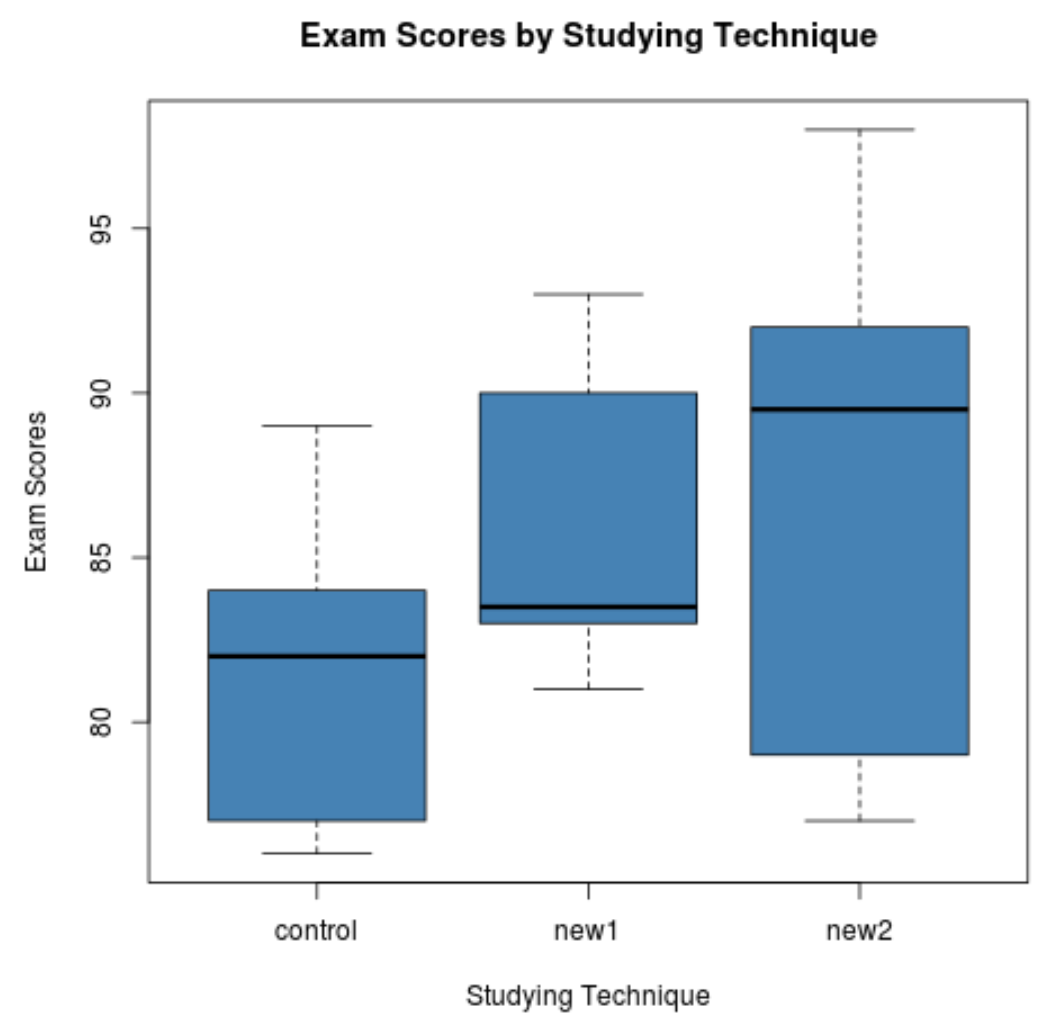
仅从箱线图中，我们就可以看到每种学习技术的考试成绩分布都非常不同。然后，我们将执行单向方差分析以确定这些差异是否具有统计显着性。

相关：如何在 R 中的单个图表中绘制多个箱线图

步骤 3：执行单向方差分析。

以下代码显示如何执行单向方差分析来测试每组平均考试成绩之间的差异：

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

由于总体 p 值 ( 0.0476 ) 小于 0.05，这表明每个组的平均考试成绩不同。接下来，我们将执行 Dunnett 测试，以确定哪种学习方法产生的平均考试分数与对照组的分数不同。

步骤 4：执行 Dunnett 检验。

要在 R 中执行 Dunnett 测试，我们可以使用DescTools库中的DunnettTest()函数，该函数使用以下语法：

邓尼特检验(x, g)

金子：

• x：数据值的数值向量（例如考试成绩）
• g：指定组名称的向量（例如研究技术）

以下代码展示了如何在我们的示例中使用此函数：

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

结果解释方式如下：

• 新学习方法 1 和对照组之间的考试成绩平均差异为4.2。相应的 p 值为0.1787 。
• 新学习方法2与对照组的考试成绩平均差异为6.4。相应的 p 值为0.0296 。

根据结果，我们可以看到，学习技术 2 是唯一产生与对照组显着不同 (p = 0.0296) 的平均考试成绩的技术。

其他资源

单向方差分析简介
如何在 R 中执行单向方差分析
如何在 R 中执行 Tukey 测试