如何在 excel 中执行部分 f 检验
部分 F 检验用于确定回归模型与同一模型的嵌套版本之间是否存在统计显着差异。
嵌套模型只是在整体回归模型中包含预测变量子集的模型。
例如，假设我们有以下具有四个预测变量的回归模型：
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
嵌套模型的一个示例是以下仅包含两个原始预测变量的模型：
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
为了确定这两个模型是否显着不同，我们可以执行部分 F 检验，计算以下 F 检验统计量：
F = ((缩减RSS –完整RSS)/p) / (完整RSS /nk)
金子：
- 简化的RSS ：简化（即“嵌套”）模型的残差平方和。
- RSS full ：完整模型的残差平方和。
- p：从完整模型中删除的预测变量的数量。
- n：数据集中的观测总数。
- k：完整模型中的系数数量（包括截距）。
该检验使用以下原假设和备择假设：
H 0 ：从完整模型中删除的所有系数均为零。
H A ：从完整模型中删除的至少一个系数是非零的。
如果与 F 检验统计量对应的p 值低于某一显着性水平（例如 0.05），则我们可以拒绝零假设并得出结论：从完整模型中删除的至少一个系数是显着的。
以下示例显示如何在 Excel 中执行部分 F 检验。
示例：Excel 中的部分 F 检验
假设我们在Excel中有以下数据集：
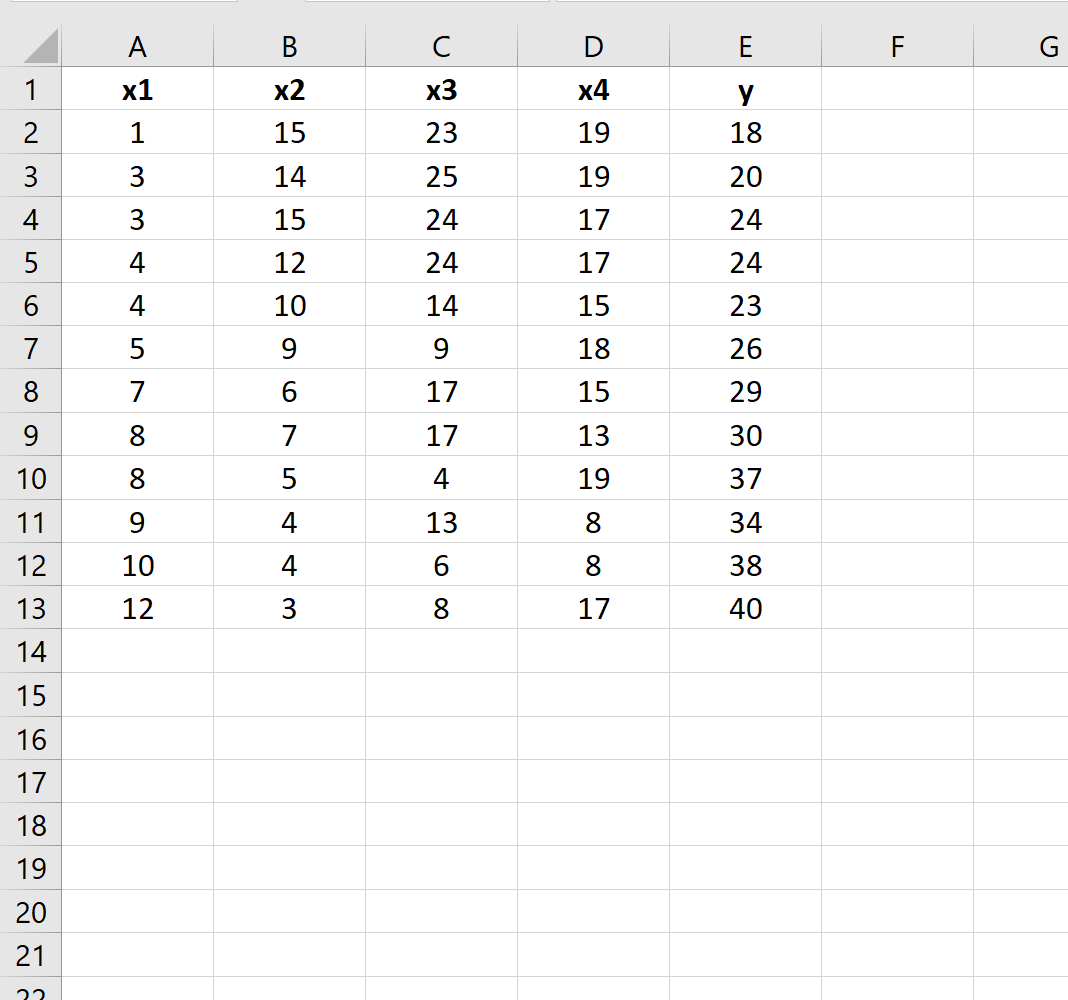
假设我们想要确定以下两个回归模型之间是否存在差异：
完整模型： y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
简化模型： y = β 0 + β 1 x 1 + β 2 x 2
我们可以在Excel中对每个模型进行多元线性回归，得到以下结果：
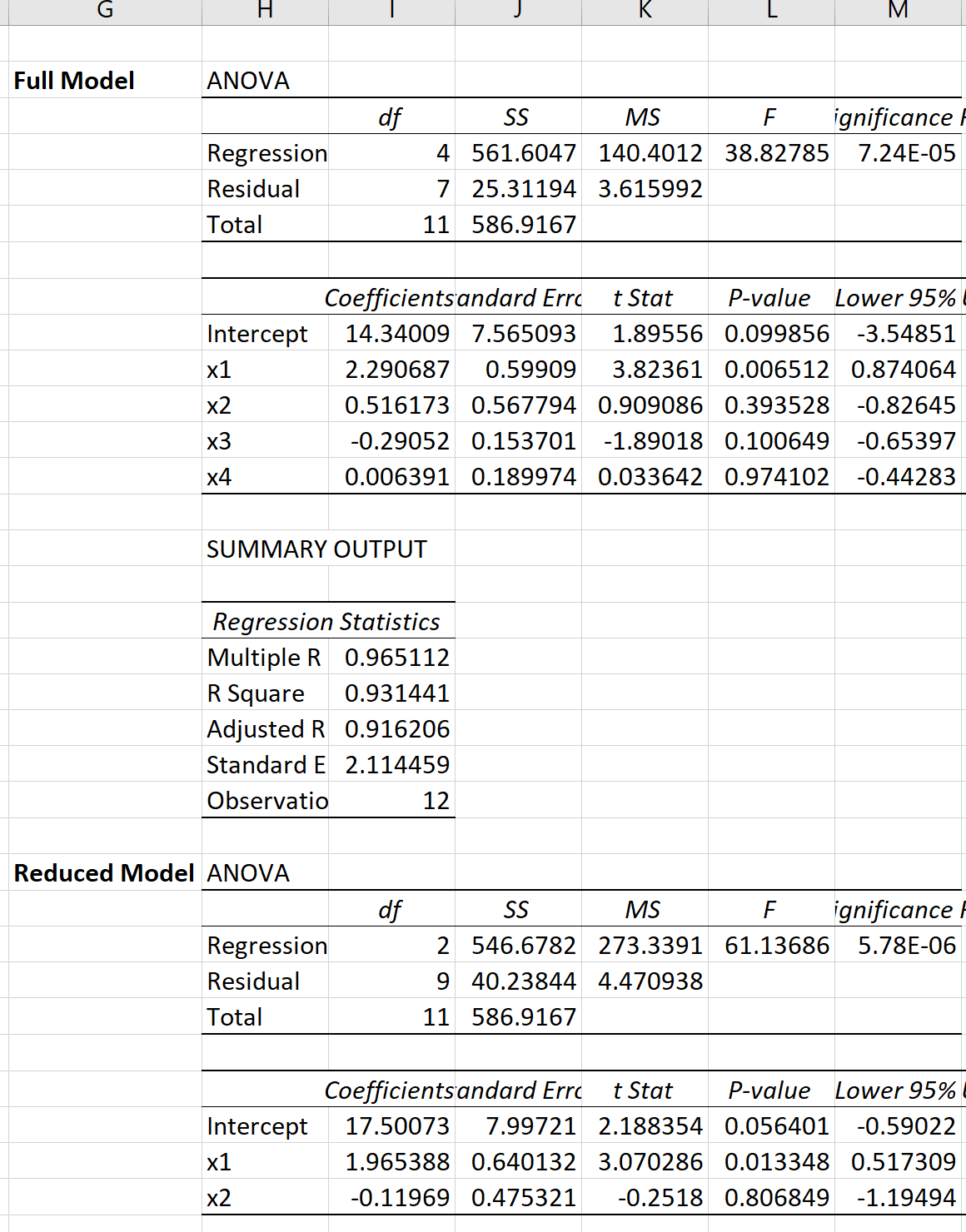
然后我们可以使用以下公式来计算部分 F 检验的 F 检验统计量：
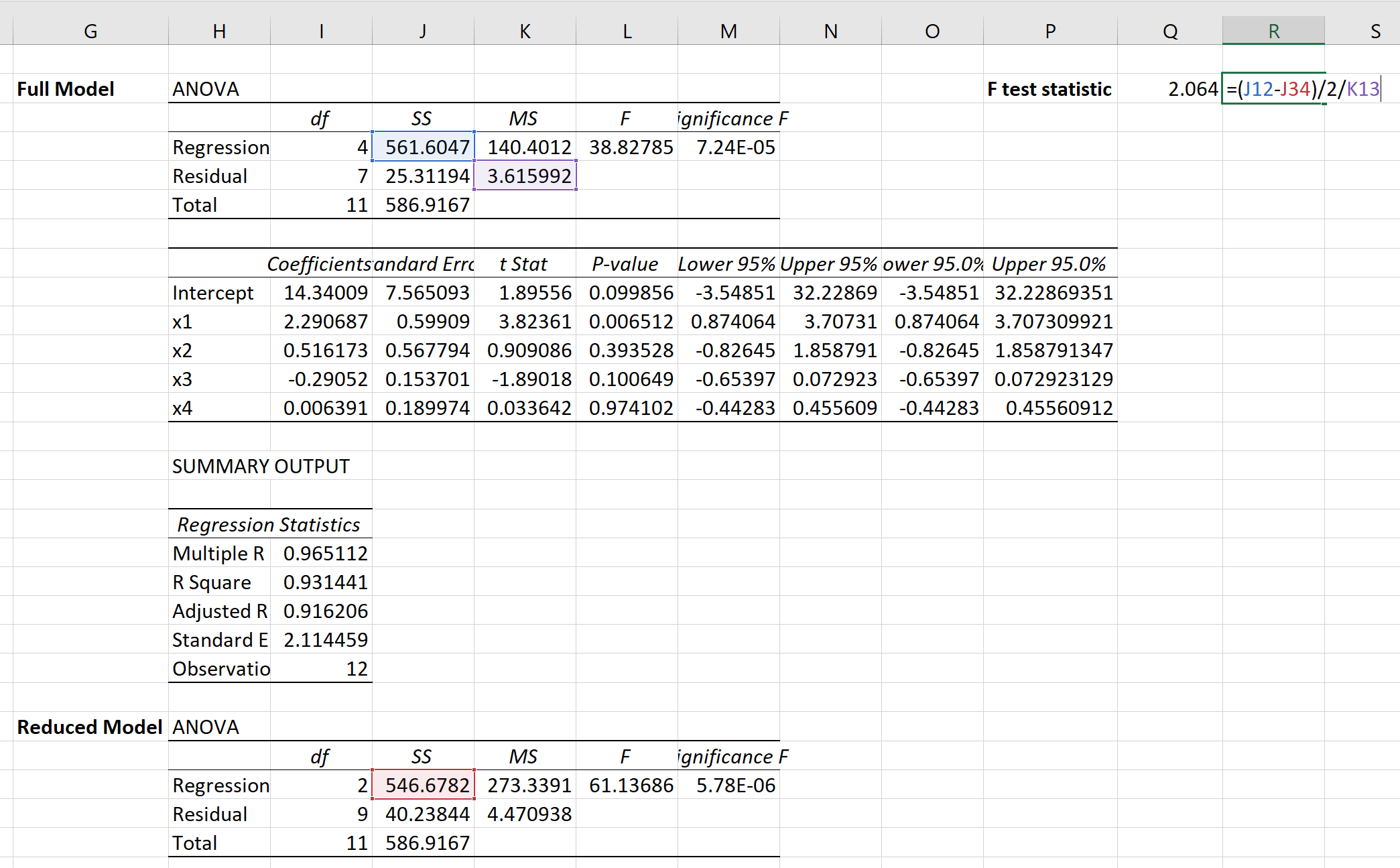
检验统计量结果为2.064 。
然后我们可以使用以下公式来计算相应的 p 值：
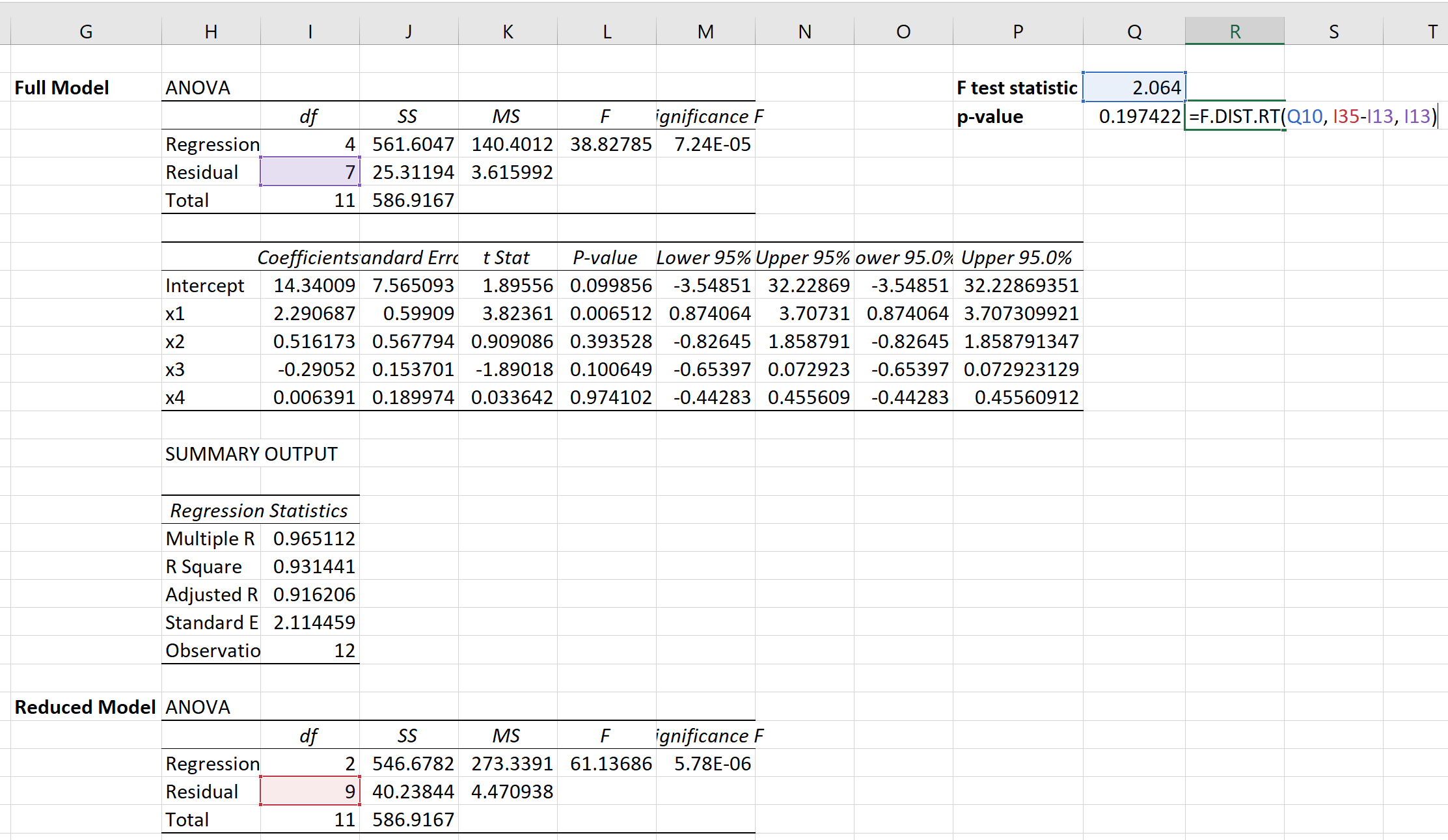
p 值为0.1974 。
由于该 p 值不小于 0.05，因此我们将无法拒绝原假设。这意味着我们没有足够的证据表明x3或x4预测变量具有统计显着性。
换句话说，将x3和x4添加到回归模型中并不会显着改善模型拟合度。
其他资源
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多