配对或未配对 t 检验:有什么区别?
在统计学中,有两种类型的双样本 t 检验:
配对 t 检验:当一个样本中的每个个体也出现在另一个样本中时,用于比较两个样本的平均值。
未配对 t 检验:当一个样本中的每个个体独立于另一个样本中的每个个体时,用于比较两个样本的均值。
注意:不配对 t 检验更常称为独立样本 t 检验。
例如,假设一位教授想要确定两种不同的学习技巧是否会导致不同的平均考试成绩。
为了进行配对 t 检验,他可以招募 10 名学生,让他们使用一种学习技巧一个月并参加考试,然后让他们使用第二种学习技巧一个月并参加另一场同等难度的考试。
数据如下所示:
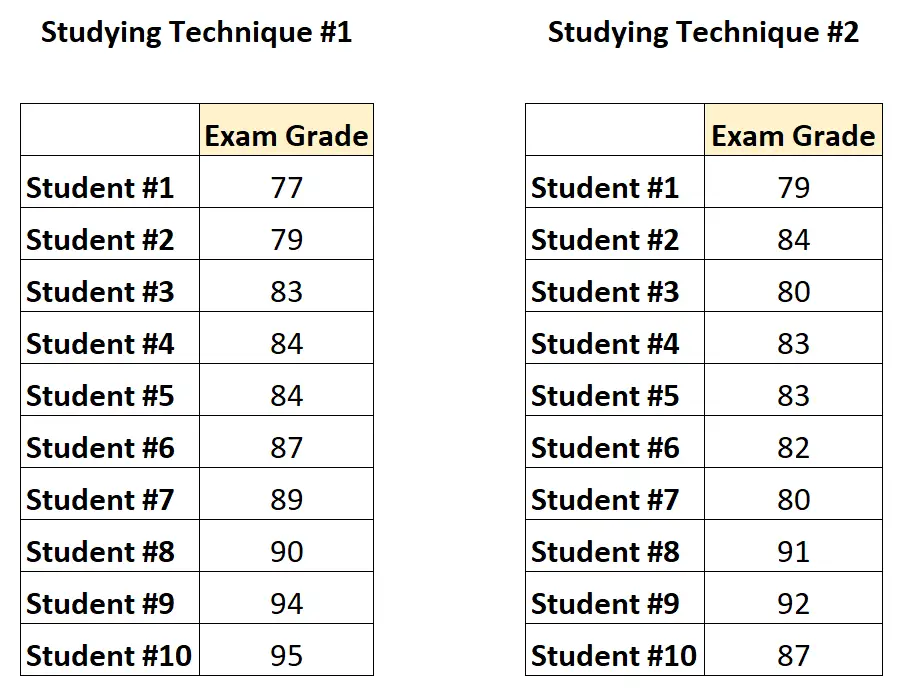
由于每个学生都出现在每个组中,教授将进行配对 t 检验,以确定两组之间的平均分数是否不同。
为了进行不配对的 t 检验,他可以总共招募 20 名学生,并将他们随机分为两组,每组 10 人。他可以要求一组使用一种学习技巧一个月,另一组“使用第二种学习技巧一个月”。一个月。月并让所有学生参加相同的考试。
数据如下所示:
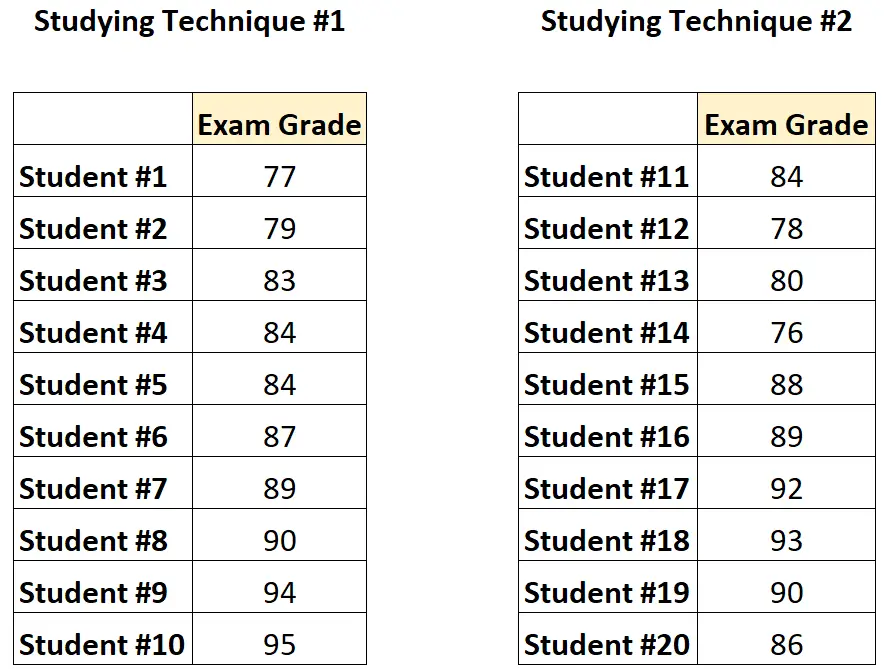
由于一组中的学生完全独立于另一组中的学生,因此教授将进行不配对的 t 检验来确定两组之间的平均分数是否不同。
假设
配对和非配对 t 检验均做出以下假设:
- 两个样本的数据均采用随机抽样方法获得。
- 两个样本的数据应近似呈正态分布。
- 两个样本中不应存在极端异常值。
在执行任何 t 检验之前应验证这些假设,以确保测试结果的可靠性。
的优点和缺点
配对 t 检验具有以下优点:
- 需要较小的样本。请注意,上一示例中的配对 t 检验总共只需要 10 名学生,而未配对 t 检验总共需要 20 名学生。
- 每个样本都包含具有相同特征的个体。这两个群体都保证有具有能力、智力等的个人。平等,因为每个组中出现相同的个体。
然而,配对 t 检验具有以下潜在缺点:
- 减少样本量的潜力。如果某人退出研究,则每组的样本量都会减少一个,因为该人出现在每组中。
- 秩序效应的潜力。顺序效应是指由于向个体提供治疗的顺序而导致的两组之间结果的差异。例如,一个人在第二次考试中表现更好可能只是因为他们提高了应试技巧,而不是因为他们的学习技巧。
在决定是否使用配对或不配对 t 检验时,请记住这些优点和缺点。
其他资源
查看以下教程以更好地理解配对 t 检验:
并使用以下教程更好地理解不配对 t 检验(又名独立样本 t 检验):