配对样本 t 检验：定义、公式和示例

当一个样本中的每个观察值可以与另一个样本中的观察值相关联时，配对样本 t 检验用于比较两个样本的平均值。

本教程解释了以下内容：

• 执行配对样本 t 检验的动机。
• 用于执行配对样本 t 检验的公式。
• 执行配对样本 t 检验必须满足的假设。
• 如何执行配对样本 t 检验的示例。

配对样本 t 检验：动机

配对样本 t 检验通常用于两种情况：

1. 在治疗前后对受试者进行测量——例如，在参加训练计划之前和之后测量大学篮球运动员的最大垂直弹跳。

2. 在两种不同条件下进行测量– 例如，使用两种不同药物测量患者的反应时间。

在这两种情况下，我们想要比较两组之间的平均测量值，其中一个样本的每个观察结果都可以与另一个样本的观察结果相关联。

配对样本 t 检验：公式

配对样本 t 检验始终使用以下原假设：

• H ₀ : μ ₁ = μ ₂ （两个总体平均值相等）

备择假设可以是双边的、左的或右的：

• H ₁ （双尾）： μ ₁ ≠ μ ₂ （两个总体的均值不相等）
• H ₁ （左）： μ ₁ < μ ₂ （总体 1 的平均值低于总体 2 的平均值）
• H ₁ （右）： μ ₁ > μ ₂ （总体 1 的平均值大于总体 2 的平均值）

我们使用以下公式来计算 t 检验统计量：

t = x_差异/ (s_差异/√n)

金子：

• x _diff ：差异平均值示例
• s：差异标准差示例
• n：样本大小（即对的数量）

如果与具有 (n-1) 个自由度的 t 检验统计量相对应的 p 值小于所选的显着性水平（常见选择为 0.10、0.05 和 0.01），则您可以拒绝原假设。

配对样本 t 检验：假设

为了使配对样本 t 检验的结果有效，必须满足以下假设：

• 参与者应从人群中随机选择。
• 对之间的差异应近似呈正态分布。
• 差异中不应存在极端异常值。

配对样本 t 检验：示例

假设我们想知道某个训练计划是否能够提高大学篮球运动员的最大垂直弹跳（以英寸为单位）。

为了测试这一点，我们可以招募 20 名大学篮球运动员作为简单的随机样本，并测量他们每个人的最大垂直弹跳。然后我们可以让每个球员使用一个月的训练计划，然后在月底再次测量他们的最大垂直弹跳。

为了确定训练计划是否确实对最大垂直弹跳产生影响，我们将使用以下步骤在 α = 0.05 显着性水平上执行配对样本 t 检验：

步骤 1：计算差异的汇总数据。

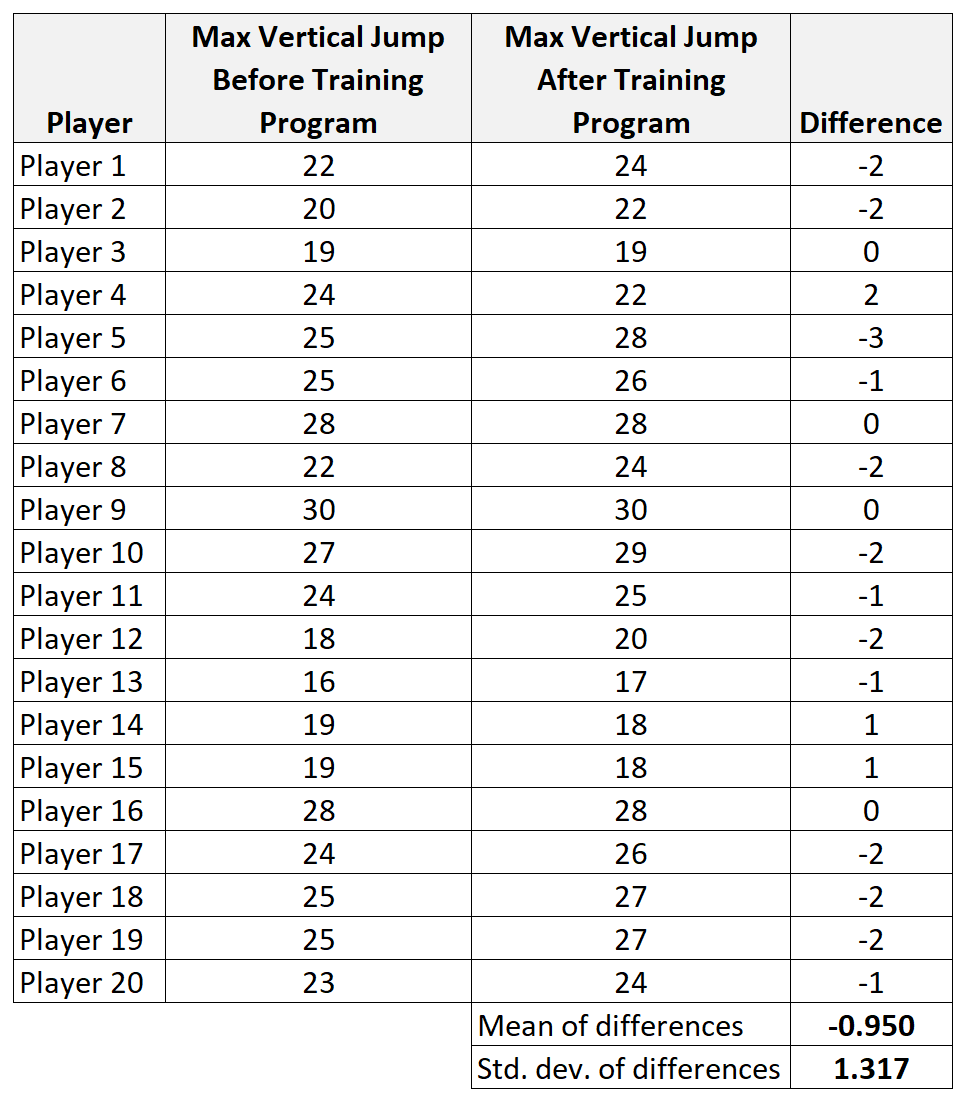
• x _diff ：样本差异平均值 = -0.95
• s：差异的样本标准差 = 1.317
• n：样本大小（即对数）= 20

第 2 步：定义假设。

我们将使用以下假设对配对样本进行 t 检验：

• H ₀ : μ ₁ = μ ₂ （两个总体平均值相等）
• H ₁ : μ ₁ ≠ μ ₂ （两个总体平均值不相等）

步骤 3：计算t检验统计量。

t = x_差异/ (s_差异/√n) = -0.95 / (1.317/ √ 20) = -3.226

步骤 4：计算t检验统计量的 p 值。

根据T 分数到 P 值计算器，与 t = -3.226 和自由度 = n-1 = 20-1 = 19 相关的 p 值为0.00445 。

第五步：得出结论。

由于该 p 值低于显着性水平 α = 0.05，因此我们拒绝原假设。我们有足够的证据表明，球员在参加训练计划之前和之后的平均最大垂直弹跳是不同的。

注意：您还可以通过简单地使用 配对样本 t 检验计算器来执行整个配对样本 t 检验。

其他资源

以下教程解释了如何使用不同的统计程序执行配对样本 t 检验：

如何在 Excel 中执行配对样本 t 检验
如何在 SPSS 中执行配对样本 t 检验
如何在 Stata 中进行配对样本 t 检验
如何在 TI-84 计算器上执行配对样本 t 检验
如何在 R 中执行配对样本 t 检验
如何在 Python 中执行配对样本 t 检验
如何手动执行配对样本 T 检验