什么是零阶相关？

在统计学中，两个变量之间的相关性告诉我们这两个变量之间的关系。

最基本的相关类型之一称为零阶相关，它是指在不控制其他变量可能影响的情况下两个变量之间的相关。

这种相关性的一个例子是皮尔逊相关系数，它衡量两个变量之间的线性关联，可以取 -1 到 1 之间的值，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

相关性距离零越远，两个变量之间的关联性越强。

一阶和二阶相关性

如果我们计算两个变量 A 和 B 之间的相关性，同时控制第三个变量 C 的影响，我们将 A 和 B 之间的相关性称为一阶相关性。

类似地，如果我们计算两个变量 A 和 B 之间的相关性，同时控制变量 C 和 D 的影响，我们可以将 A 和 B 之间的相关性称为二阶相关性。

零阶相关示例

假设我们有以下数据集，显示 10 名不同学生的学习时间和考试成绩：

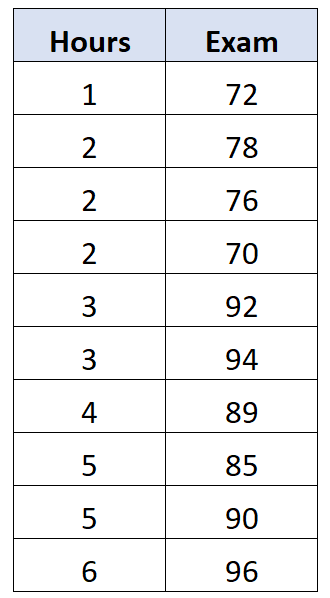
事实证明，这两个变量之间的相关性为0.762 。这将被视为两个变量之间的零阶相关性，因为我们不控制第三个变量的潜在影响。

然而，实际上，其他因素可能会影响这两个变量之间的关系。

例如，学生当前在班级中的成绩可能会影响他们的考试成绩。假设我们也可以访问这些数据：

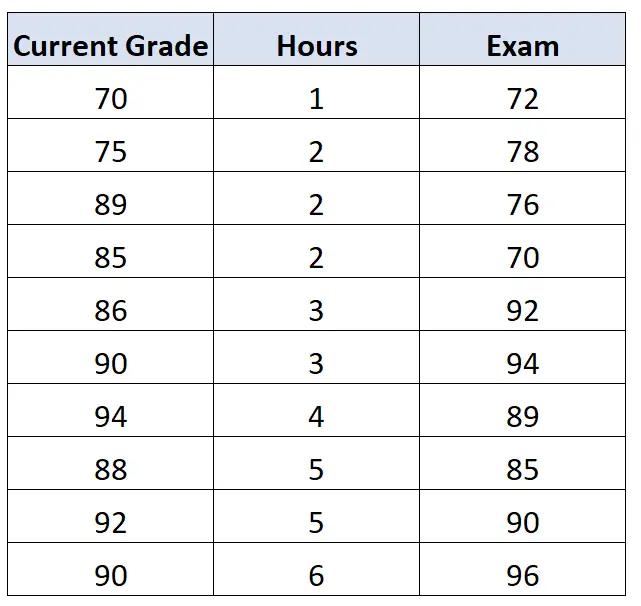
如果我们在控制当前成绩的影响的情况下计算学时和考试之间的相关性，我们会发现学时和考试之间的一阶相关性是0.578 。

这意味着即使在控制了学生当前班级成绩的影响之后，学习时间和考试成绩之间仍然存在相当强的正相关性。

注意：一阶相关有时称为偏相关。本教程介绍如何在 Excel 中计算偏相关。

相关矩阵中的零阶相关

我们创建一个相关矩阵，每当对于一组变量时，矩阵中显示的相关系数始终是零阶相关，因为它们只是变量的每个成对组合之间的相关性，而不考虑其他变量的影响。

例如，考虑上一个示例中的数据集：

如果我们为此数据集创建一个相关矩阵，它将如下所示：

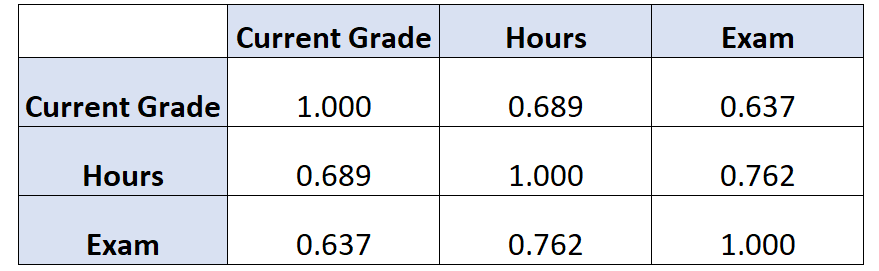
对此的解释方法是：

• 当前成绩与学习时间之间的相关性为0.689 。
• 当前分数与考试分数之间的相关性为0.637 。
• 学习时间和考试成绩之间的相关性为0.762 。

这些相关性中的每一个都是零阶相关性。

其他资源

以下教程提供有关相关系数的其他信息：

皮尔逊相关系数简介
如何读取相关矩阵
如何在Excel中计算偏相关