统计学中的预测误差是什么？ （定义和示例）
在统计学中，预测误差是指某些模型预测的值与实际值之间的差异。
预测误差通常在两种情况下使用：
1.线性回归：用于预测连续响应变量的值。
我们通常使用RMSE（均方根误差）指标来测量线性回归模型的预测误差。
计算方法如下：
RMSE = √ Σ(ŷ i – y i ) 2 / n
金子：
- Σ是一个符号，意思是“和”
- ŷ i是第 i个观测值的预测值
- y i是第 i 个观测值的观测值
- n 是样本量
2.逻辑回归：用于预测二元响应变量的值。
衡量逻辑回归模型预测误差的常见方法是使用称为总分类错误率的指标。
计算方法如下：
总误分类率 = (# 错误预测 / # 总预测)
误分类率的值越低，模型能够更好地预测响应变量的结果。
以下示例展示了如何在实践中计算线性回归模型和逻辑回归模型的预测误差。
示例 1：计算线性回归中的预测误差
假设我们使用回归模型来预测 10 名球员在一场篮球比赛中会得分多少分。
下表显示了模型预测的得分与球员实际得分的比较：
我们将计算均方根误差 (RMSE)，如下所示：
- RMSE = √ Σ(ŷ i – y i ) 2 / n
- RMSE = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10)
- 均方根误差 = 4
均方误差为4。这告诉我们预测得分与实际得分之间的平均偏差为 4。
示例 2：计算逻辑回归中的预测误差
假设我们使用逻辑回归模型来预测 10 名大学篮球运动员是否会被选入 NBA。
下表显示了每位球员的预测结果与实际结果（1 = 选秀，0 = 落选）：
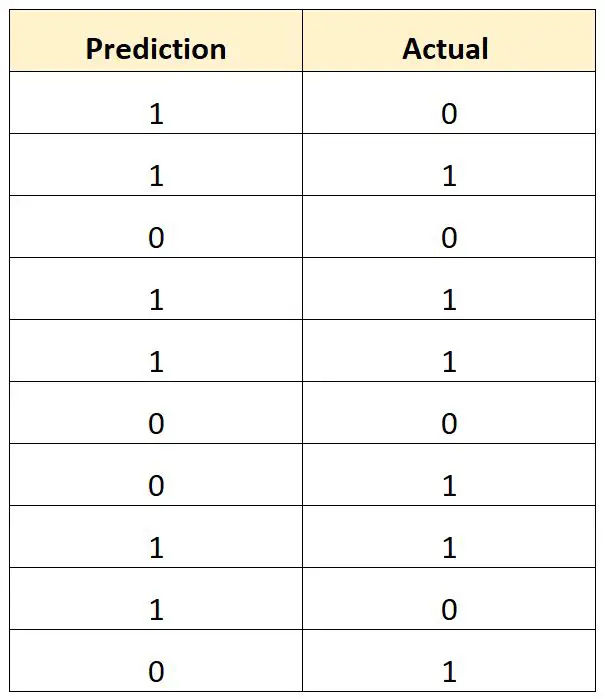
我们将计算总错误分类率如下：
- 总误分类率 = (# 错误预测 / # 总预测)
- 总分类错误率 = 4/10
- 总误分类率 = 40%
总分类错误率为40% 。
这个值相当高，表明该模型不能很好地预测球员是否会被选中。
其他资源
以下教程介绍了不同类型的回归方法：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多