频率多边形

本文解释了什么是频数多边形以及它的用途。此外，您还将了解什么是不同类型的频率多边形以及每种频率多边形的示例。

什么是频数多边形？

频数多边形是一种统计图，其中数据集由点表示并由线连接。

在统计学中，通常使用频数多边形来表示时间序列。因为这种类型的图表对于分析数据的演变非常有用。

频数多边形可以通过连接条形图或直方图的条形末端来制作。下面我们将看到这是如何完成的。

如何创建频率多边形

创建频数多边形的步骤如下：

1. 绘制频率多边形的水平轴和垂直轴并创建比例，以便您可以在图表上表示数据。
2. 将数据对表示为图表上的点。
3. 使用直线连接图表上的连续点。

频数多边形示例

为了让您可以准确地了解如何构建频率多边形，下面是一个解释的示例。

• 以下数据表汇总了一家上市公司过去 10 年的股票价值。使用频率多边形绘制数据图。

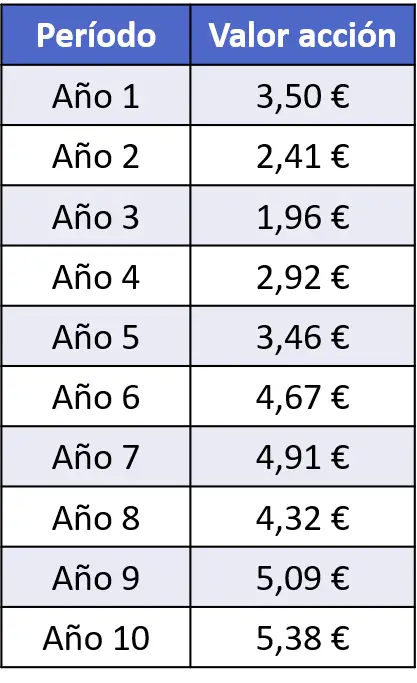
首先，我们必须表示频率多边形的轴。我们将在横轴上放置周期，在纵轴上放置股票价格：

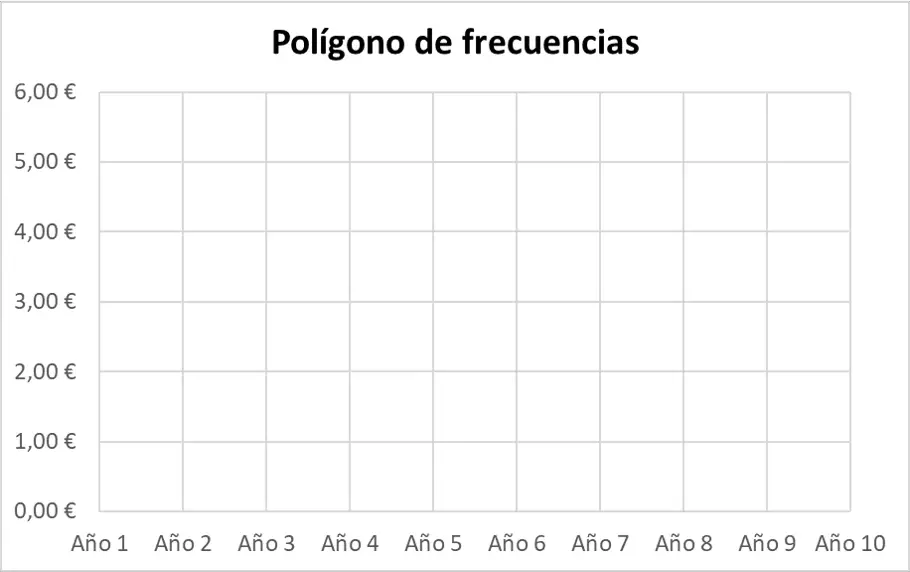
其次，我们用点表示统计数据集。请记住，每个点都表示在图表上，其中轴上相应值的两条假想线相交。

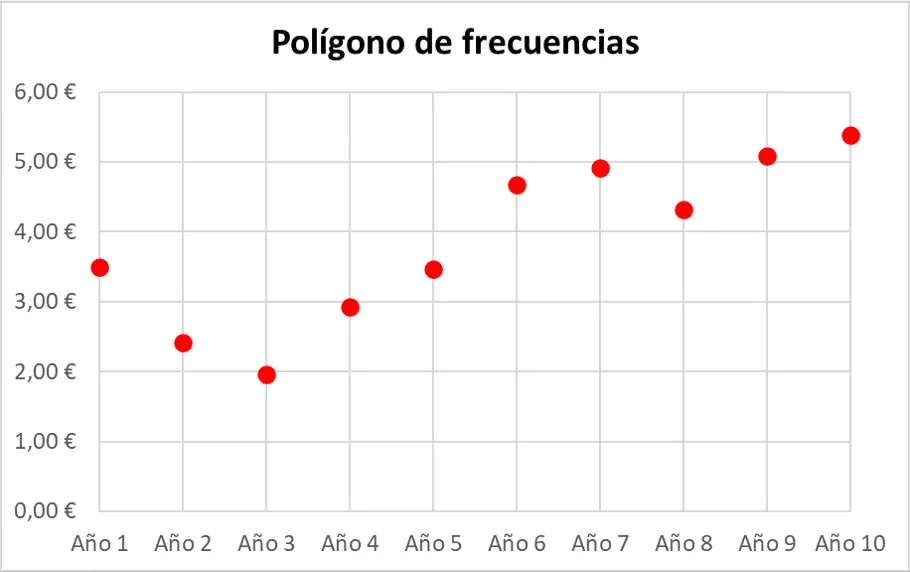
最后，简单地用直线连接连续的点，形成整个频率多边形的连续线。

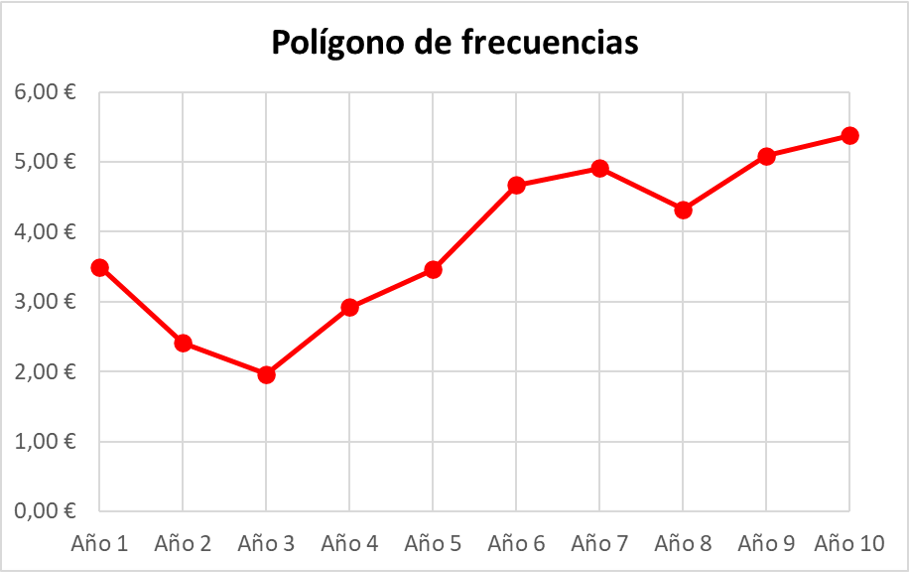
在这种情况下，绝对频率在频率多边形中表示，但也可以表示相对（或百分比）频率。

分组数据的频率多边形

我们刚刚看到了当变量是离散的时候如何制作频数多边形，但是连续变量也可以制作频数多边形，也就是说当数据被分组为区间时。您可以在下面看到一个已解决的此类示例。

• 测量了50人的样本量，并将数据记录在下面的频率表中。使用频率多边形绘制数据图。

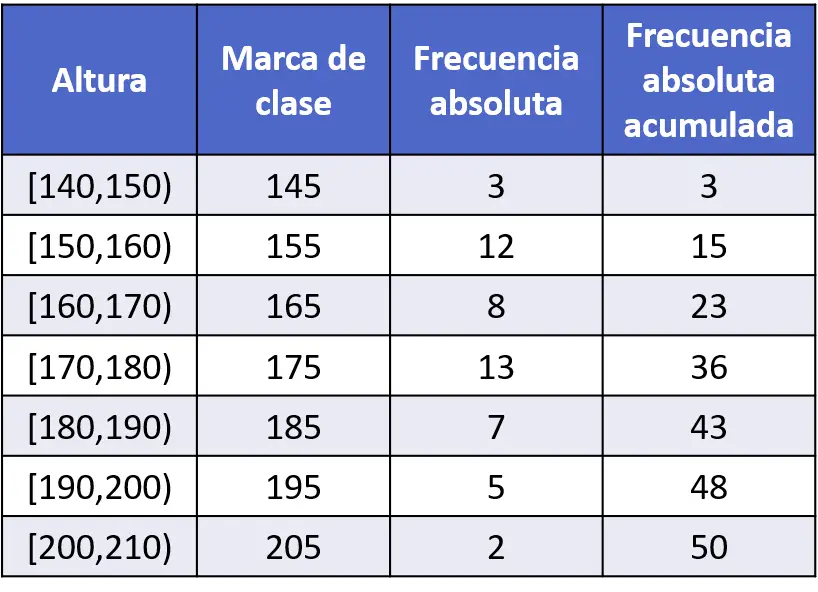
由于数据是按区间分组的，因此频数多边形的点应绘制在每个区间的类标记处，即区间端点的中点处。

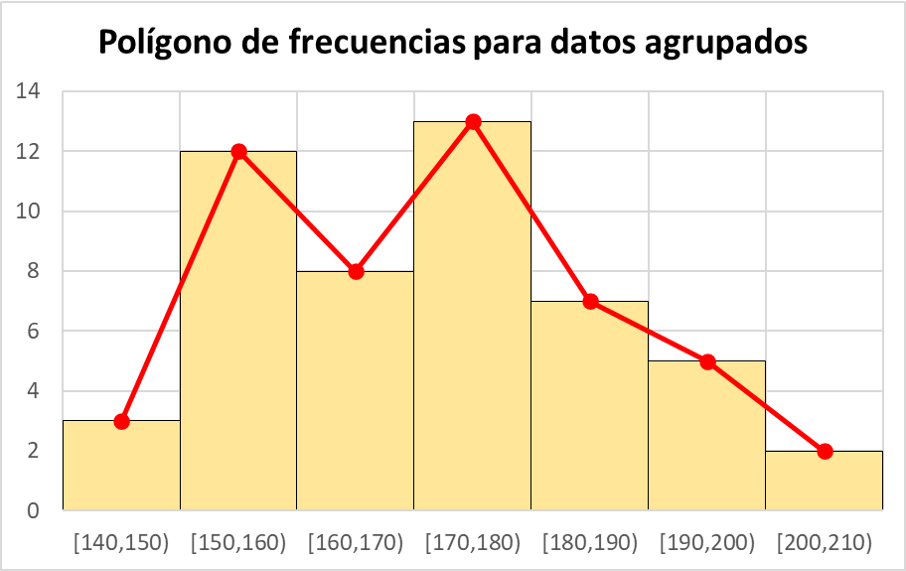
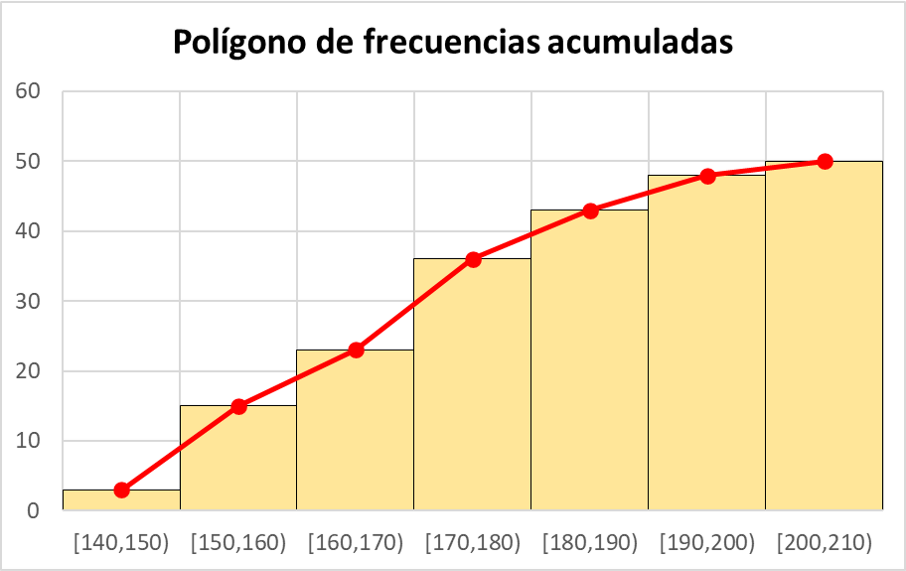
如图所示，当数据分组时，频数多边形可以与直方图结合起来。事实上，如果先制作直方图，则要绘制频数多边形，只需将直方图中每个矩形条的中点连接起来即可。

累积频数多边形

在统计学中，频数多边形也用来表示累积频率。只需先计算数据集的累积频率，然后使用累积频率而不是绝对频率来表示频数多边形中的点。

请记住，累积绝对频率是通过将所有先前的绝对频率加上间隔本身的绝对频率来计算的。

例如，您可以从下面的上一个练习的数据集中看到累积绝对频率多边形：