什么是食品测试？ （解释和示例）

Chow检验是由经济学家Gregory Chow开发的统计检验，用于检验不同数据集上两个不同回归模型的系数是否相等。

Chow 检验通常用于计量经济学领域的时间序列数据，以确定给定时间点的数据是否存在结构性断裂。

例如，考虑以下散点图：

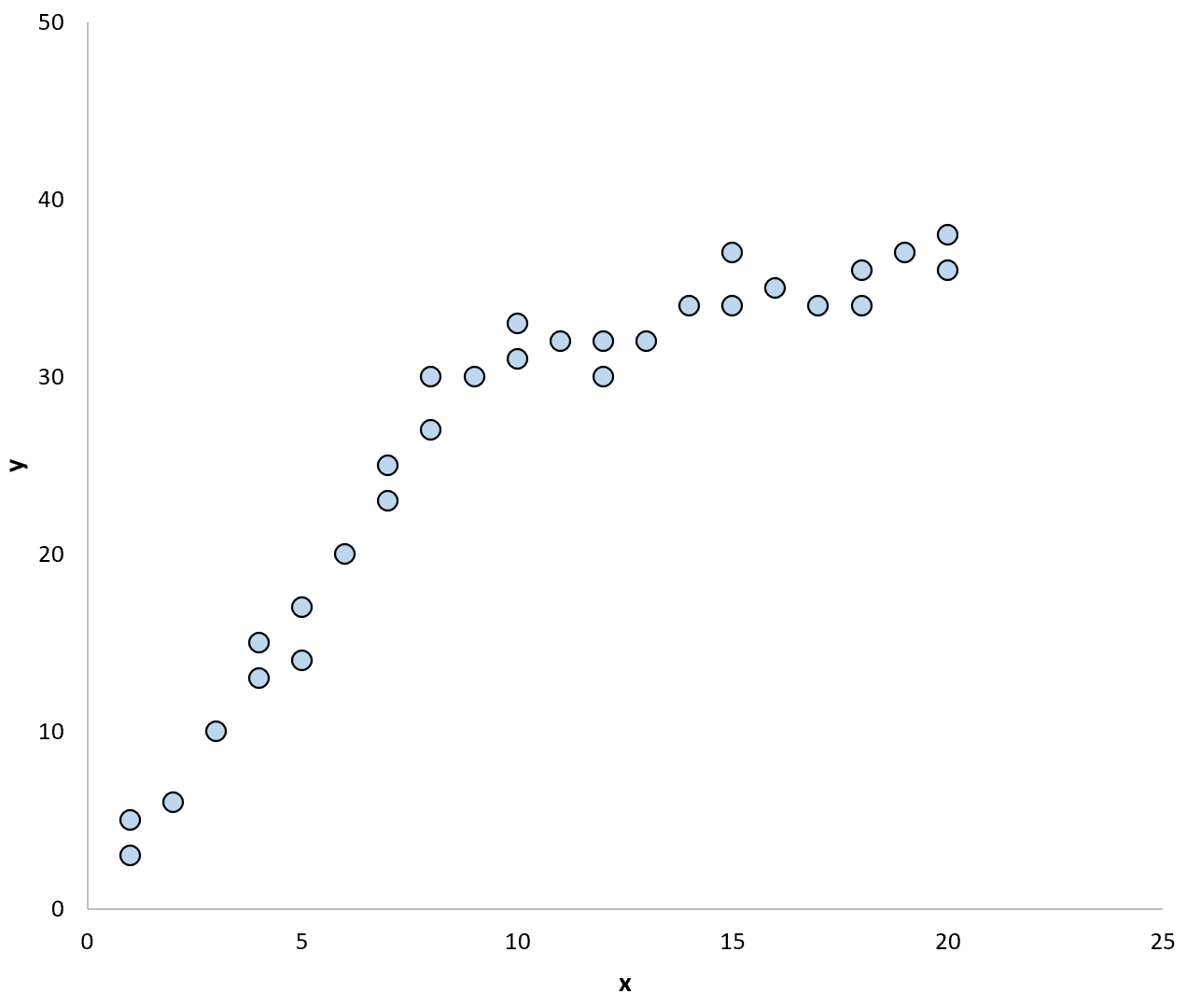
如果我们使用回归线来总结数据中的模型，它可能如下所示：

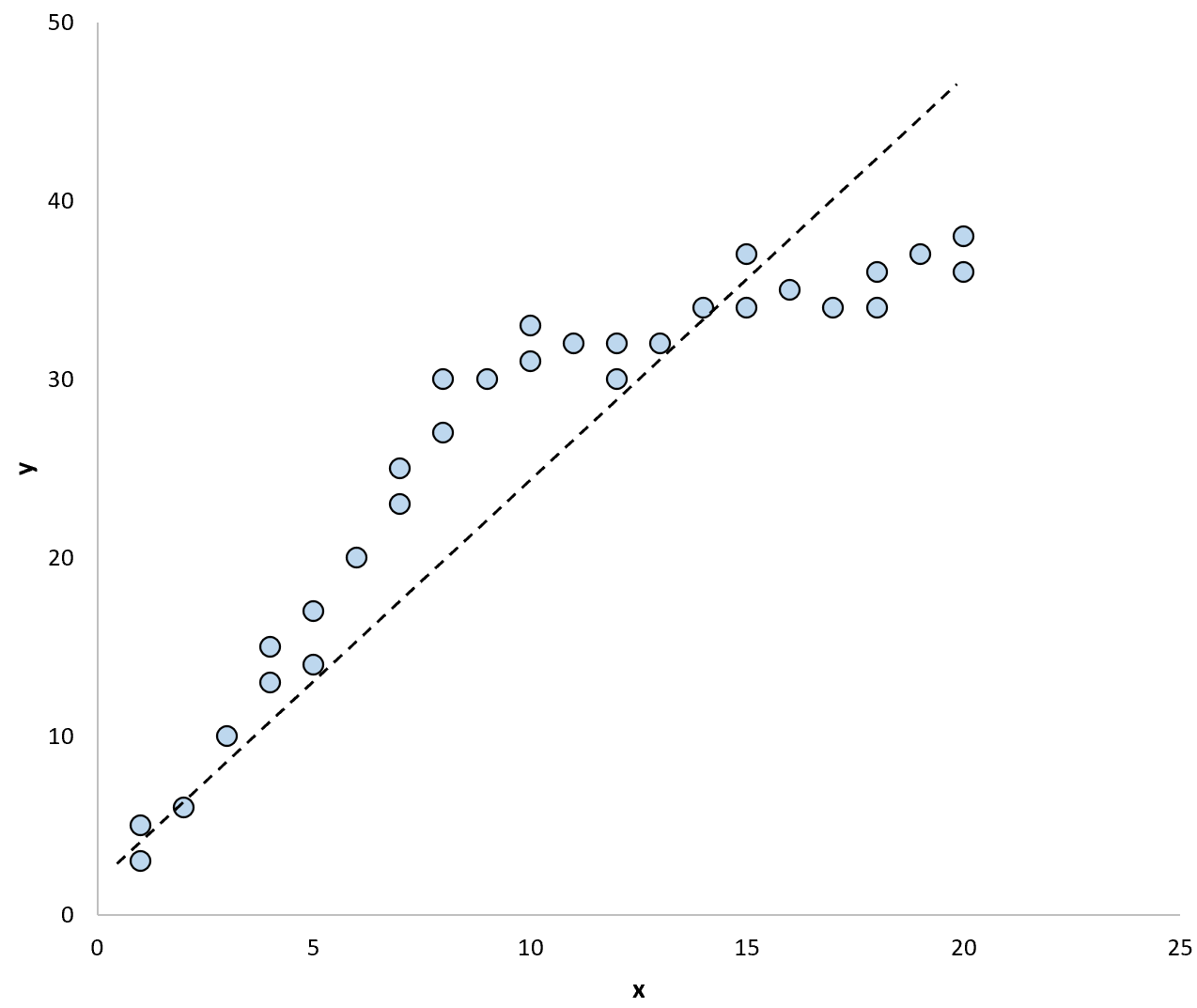
如果我们使用两条单独的回归线来总结数据中的模型，它可能如下所示：

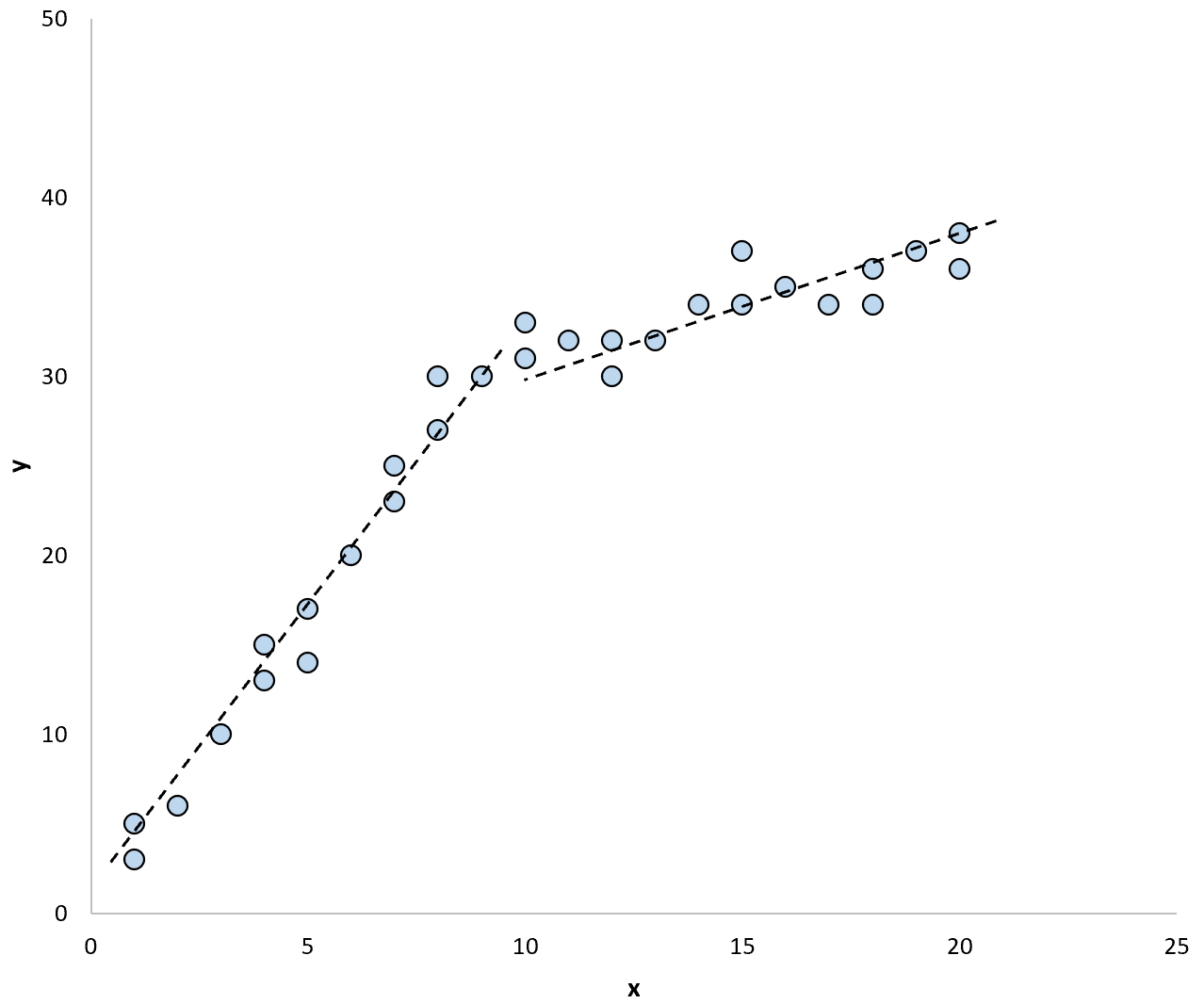
Chow 检验允许我们测试每条回归线的回归系数是否相等。

如果测试确定回归线之间的系数不相等，则意味着数据中有明显的结构断裂证据。也就是说，这个结构性断点前后的数据走势有很大不同。

何时使用 Chow 测试

以下示例说明了您可能想要执行 Chow 测试的情况：

1.确定选举前后股价走势是否不同。

2.确定利率变化前后房价是否变化。

3.确定新税法实施前后公营企业的平均利润是否存在差异。

在每种情况下，我们都可以使用 Chow 检验来确定在任何给定时间数据中是否存在结构断点。

执行 Chow 测试的步骤

我们可以使用以下步骤来执行 Chow 测试。

步骤 1：定义原假设和备择假设。

假设我们将以下回归模型拟合到整个数据集：

• y _t = a + bx _1t + cx _t2 + ε

接下来，假设我们根据结构断点将数据分为两组，并对每组拟合以下回归模型：

• y _t = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

我们将使用以下原假设和备择假设进行 Chow 检验：

• 空 (H ₀ )： a ₁ = a ₂ 、b ₁ = b ₂且 c ₁ = c ₂
• 替代方案 (H _A )： Null 中的至少一项比较不相等。

如果我们拒绝零假设，我们就有足够的证据表明数据中存在结构断点，并且两条回归线比一条回归线更能拟合数据。

如果我们未能拒绝零假设，我们就没有足够的证据表明数据中存在结构性断点。在这种情况下，我们说回归线可以“集中”为一条足以很好地表示数据模式的回归线。

步骤2：计算检验统计量。

如果我们定义以下术语：

• S _T ：总数据残差的平方和
• S ₁ , S ₂ : 每组残差的平方和
• N ₁ , N ₂ ：每组中的观察数
• k：参数个数

然后我们可以说 Chow 检验统计量为：

Chow 检验统计量 = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

该检验统计量遵循具有k和 N ₁ +N ₂ -2k 自由度的 F 分布。

步骤 3：拒绝或不拒绝原假设。

如果与此检验统计量相关的 p 值低于一定的显着性水平，我们可以拒绝零假设并得出数据中存在结构断点的结论。

幸运的是，大多数统计软件都能够执行 Chow 测试，因此您可能永远不需要手动执行测试。

执行 Chow 测试的示例

请参阅本教程，了解如何在 R 中对给定数据集执行 Chow 测试的分步示例。

周测试笔记

以下是有关 Chow 测试的一些注意事项：

1.检验假设回归模型的残差独立且同分布于方差未知的正态分布。

2.仅当您希望测试的结构断裂在已知时间发生时才应使用 Chow 测试。换句话说，不应重复使用该测试来确定给定时刻是否可以被视为结构断裂。