方差分析中高 f 值意味着什么?
单向方差分析用于确定三个或更多独立组的平均值是否相等。
单向方差分析使用以下原假设和备择假设:
- H 0 :所有组平均值相等。
- H A :至少一组平均值与其他组不同。
每次执行单向方差分析时,您最终都会得到一个如下所示的汇总表:
| 来源 | 平方和 (SS) | df | 均方 (MS) | F | P值 |
|---|---|---|---|---|---|
| 治疗 | 192.2 | 2 | 96.1 | 2,358 | 0.1138 |
| 错误 | 1100.6 | 27 | 40.8 | ||
| 全部的 | 1292.8 | 29 |
表中F值计算公式如下:
- F 值 = 均方处理 / 均方误差
另一种写法是:
- F 值 = 样本均值之间的变异 / 样本内的变异
如果样本均值之间的变异与每个样本内的变异相比较高,则 F 值将会很大。
例如上表中的F值计算如下:
- F 值 = 96.1 / 40.8 = 2.358
为了找到与该 F 值相对应的p 值,我们可以使用F 分布计算器,其中分子的自由度 = df 处理,分母的自由度 = df 误差。
例如,对应于 F 值 2.358、分子 df = 2、分母 df = 27 的 p 值为0.1138 。
由于该 p 值不小于 α = 0.05,因此我们无法拒绝原假设。这意味着三组的平均值之间不存在统计学上的显着差异。
查看方差分析的 F 值
为了直观地了解方差分析表中的 F 值,请考虑以下示例。
假设我们想要执行单向方差分析来确定三种不同的学习方法是否会产生不同的平均考试成绩。下表显示了使用每种技术的 10 名学生的考试结果:
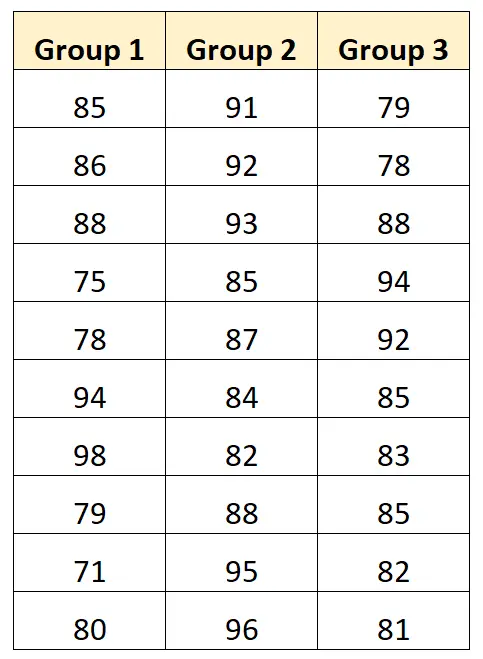
我们可以创建以下图表来按组可视化考试结果:
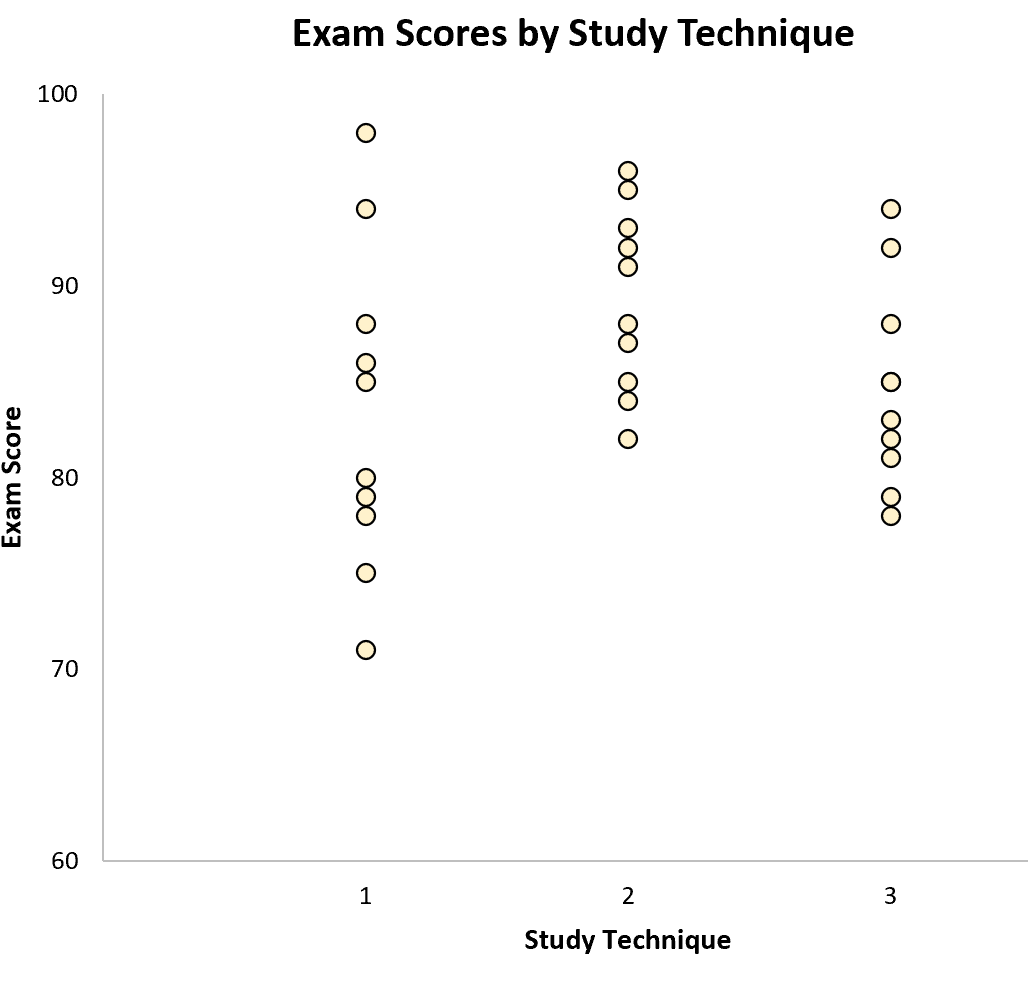
样本内的变异由每个样本内的值的分布表示:
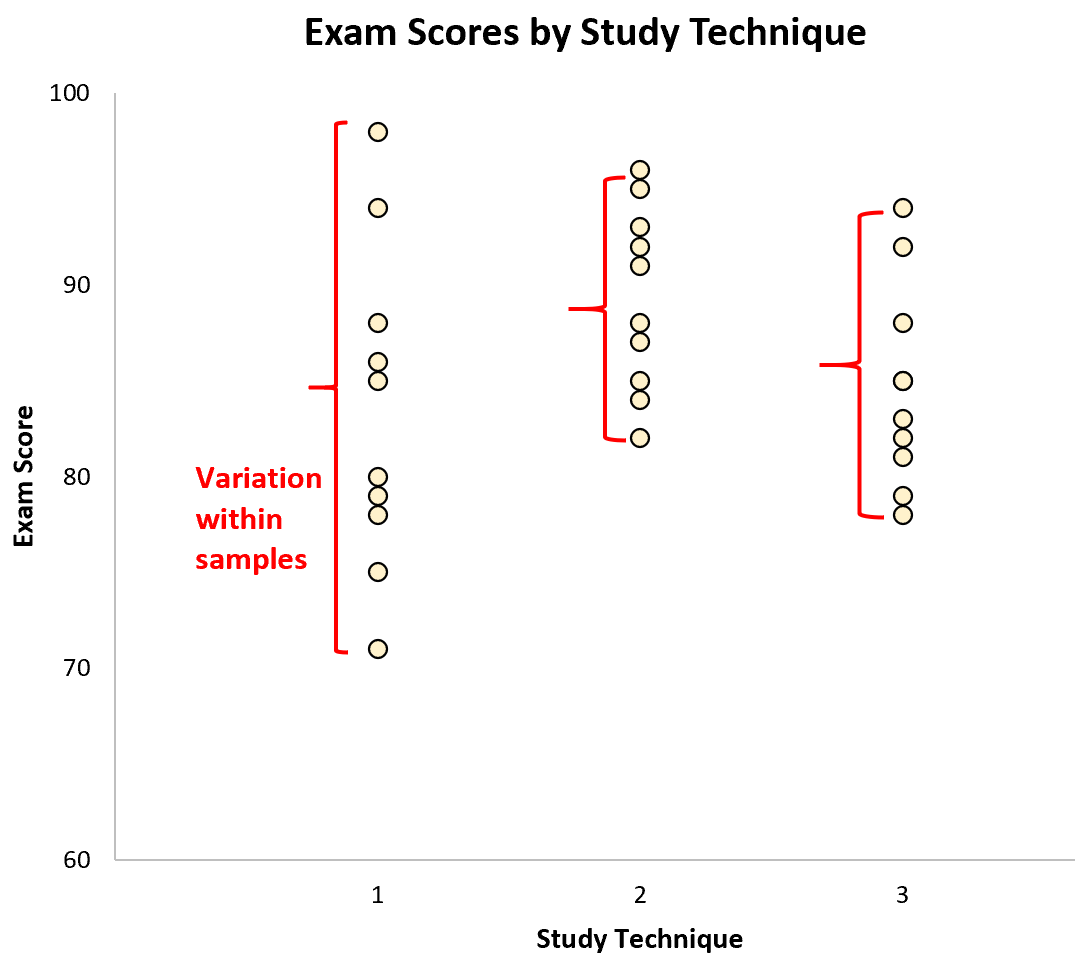
样本之间的变异由样本均值之间的差异表示:
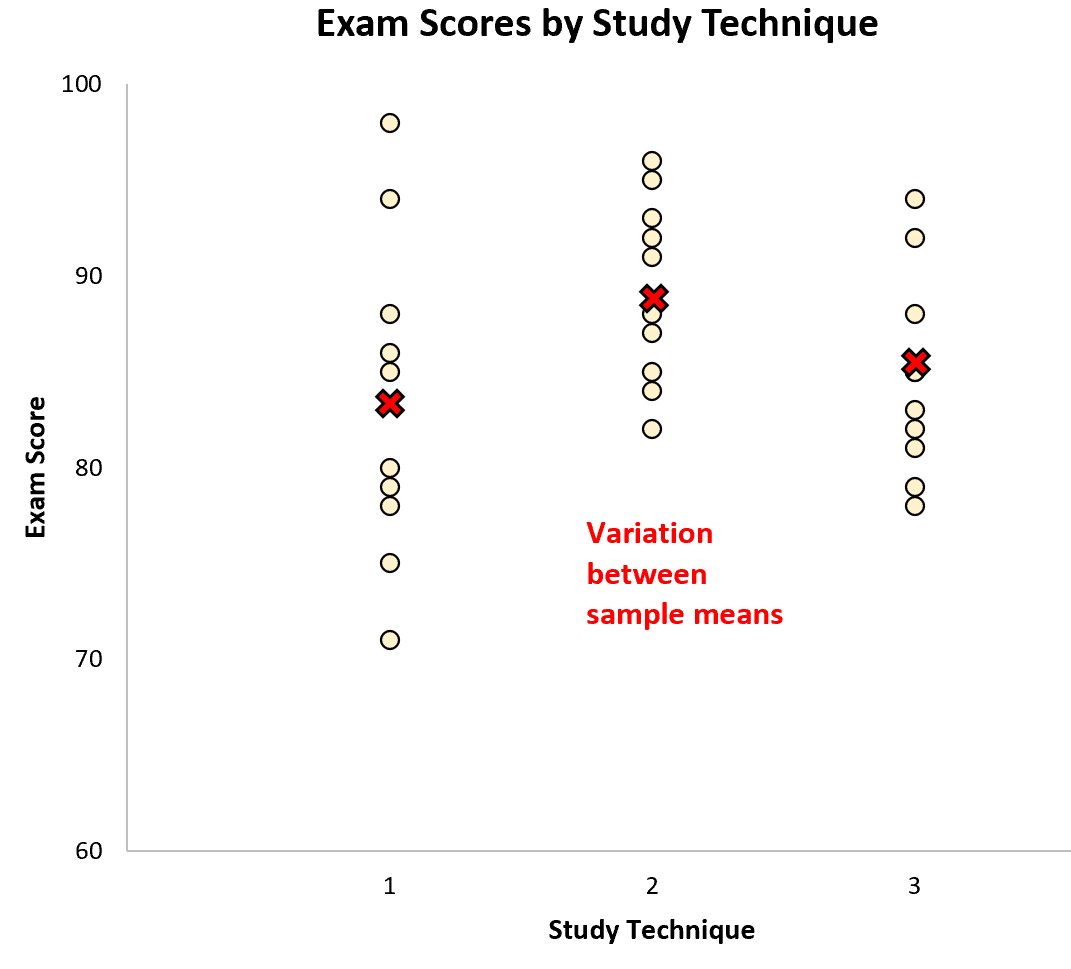
对此数据集执行单向方差分析,我们发现 F 值为2.358 ,相应的 p 值为0.1138 。
由于该 p 值不小于 0.05,因此我们无法拒绝原假设。这意味着我们没有足够的证据表明所使用的研究技术会导致平均考试成绩存在统计上的显着差异。
换句话说,这告诉我们样本均值之间的变异相对于样本内的变异来说不够高,不足以拒绝原假设。
结论
下面简单总结一下这篇文章的要点:
- 方差分析中的 F 值计算如下:样本均值之间的变异/样本内的变异。
- 方差分析中的 F 值越高,样本均值之间相对于样本内变化的变化就越大。
- F值越高,相应的p值越低。
- 如果 p 值低于某个阈值(例如 α = 0.05),我们可以拒绝方差分析的原假设,并得出结论:组均值之间存在统计显着差异。