泊松分布或正态分布：有什么区别？

泊松分布和正态分布是统计学中最常用的两种概率分布。

本教程提供了每个发行版的快速说明以及发行版之间的两个主要区别。

概述：泊松分布

泊松分布描述了在给定时间间隔内获得k 次成功的概率。

如果随机变量X服从泊松分布，则X = k成功的概率可以通过以下公式求出：

P(X=k) = λ ^k * e ^{– λ} / k!

金子：

• λ：特定时间间隔内发生的平均成功次数
• k：成功次数
• e：约等于 2.71828 的常数

例如，假设某家医院平均每小时分娩 2 名婴儿。我们可以使用上面的公式来确定给定小时内经历 3 次出生的概率：

P(X=3) = 2 ³ * e ^{– 2} / 3！ = 0.1805

在给定的一小时内经历 3 次分娩的概率是0.1805 。

概述：正态分布

正态分布描述了随机变量在给定区间内取值的概率。

正态分布的概率密度函数可以写为：

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

金子：

• σ：分布的标准偏差
• μ：分布的平均值
• x：随机变量的值

例如，假设某种水獭的重量服从正态分布，μ = 40 磅，σ = 5 磅。

如果我们从这个种群中随机选择一只水獭，我们可以使用以下公式来计算它的体重在 38 到 42 磅之间的概率：

P ( ^{38 < /5) 2} = 0.3108

随机选择的水獭体重在 38 到 42 磅之间的概率是0.3108 。

区别#1：谨慎与谨慎连续数据

泊松分布和正态分布之间的第一个区别是每个概率分布建模的数据类型。

当处理只能取等于或大于零的整数值的离散数据时，使用泊松分布。这里有些例子：

• 呼叫中心每小时接听的电话数量
• 餐厅每天的顾客数量
• 每月车祸数量

在每种情况下，随机变量只能取值0、1、2、3等。

当处理可以取从负无穷大到正无穷大的任何值的连续数据时，使用正态分布。这里有些例子：

• 某种动物的体重
• 某种植物的高度
• 女子马拉松时间
• 温度（摄氏度）

在这些场景中，随机变量可以采用任何值，例如 -11.3、21.343435、85 等。

差异#2：分布形状

泊松分布与正态分布的第二个区别在于分布的形状。

正态分布总是呈钟形：

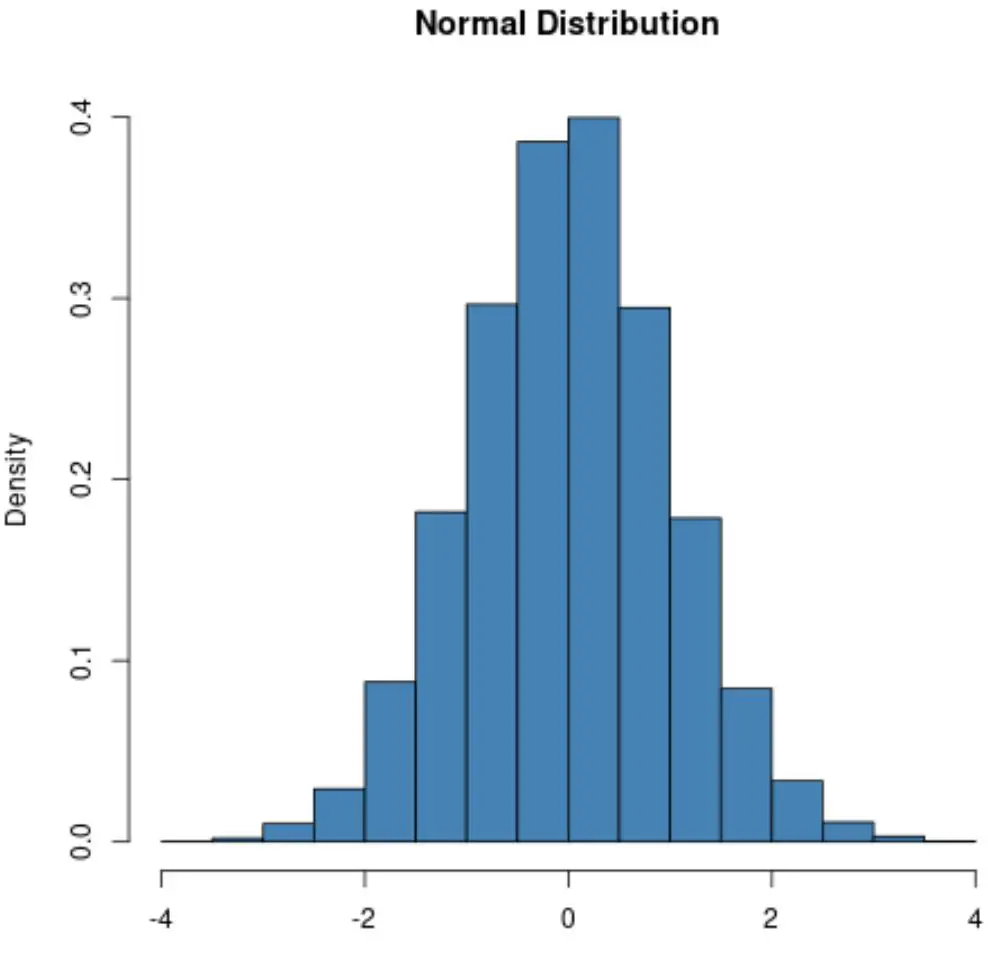
然而，泊松分布的形状根据分布的平均值而变化。

例如，均值较小（如μ = 3）的泊松分布将严重右偏：

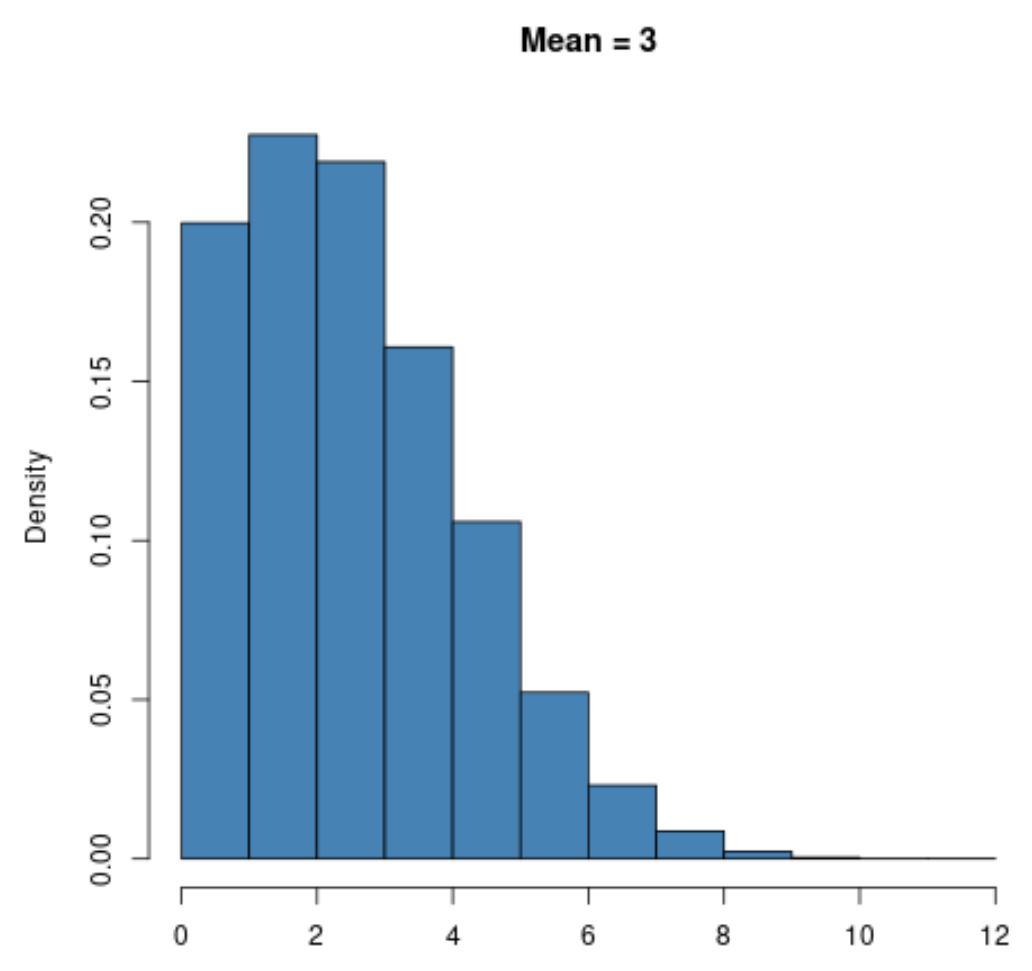
然而，具有较大平均值（如μ = 20）的泊松分布将呈现出钟形，就像正态分布一样：

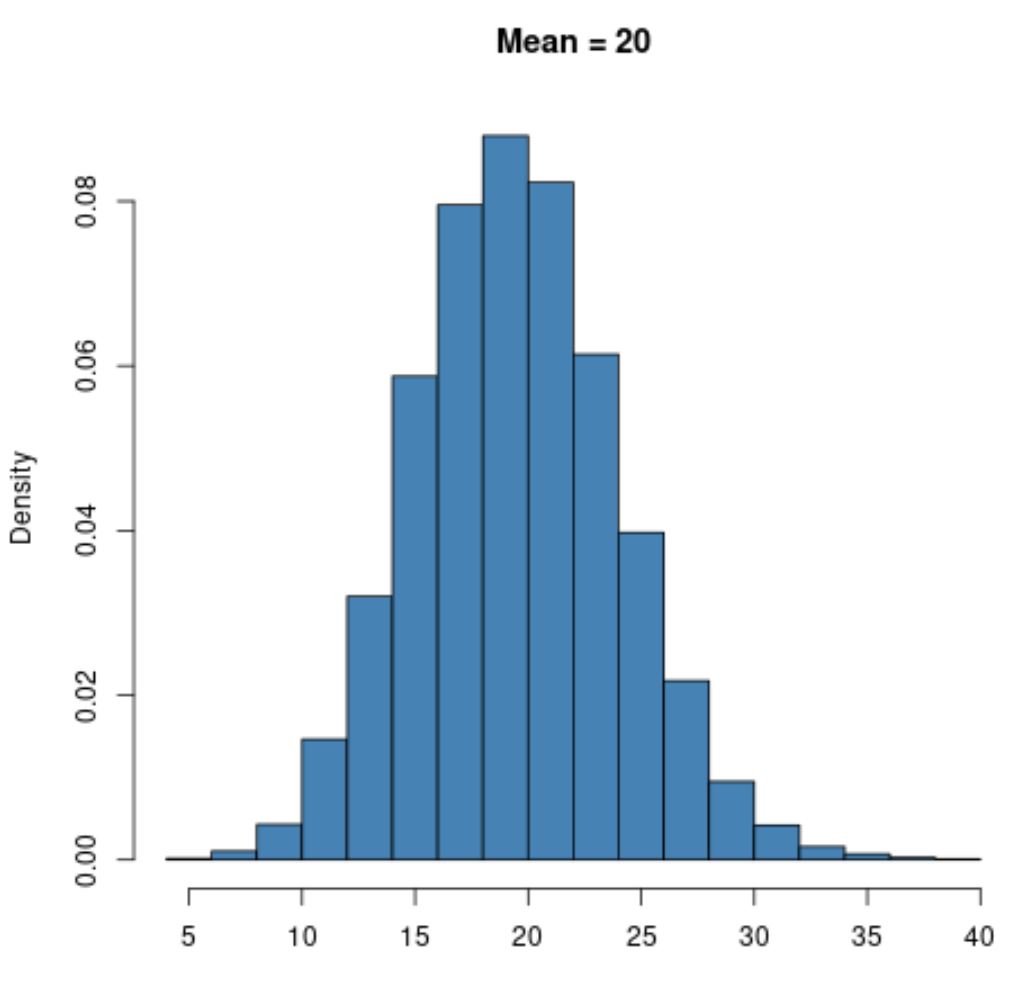
请注意，无论平均值是多少，泊松分布的下界始终为零，因为泊松分布只能用于等于或大于零的整数值。

其他资源

以下教程提供有关泊松分布的更多信息：

泊松分布简介
泊松分布的四个假设
泊松分布的 5 个具体例子

以下教程提供有关正态分布的其他信息：

正态分布简介
正态分布的 6 个具体例子
正态分布数据集生成器