泊松分布简介
泊松分布是统计学中最流行的分布之一。
要理解泊松分布,首先了解泊松实验会很有帮助。
鱼类实验
泊松实验是具有以下性质的实验:
- 实验成功的次数是可以统计的。
- 在特定时间(或空间)间隔内发生的平均成功次数是已知的。
- 每个结果都是独立的。
- 成功发生的概率与间隔的大小成正比。
泊松实验的一个例子是给定医院每小时的出生人数。例如,假设某家医院平均每小时分娩 10 名婴儿。这是泊松实验,因为它具有以下四个性质:
- 实验成功的次数是可以计算的——我们可以计算出生的数量。
- 特定时间间隔内发生的平均出生人数是已知的 – 已知每小时平均有 10 名新生儿出生。
- 每个结果都是独立的——一位母亲在给定时间内分娩的概率与另一位母亲分娩的概率无关。
- 成功发生的概率与间隔的大小成正比:时间间隔越长,发生的概率就越高。
我们可以使用泊松分布来回答有关泊松实验的概率问题,例如:
- 给定时间内发生 12 次以上分娩的概率是多少?
- 给定小时内出生人数少于 5 人的概率是多少?
- 给定小时内发生 8 到 11 次分娩的概率是多少?
鱼类分布
泊松分布描述了在给定时间间隔内获得k 次成功的概率。
如果随机变量X服从泊松分布,则X = k成功的概率可以通过以下公式求得:
P(X=k) = λ k * e – λ / k!
金子:
- λ:特定时间间隔内发生的平均成功次数
- k:成功次数
- e:约等于 2.71828 的常数
例如,假设某家医院平均每小时分娩 2 名婴儿。我们可以使用上面的公式来确定经历0、1、2、3次出生等的概率。在给定的时间内:
P(X=0) = 2 0 * e – 2 / 0! = 0.1353
P(X=1) = 2 1 * e – 2 / 1! = 0.2707
P(X=2) = 2 2 * e – 2 / 2! = 0.2707
P(X=3) = 2 3 * e – 2 / 3! = 0.1805
我们可以计算任意数量的出生的概率,直到无穷大。然后我们创建一个简单的直方图来可视化该概率分布:

累积泊松概率的计算
使用上面的公式计算单个泊松概率(例如,一家医院在给定时间内发生 3 次分娩的概率)很简单,但要计算累积泊松概率,我们需要添加各个概率。
例如,假设我们想知道医院在给定小时内分娩 1 例或更少的概率。我们将使用以下公式来计算该概率:
P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406
这称为累积概率,因为它涉及添加多个概率。我们可以使用类似的公式计算在给定小时内经历k或更少出生的累积概率:
P(X≤0) = P(X=0) = 0.1353
P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406
P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0.1353 + 0.2707 + 0.2707 = 0.6767
我们可以计算任意数量的出生的累积概率,直到无穷大。然后我们可以创建一个直方图来可视化这个累积概率分布:
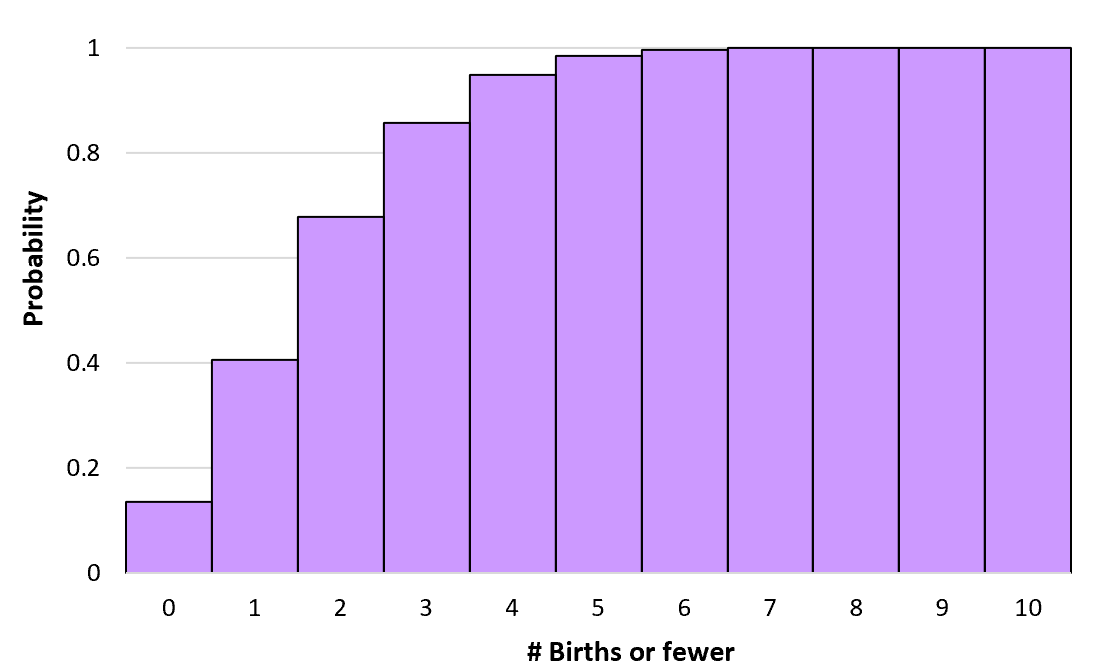
泊松分布的性质
泊松分布具有以下性质:
分布的平均值是λ 。
分布的方差也是λ 。
分布的标准差为√ λ 。
例如,假设一家医院平均每小时分娩 2 名婴儿。
给定小时内的平均预期出生人数为 λ = 2 次出生。
我们期望的出生数量的方差是 λ = 2 出生。
鱼类配送实践问题
使用以下练习题来测试您对泊松分布的了解。
注意:我们将使用泊松分布计算器来计算这些问题的答案。
问题1
问题:我们知道某个网站每小时销售额为 10 笔。在给定的小时内,该网站恰好实现 8 笔销售的概率是多少?
答案:使用泊松分布计算器,其中 λ = 10 且 x = 8,我们发现 P(X=8) = 0.1126 。
问题2
问题:我们知道某房地产经纪人平均每月销售额为 5 笔。在给定的一个月内,她的销售额超过 7 笔的概率是多少?
答案:使用泊松分布计算器,其中 λ = 5 且 x = 7,我们发现 P(X>7) = 0.13337 。
问题3
问:我们知道某医院每小时分娩4次。在给定的小时内,出生人数为 4 人或更少的概率是多少?
答案:使用泊松分布计算器,其中 λ = 4 且 x = 4,我们发现 P(X≤4) = 0.62884 。
其他资源
以下文章解释了如何在不同的统计软件中使用泊松分布:
如何在 R 中使用泊松分布
如何在Excel中使用泊松分布
如何在 TI-84 计算器上计算泊松概率
泊松分布的现实示例
鱼类分布计算器