如何在 ti-84 计算器上计算泊松概率

泊松分布是所有统计中最常用的分布之一。本教程介绍如何在 TI-84 计算器上使用以下函数来计算泊松概率：

Poissonpdf(mean, x)返回与 Poisson pdf 相关的概率。

Poissoncdf(mean, x)返回与泊松 cdf 相关的累积概率。

金子：

• 平均值= 平均“成功”次数
• x = “成功”的具体数量

在 TI-84 计算器上，可以通过按2nd然后按vars来访问这两个函数。这将带您进入DISTR屏幕，您可以在其中使用fishpdf()和fishcdf() ：

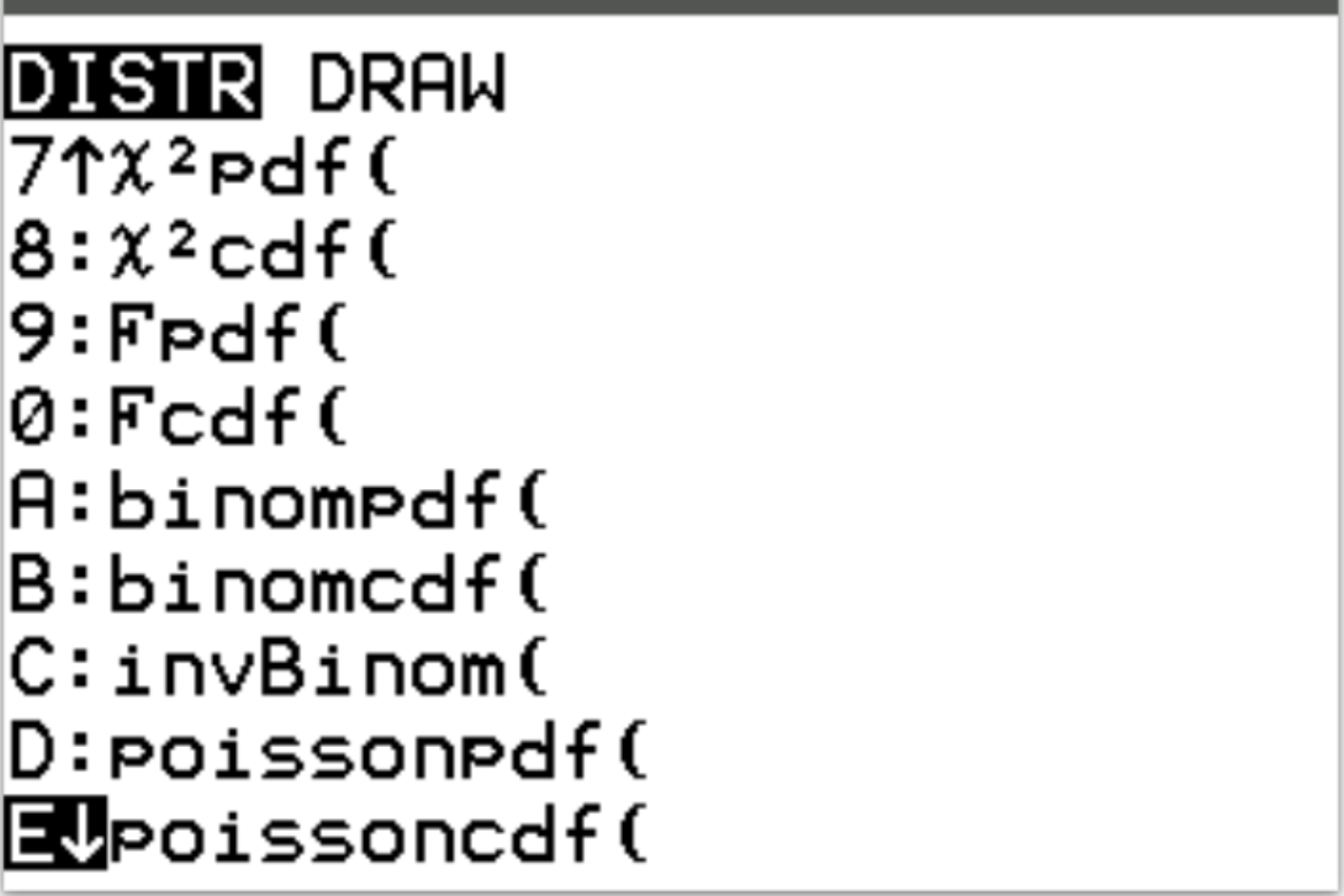
以下示例说明了如何使用这些函数来回答不同的问题。

示例 1：恰好 x 成功的泊松概率

问题：一家五金店平均每天销售 3 个锤子。他们在某一天卖出 5 个锤子的概率是多少？

答案：使用 Poissonpdf(mean, x) 函数：

鱼pdf(3, 5) = 0.1008

示例 2：小于 x 成功的泊松概率

问题：一家五金店平均每天销售 3 个锤子。他们在某一天卖出少于 5 个锤子的概率是多少？

答案：使用 Poissoncdf(mean, x-1) 函数：

鱼cdf(3, 4) = 0.8153

示例 3：最多 x 成功的泊松概率

问题：一家五金店平均每天销售 3 个锤子。他们在某一天最多卖出 5 个锤子的概率是多少？

答案：使用 Poissoncdf(mean, x) 函数：

鱼cdf(3, 5) = 0.9161

示例 4：超过 x 成功的泊松概率

问题：一家五金店平均每天销售 3 个锤子。他们在某一天卖出超过 5 个锤子的概率是多少？

答案：使用函数 1 – Poissoncdf(mean, x)：

1 – 鱼cdf(3, 5) = 0.0839

示例 5：至少 x 成功的泊松概率

问题：一家五金店平均每天销售 3 个锤子。他们在某一天至少卖出 5 把锤子的概率是多少？

答案：使用函数 1 – Poissoncdf(mean, x-1)：

1 – 鱼cdf(3, 4) = 0.1847