Eine vollständige anleitung: der 2×2-faktorielle versuchsplan

Ein 2 × 2-faktorielles Design ist eine Art experimentelles Design, das es Forschern ermöglicht, die Auswirkungen zweier unabhängiger Variablen (jeweils mit zwei Ebenen ) auf eine einzelne abhängige Variable zu verstehen.

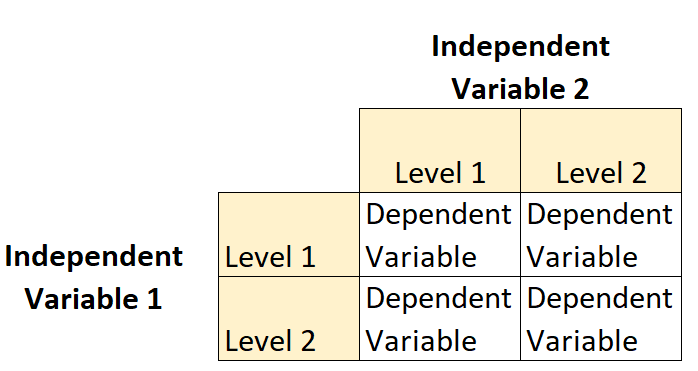
Angenommen, ein Botaniker möchte die Auswirkungen von Sonnenlicht (niedrig oder hoch) und der Bewässerungshäufigkeit (täglich oder wöchentlich) auf das Wachstum einer bestimmten Pflanzenart verstehen.

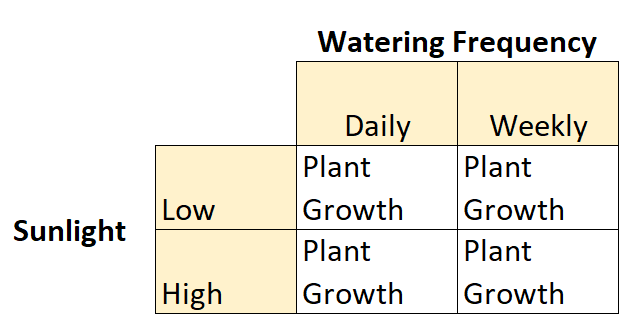
Dies ist ein Beispiel für einen 2×2-faktoriellen Entwurf, da es zwei unabhängige Variablen mit jeweils zwei Ebenen gibt:

• Unabhängige Variable Nr. 1: Sonnenlicht
  • Stufen: niedrig, hoch
• Unabhängige Variable Nr. 2: Bewässerungshäufigkeit
  • Levels: täglich, wöchentlich

Und es gibt eine abhängige Variable: das Pflanzenwachstum.

Der Zweck eines 2 × 2-faktoriellen Designs

Ein 2×2-faktorielles Design ermöglicht die Analyse folgender Effekte:

Haupteffekte: Dies sind die Auswirkungen, die eine einzelne unabhängige Variable auf die abhängige Variable hat.

In unserem vorherigen Szenario könnten wir beispielsweise die folgenden Haupteffekte analysieren:

• Hauptwirkung des Sonnenlichts auf das Pflanzenwachstum.
  • Wir können das durchschnittliche Wachstum aller Pflanzen ermitteln, die wenig Sonnenlicht erhalten haben.
  • Wir können das durchschnittliche Wachstum aller Pflanzen ermitteln, die viel Sonnenlicht erhalten haben.
• Hauptwirkung der Bewässerungshäufigkeit auf das Pflanzenwachstum.
  • Wir können das durchschnittliche Wachstum aller täglich gegossenen Pflanzen ermitteln.
  • Wir können das durchschnittliche Wachstum aller Pflanzen ermitteln, die jede Woche bewässert werden.

Interaktionseffekte: Sie treten auf, wenn die Wirkung einer unabhängigen Variablen auf die abhängige Variable vom Niveau der anderen unabhängigen Variablen abhängt.

In unserem vorherigen Szenario könnten wir beispielsweise die folgenden Interaktionseffekte analysieren:

• Hängt die Wirkung des Sonnenlichts auf das Pflanzenwachstum von der Bewässerungshäufigkeit ab?
• Hängt die Auswirkung der Bewässerungshäufigkeit auf das Pflanzenwachstum vom Sonnenlicht ab?

Visualisieren Sie Haupteffekte und Interaktionseffekte

Wenn wir einen 2 × 2-faktoriellen Entwurf verwenden, stellen wir häufig die Mittelwerte grafisch dar, um die Auswirkungen der unabhängigen Variablen auf die abhängige Variable besser zu verstehen.

Betrachten Sie beispielsweise die folgende Darstellung:

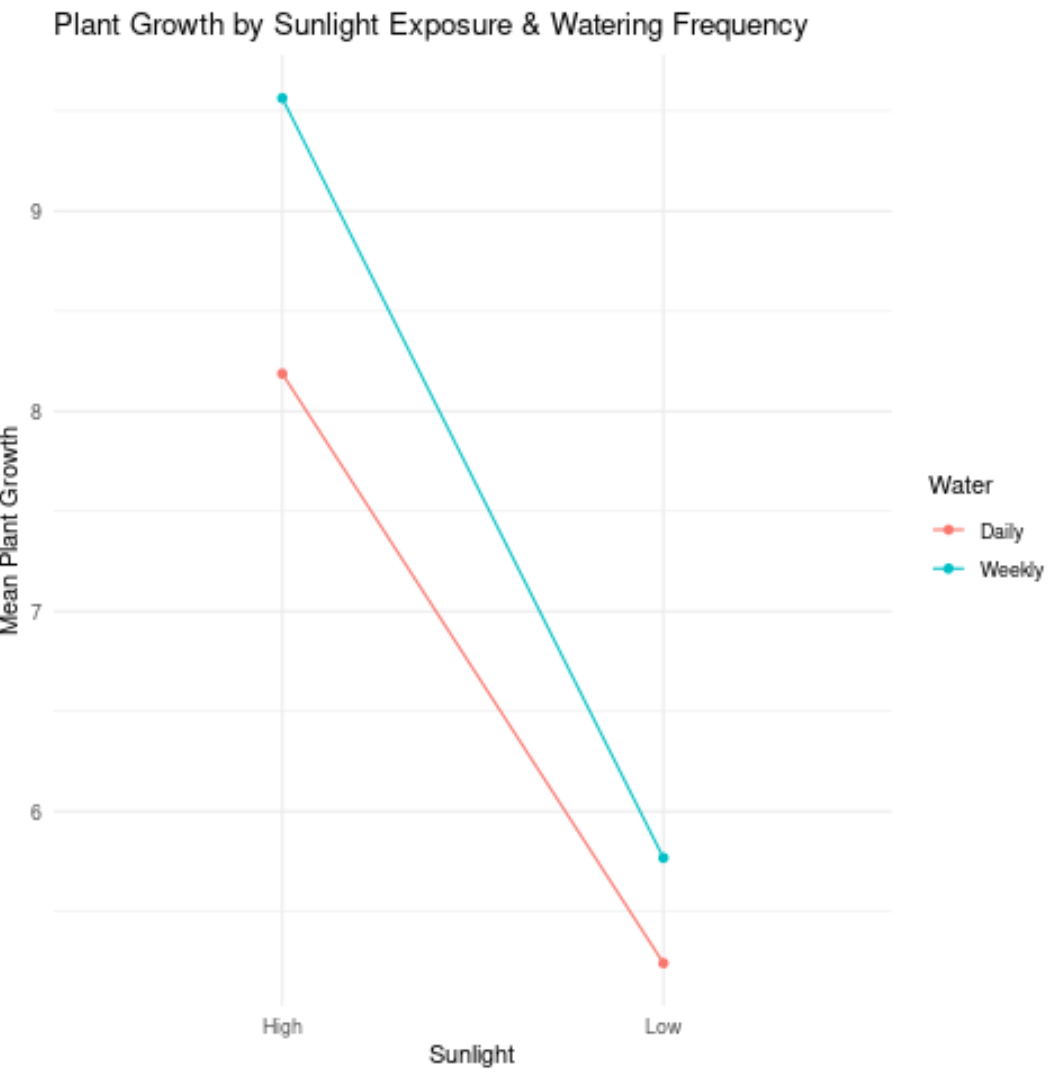
So interpretieren Sie die Werte im Diagramm:

• Das durchschnittliche Wachstum von Pflanzen, die intensivem Sonnenlicht und täglicher Bewässerung ausgesetzt waren, betrug etwa 20,5 Zentimeter.
• Das durchschnittliche Wachstum von Pflanzen, die viel Sonnenlicht und wöchentliche Bewässerung erhielten, betrug etwa 9,6 Zoll.
• Das durchschnittliche Wachstum der Pflanzen, die wenig Sonne erhielten und täglich gegossen wurden, betrug etwa 5,3 Zoll.
• Das durchschnittliche Wachstum der Pflanzen, die wenig Sonne erhielten und wöchentlich gegossen wurden, betrug etwa 5,8 Zoll.

Um festzustellen, ob es einen Interaktionseffekt zwischen den beiden unabhängigen Variablen gibt, prüfen Sie einfach, ob die Linien parallel sind oder nicht:

• Wenn die beiden Linien des Diagramms parallel sind, gibt es keinen Interaktionseffekt.
• Wenn die beiden Linien des Diagramms nicht parallel sind, liegt ein Interaktionseffekt vor.

In der vorherigen Grafik verliefen die beiden Linien ungefähr parallel, sodass es wahrscheinlich keinen Wechselwirkungseffekt zwischen der Bewässerungshäufigkeit und der Sonneneinstrahlung gibt.

Betrachten Sie jedoch die folgende Handlung:

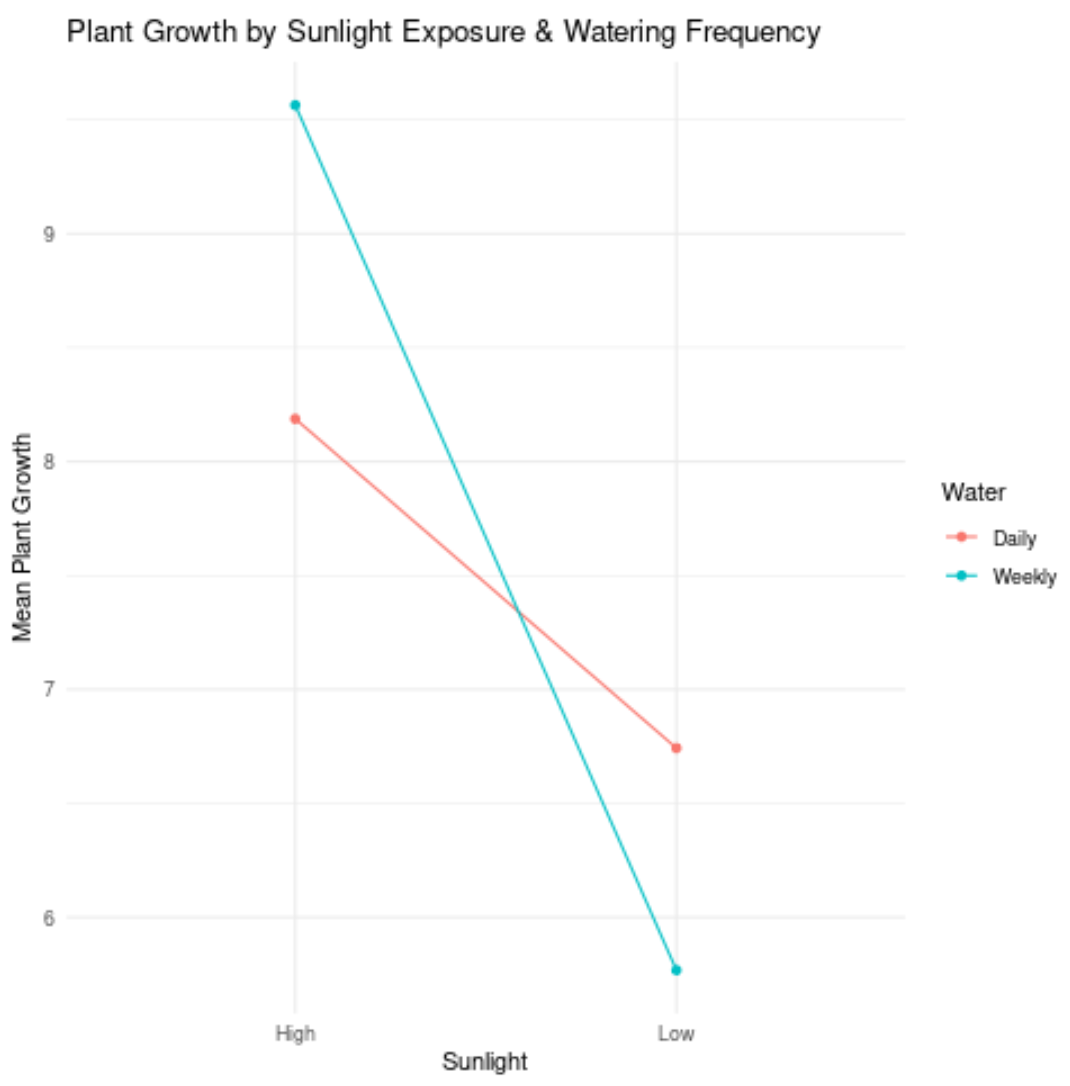
Die beiden Linien sind überhaupt nicht parallel (tatsächlich schneiden sie sich!), was darauf hindeutet, dass wahrscheinlich ein Wechselwirkungseffekt zwischen ihnen besteht.

Das bedeutet zum Beispiel, dass die Wirkung des Sonnenlichts auf das Pflanzenwachstum von der Häufigkeit des Gießens abhängt .

Mit anderen Worten: Sonnenlicht und Bewässerungshäufigkeit haben keinen unabhängigen Einfluss auf das Pflanzenwachstum. Vielmehr besteht ein Interaktionseffekt zwischen den beiden unabhängigen Variablen.

So analysieren Sie einen 2×2-faktoriellen Versuchsplan

Das Zeichnen von Durchschnittswerten ist eine visuelle Möglichkeit, die Auswirkungen unabhängiger Variablen auf die abhängige Variable zu untersuchen.

Wir können jedoch auch eine zweifaktorielle ANOVA durchführen, um formal zu testen, ob die unabhängigen Variablen eine statistisch signifikante Beziehung zur abhängigen Variablen haben oder nicht.

Der folgende Code zeigt beispielsweise, wie eine zweifaktorielle ANOVA für unser hypothetisches Fabrikszenario in R durchgeführt wird:

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

So interpretieren Sie das ANOVA-Ergebnis:

• Der mit Sonnenlicht verbundene p-Wert beträgt 0,005 . Da dieser Wert unter 0,05 liegt, bedeutet dies, dass die Sonneneinstrahlung einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat.
• Der mit Wasser verbundene p-Wert beträgt 0,028 . Da dieser Wert unter 0,05 liegt, bedeutet dies, dass die Bewässerungshäufigkeit auch einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat.
• Der p-Wert für die Wechselwirkung zwischen Sonnenlicht und Wasser beträgt 0,156 . Da dieser Wert nicht weniger als 0,05 beträgt, bedeutet dies, dass es keinen Wechselwirkungseffekt zwischen Sonnenlicht und Wasser gibt.

Zusätzliche Ressourcen

Eine vollständige Anleitung: der 2 × 3-faktorielle Versuchsplan
Was sind Stufen einer unabhängigen Variablen?
Unabhängige oder abhängige Variablen
Was ist eine faktorielle ANOVA?