Eine vollständige anleitung: der 2×4-faktorielle versuchsplan

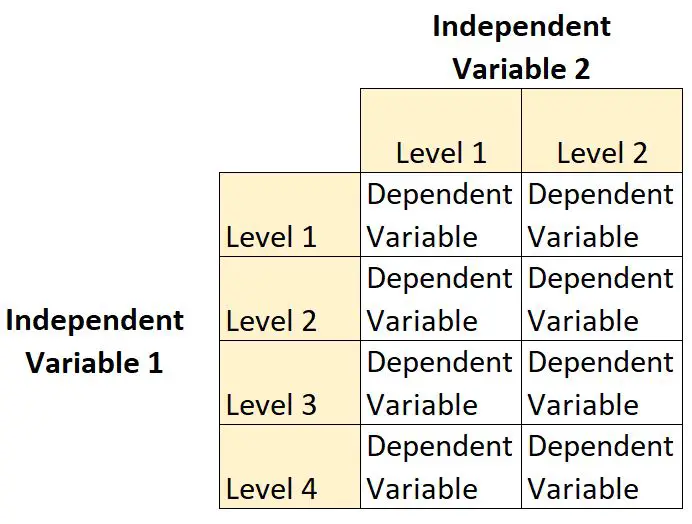
Ein 2 × 4-faktorielles Design ist eine Art experimentelles Design, das es Forschern ermöglicht, die Auswirkungen zweier unabhängiger Variablen auf eine einzelne abhängige Variable zu verstehen.

Bei diesem Designtyp hat eine unabhängige Variable zwei Ebenen und die andere unabhängige Variable vier Ebenen.

Angenommen, ein Botaniker möchte die Auswirkungen von Sonnenlicht (kein, niedrig, mittel oder hoch) und der Bewässerungshäufigkeit (täglich oder wöchentlich) auf das Wachstum einer bestimmten Pflanzenart verstehen.

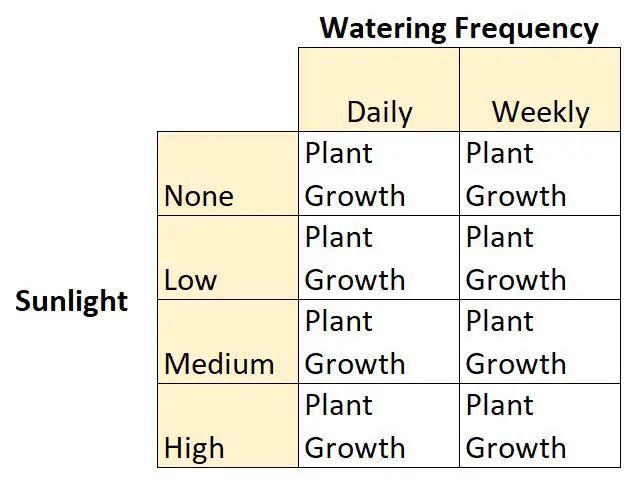
Dies ist ein Beispiel für einen 2 × 4-faktoriellen Entwurf, da es zwei unabhängige Variablen gibt, eine mit zwei Ebenen und eine mit vier Ebenen:

• Unabhängige Variable Nr. 1: Sonnenlicht
  • Stufen: Keine, Niedrig, Mittel, Hoch
• Unabhängige Variable Nr. 2: Bewässerungshäufigkeit
  • Levels: täglich, wöchentlich

Und es gibt eine abhängige Variable: das Pflanzenwachstum.

Der Zweck eines 2 × 4-faktoriellen Designs

Ein 2×4-faktorielles Design ermöglicht die Analyse folgender Effekte:

Haupteffekte: Dies sind die Auswirkungen, die eine einzelne unabhängige Variable auf die abhängige Variable hat.

In unserem vorherigen Szenario könnten wir beispielsweise die folgenden Haupteffekte analysieren:

• Hauptwirkung des Sonnenlichts auf das Pflanzenwachstum.
  • Durchschnittliches Wachstum aller Pflanzen, die kein Sonnenlicht erhielten.
  • Durchschnittliches Wachstum aller Pflanzen, die wenig Sonnenlicht erhielten.
  • Durchschnittliches Wachstum aller Pflanzen, die durchschnittlich Sonnenlicht erhalten haben.
  • Durchschnittliches Wachstum aller Pflanzen, die viel Sonnenlicht erhielten.
• Hauptwirkung der Bewässerungshäufigkeit auf das Pflanzenwachstum.
  • Durchschnittliches Wachstum aller täglich bewässerten Pflanzen.
  • Durchschnittliches Wachstum aller wöchentlich bewässerten Pflanzen.

Interaktionseffekte: Sie treten auf, wenn die Wirkung einer unabhängigen Variablen auf die abhängige Variable vom Niveau der anderen unabhängigen Variablen abhängt.

In unserem vorherigen Szenario könnten wir beispielsweise die folgenden Interaktionseffekte analysieren:

• Hängt die Wirkung des Sonnenlichts auf das Pflanzenwachstum von der Bewässerungshäufigkeit ab?
• Hängt die Auswirkung der Bewässerungshäufigkeit auf das Pflanzenwachstum vom Sonnenlicht ab?

So analysieren Sie einen 2 × 4-faktoriellen Versuchsplan

Wir können eine zweifaktorielle ANOVA durchführen, um formal zu testen, ob die unabhängigen Variablen eine statistisch signifikante Beziehung zur abhängigen Variablen haben oder nicht.

Der folgende Code zeigt beispielsweise, wie eine zweifaktorielle ANOVA für unser hypothetisches Fabrikszenario in R durchgeführt wird:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

So interpretieren Sie das ANOVA-Ergebnis:

Haupteffekt Nr. 1 (Sonnenlicht) : Der mit Sonnenlicht verbundene p-Wert beträgt <2e-16 . Da dieser Wert unter 0,05 liegt, bedeutet dies, dass die Sonneneinstrahlung einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat.

Haupteffekt Nr. 2 (Wasser) : Der mit Wasser verbundene p-Wert beträgt 0,016 . Da dieser Wert unter 0,05 liegt, bedeutet dies, dass die Bewässerungshäufigkeit auch einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat.

Wechselwirkungseffekt : Der p-Wert für die Wechselwirkung zwischen Sonnenlicht und Wasser beträgt 0,000061 . Da dieser Wert unter 0,05 liegt, bedeutet dies, dass es einen Wechselwirkungseffekt zwischen Sonnenlicht und Wasser gibt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zum experimentellen Design und zur Analyse:

Eine vollständige Anleitung: der 2 × 2-faktorielle Versuchsplan
Eine vollständige Anleitung: der 2 × 3-faktorielle Versuchsplan
Was ist eine faktorielle ANOVA?