So führen sie t-tests in google sheets durch

Im Allgemeinen gibt es drei Arten von t-Tests:

• Ein Beispiel-T-Test
• T-Test bei zwei Stichproben
• T-Test für gepaarte Stichproben

Dieses Tutorial enthält Beispiele für die Durchführung jedes dieser Tests in Google Sheets.

Beispiel: ein t-Test bei einer Stichprobe

Definition: Ein t-Test bei einer Stichprobe wird verwendet, um zu testen, ob der Mittelwert einer Grundgesamtheit einem bestimmten Wert entspricht oder nicht.

Beispiel: Ein Botaniker möchte wissen, ob die durchschnittliche Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Sie entnimmt eine Zufallsstichprobe von 12 Pflanzen und notiert deren Höhe in Zoll.

Der folgende Screenshot zeigt, wie Sie einen T-Test bei einer Stichprobe durchführen, um zu bestimmen, ob die tatsächliche mittlere Bevölkerungsgröße 15 Zoll beträgt:

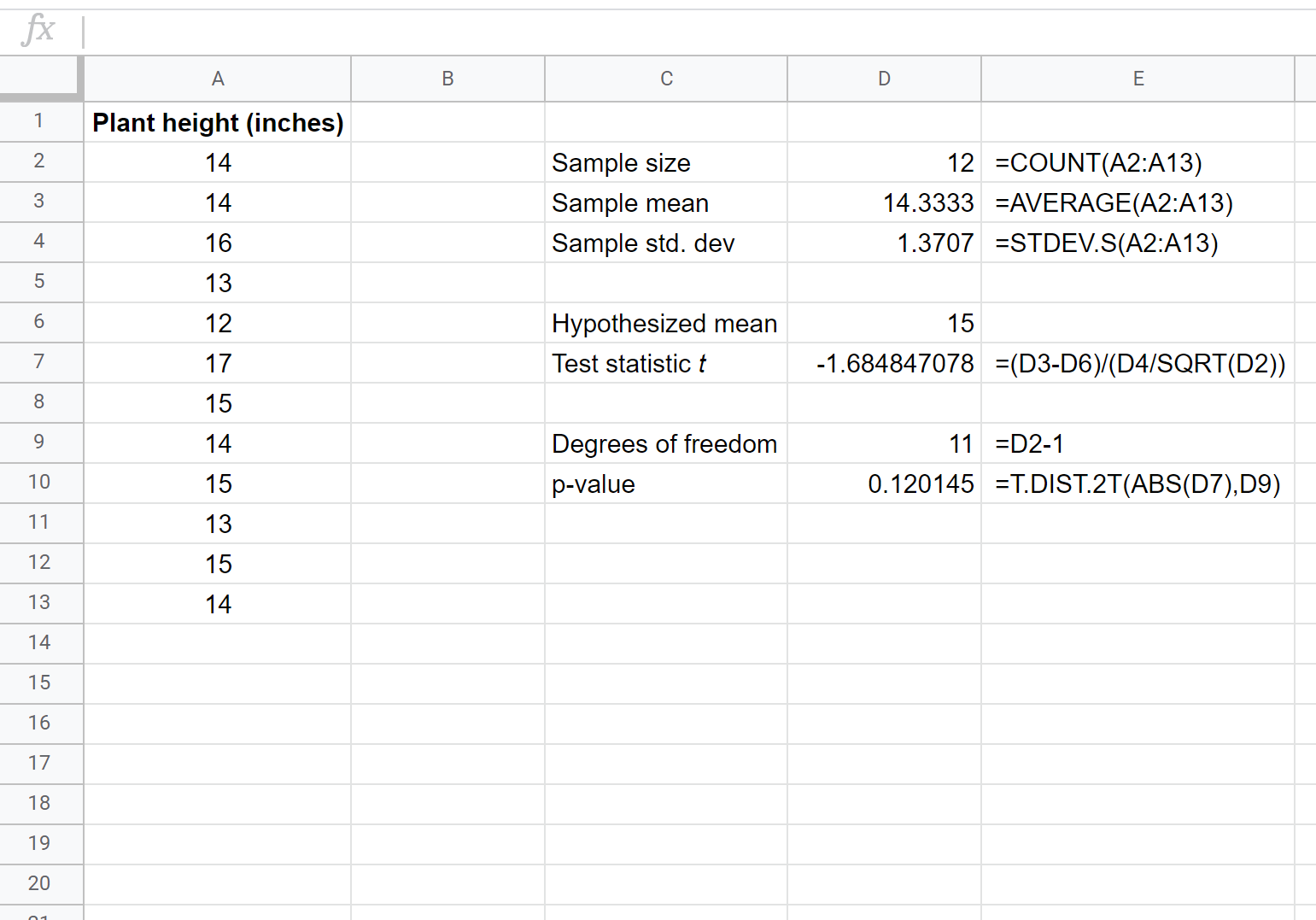
Die beiden Hypothesen für diesen t-Test für eine bestimmte Stichprobe lauten wie folgt:

H ₀ : µ = 15 (die durchschnittliche Höhe dieser Pflanzenart beträgt 15 Zoll)

H _A : µ ≠15 (durchschnittliche Höhe beträgt nicht 15 Zoll)

Da der p-Wert unseres Tests (0,120145) größer als Alpha = 0,05 ist, können wir die Nullhypothese des Tests nicht ablehnen. Wir haben keine ausreichenden Beweise dafür, dass die durchschnittliche Höhe dieser bestimmten Pflanzenart etwas anderes als 15 Zoll beträgt.

Beispiel: T-Test bei zwei Stichproben

Definition: Ein t-Test bei zwei Stichproben wird verwendet, um zu testen, ob die Mittelwerte zweier Grundgesamtheiten gleich sind oder nicht.

Beispiel: Forscher möchten wissen, ob zwei verschiedene Pflanzenarten in einem bestimmten Land die gleiche durchschnittliche Höhe haben. Sie sammeln eine Zufallsstichprobe von 20 Pflanzen jeder Art und zeichnen die Höhe jeder Pflanze in Zoll auf.

Der folgende Screenshot zeigt, wie Sie mit der Funktion T.TEST() einen T-Test bei zwei Stichproben durchführen, um zu bestimmen, ob die durchschnittlichen Höhen der beiden Grundgesamtheiten gleich sind:

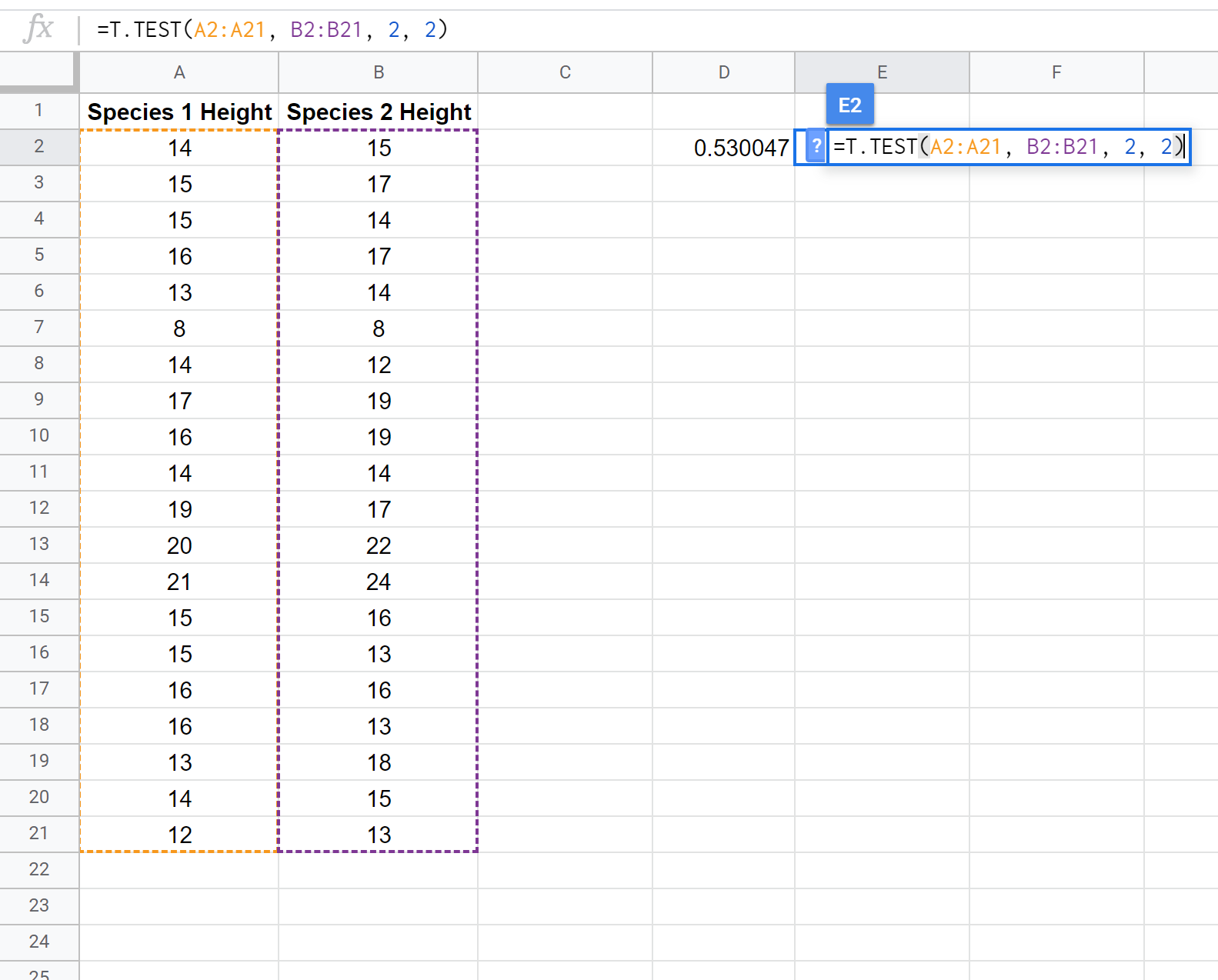
Hinweis: Es ist auch möglich, einen einseitigen t-Test bei zwei Stichproben mit oder ohne der Annahme durchzuführen, dass die beiden Stichproben die gleiche Varianz aufweisen. Informationen zum Anpassen der Testannahmen finden Sie in der T.TEST-Dokumentation .

Die beiden Hypothesen für diesen T-Test bei zwei Stichproben lauten:

H ₀ : μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)

H ₁ : μ ₁ ≠ μ ₂ (die beiden Populationsmittelwerte sind nicht gleich)

Da der p-Wert unseres Tests (0,530047) größer als Alpha = 0,05 ist, können wir die Nullhypothese des Tests nicht ablehnen. Wir haben keine ausreichenden Beweise dafür, dass die durchschnittliche Höhe dieser bestimmten Pflanzenart etwas anderes als 15 Zoll beträgt.

Beispiel: T-Test für gepaarte Stichproben

Definition: Ein t-Test für gepaarte Stichproben wird verwendet, um die Mittelwerte zweier Stichproben zu vergleichen, wenn jede Beobachtung aus einer Stichprobe mit einer Beobachtung aus der anderen Stichprobe verknüpft werden kann.

Beispiel: Wir möchten wissen, ob ein Studiengang einen wesentlichen Einfluss auf die Leistung der Studierenden bei einer bestimmten Prüfung hat. Um dies zu testen, bitten wir 20 Schüler einer Klasse, einen Vortest zu machen. Dann lassen wir jeden Schüler zwei Wochen lang am Lehrplan teilnehmen. Anschließend wiederholen die Schüler einen Test mit ähnlichem Schwierigkeitsgrad.

Der folgende Screenshot zeigt, wie ein gepaarter Stichproben-T-Test durchgeführt wird, um die Differenz zwischen den Durchschnittswerten des ersten und zweiten Tests zu vergleichen:

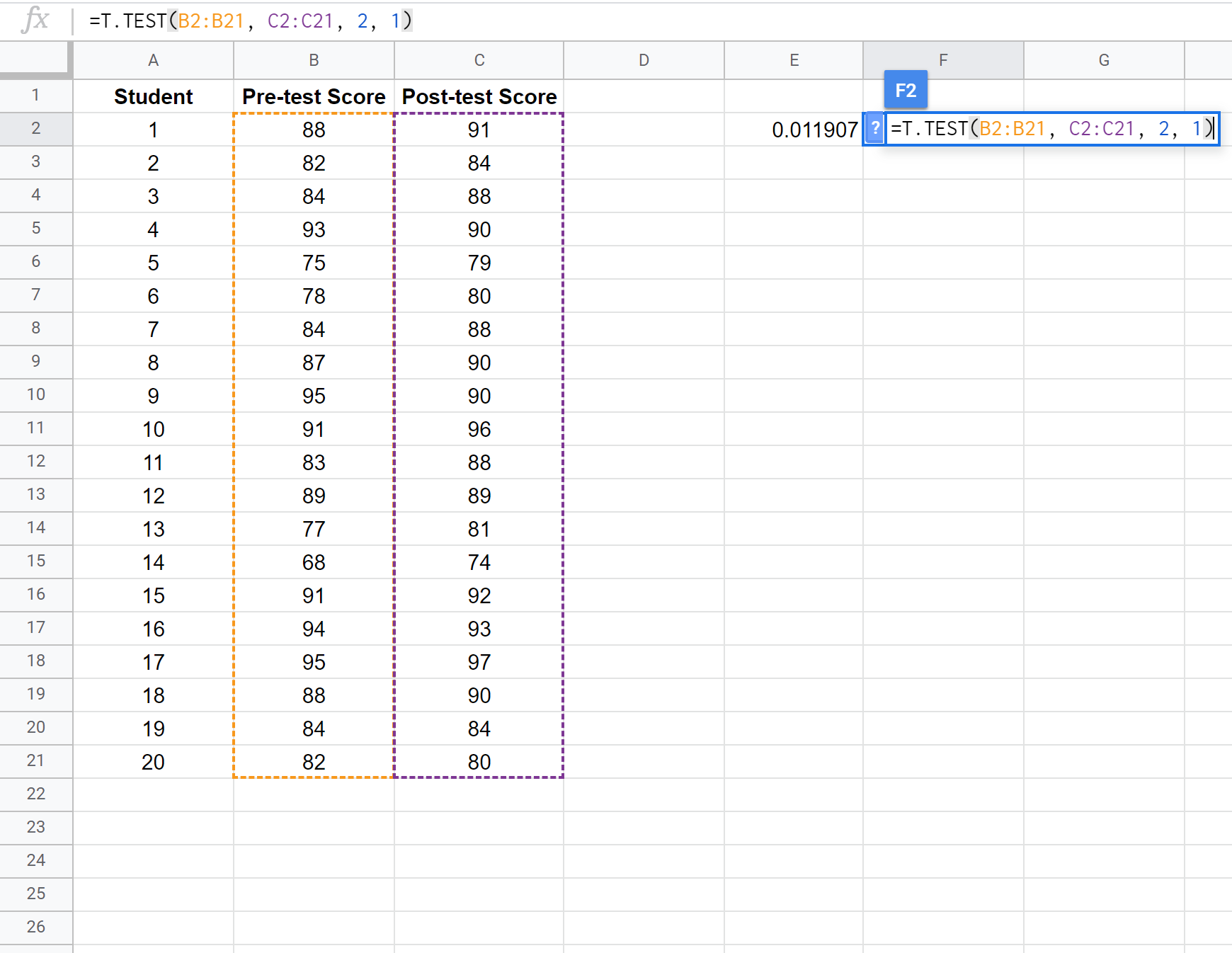
Hinweis: Es ist auch möglich, einen einseitigen t-Test bei zwei Stichproben mit oder ohne der Annahme durchzuführen, dass die beiden Stichproben die gleiche Varianz aufweisen. Informationen zum Anpassen der Testannahmen finden Sie in der T.TEST-Dokumentation .

Die beiden Annahmen für diesen T-Test für gepaarte Stichproben sind:

H ₀ : μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)

H ₁ : μ ₁ ≠ μ ₂ (die beiden Populationsmittelwerte sind nicht gleich)

Da der p-Wert unseres Tests (0,011907) kleiner als Alpha = 0,05 ist, lehnen wir die Nullhypothese des Tests ab. Wir haben genügend Belege dafür, dass es einen statistisch signifikanten Unterschied zwischen dem Durchschnittswert vor und nach dem Test gibt.