So berechnen sie z-scores in google sheets

In der Statistik sagt uns ein Z-Score , wie viele Standardabweichungen ein Wert vom Mittelwert hat . Wir verwenden die folgende Formel, um einen Z-Score zu berechnen:

z = (X – μ) / σ

Gold:

• X ist ein einzelner Rohdatenwert
• μ ist der Mittelwert des Datensatzes
• σ ist die Standardabweichung des Datensatzes

In diesem Tutorial wird erläutert, wie Sie Z-Scores für Rohdatenwerte in Google Sheets berechnen.

Beispiel: Z-Scores in Google Sheets

Angenommen, wir haben den folgenden Datensatz und möchten den Z-Score für jeden Rohdatenwert ermitteln:

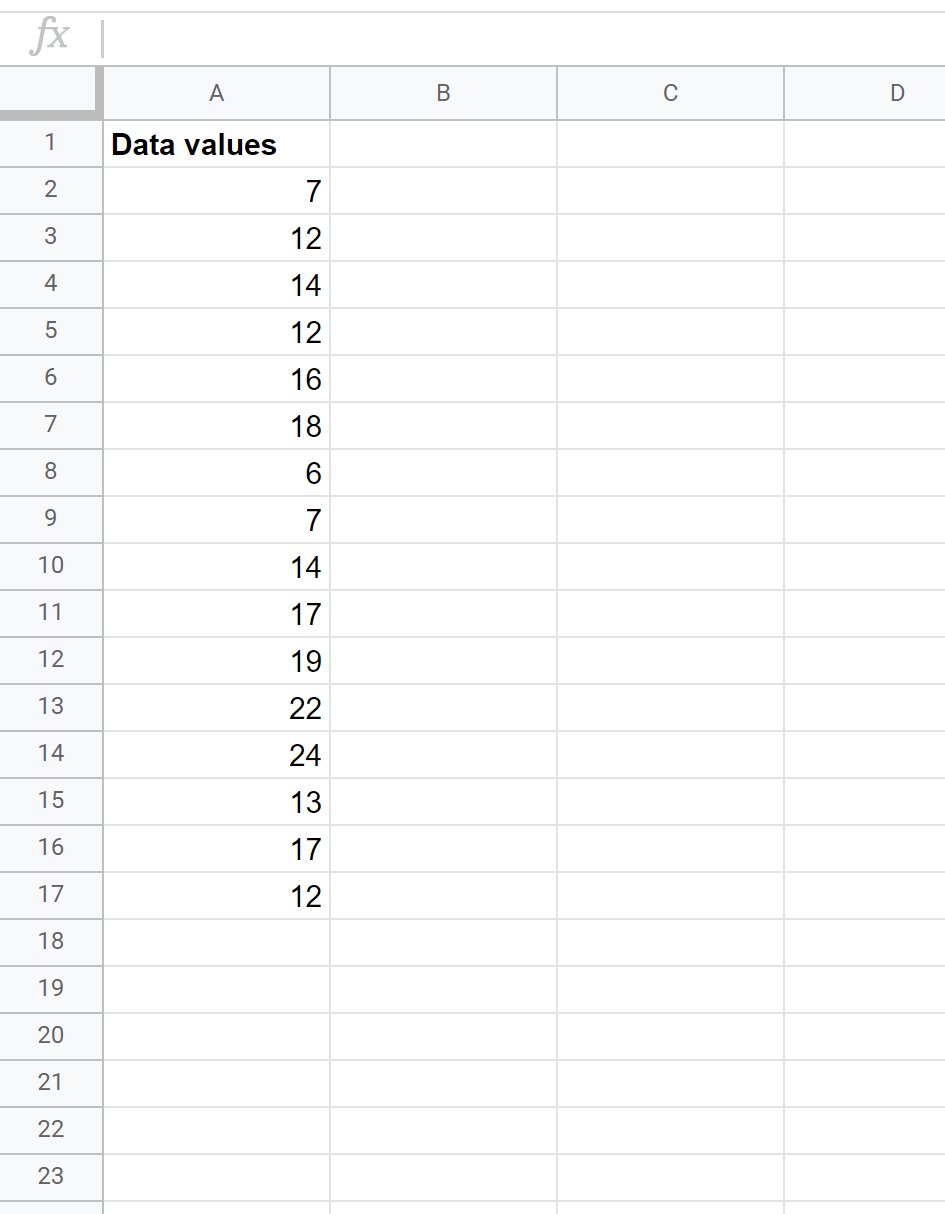
Dazu können wir die folgenden Schritte ausführen.

Schritt 1: Ermitteln Sie den Mittelwert und die Standardabweichung des Datensatzes.

Zuerst müssen wir den Mittelwert und die Standardabweichung des Datensatzes ermitteln. Die folgenden Formeln zeigen, wie das geht:

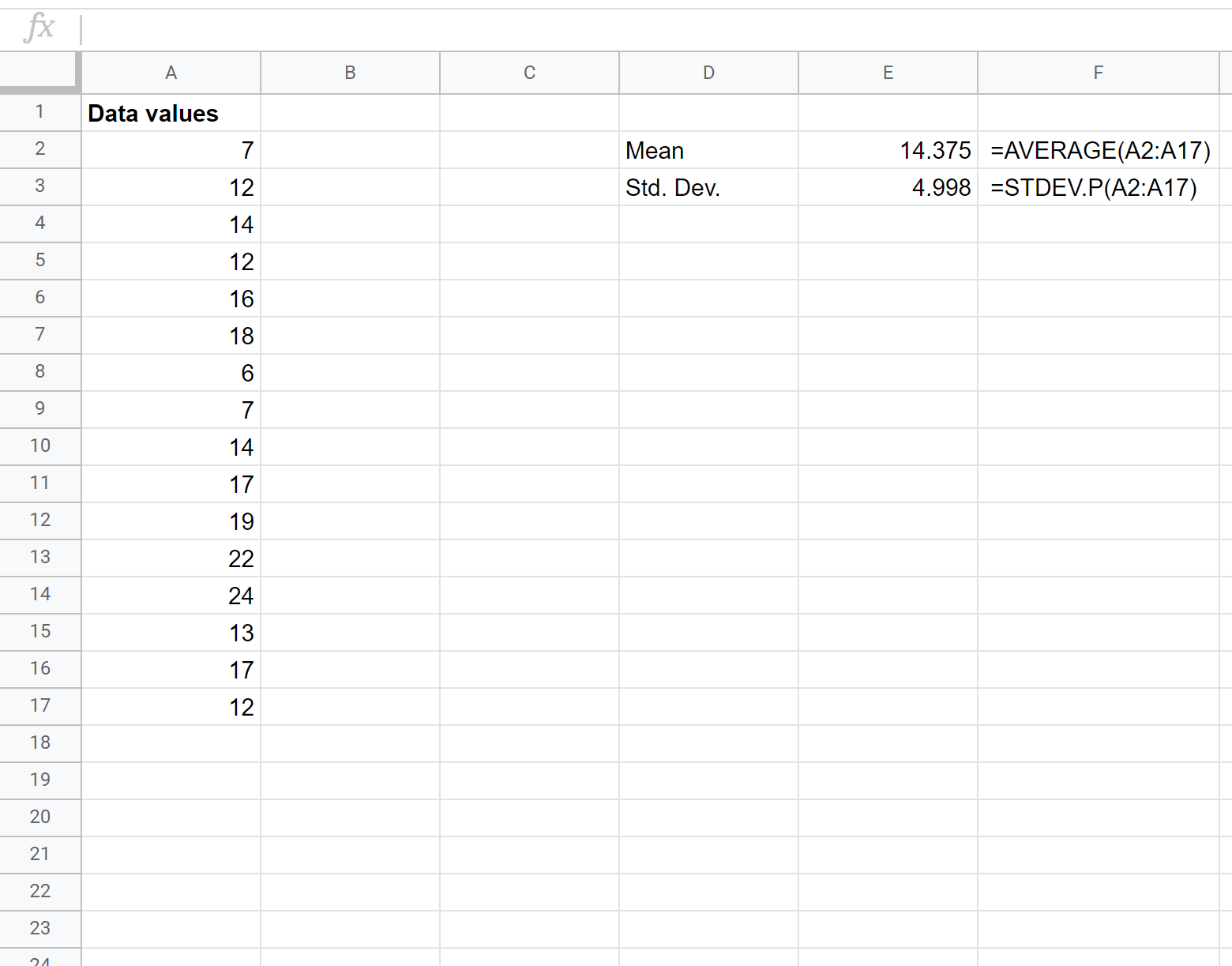
Der Mittelwert beträgt 14,375 und die Standardabweichung beträgt 4,998 .

Schritt 2: Ermitteln Sie den Z-Score für den ersten Rohdatenwert.

Als nächstes ermitteln wir den Z-Score für den ersten Rohdatenwert, indem wir die folgende Formel in Zelle B2 eingeben:

= ( A2 – $E$2 ) / $E$3

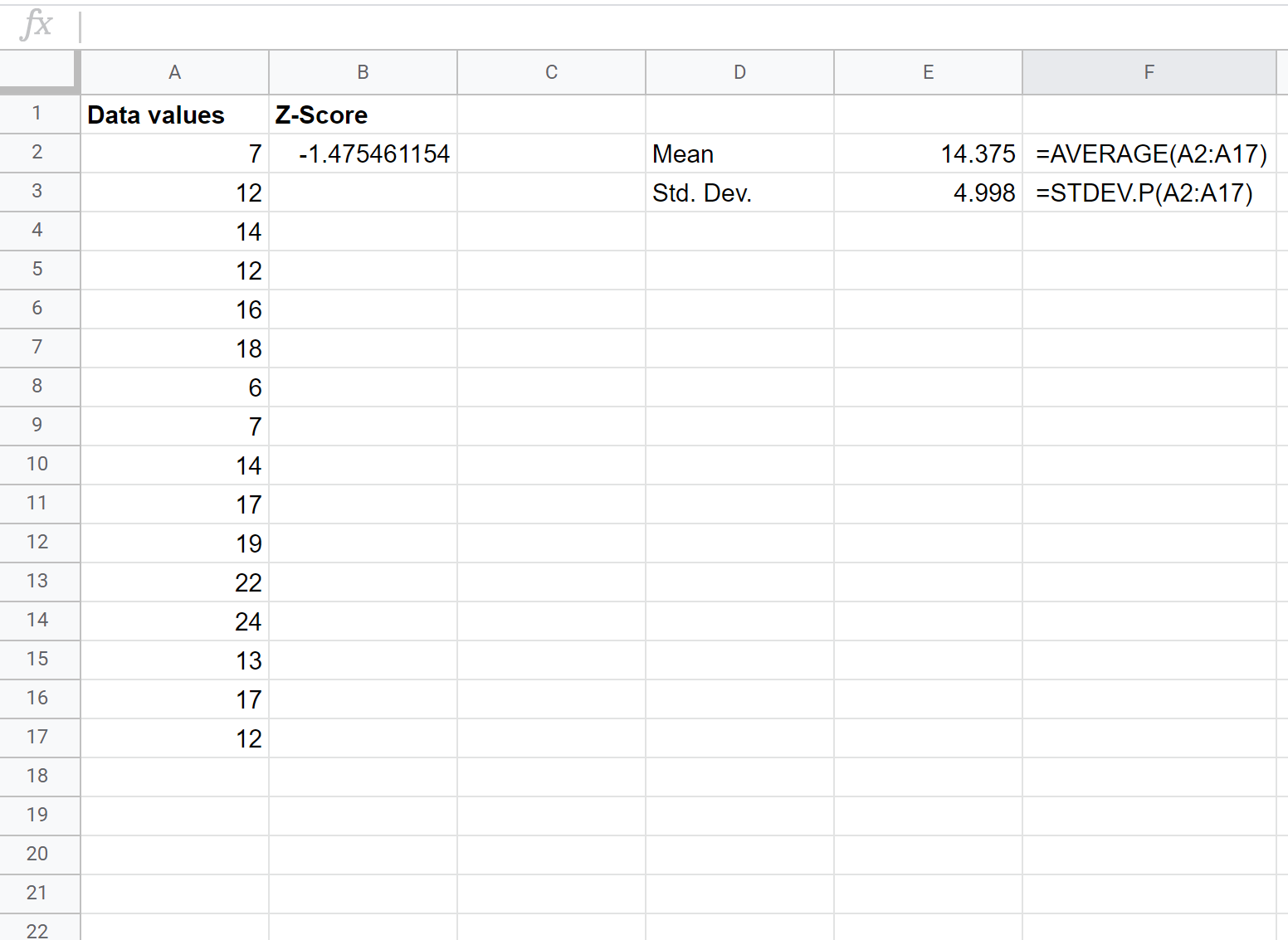
Schritt 3: Finden Sie die Z-Scores für alle verbleibenden Werte.

Sobald wir den ersten Z-Score berechnet haben, können wir den Rest von Spalte B, beginnend mit Zelle B2, markieren und Strg+D drücken, um die Formel von Zelle B2 in jede der folgenden Zellen zu kopieren:

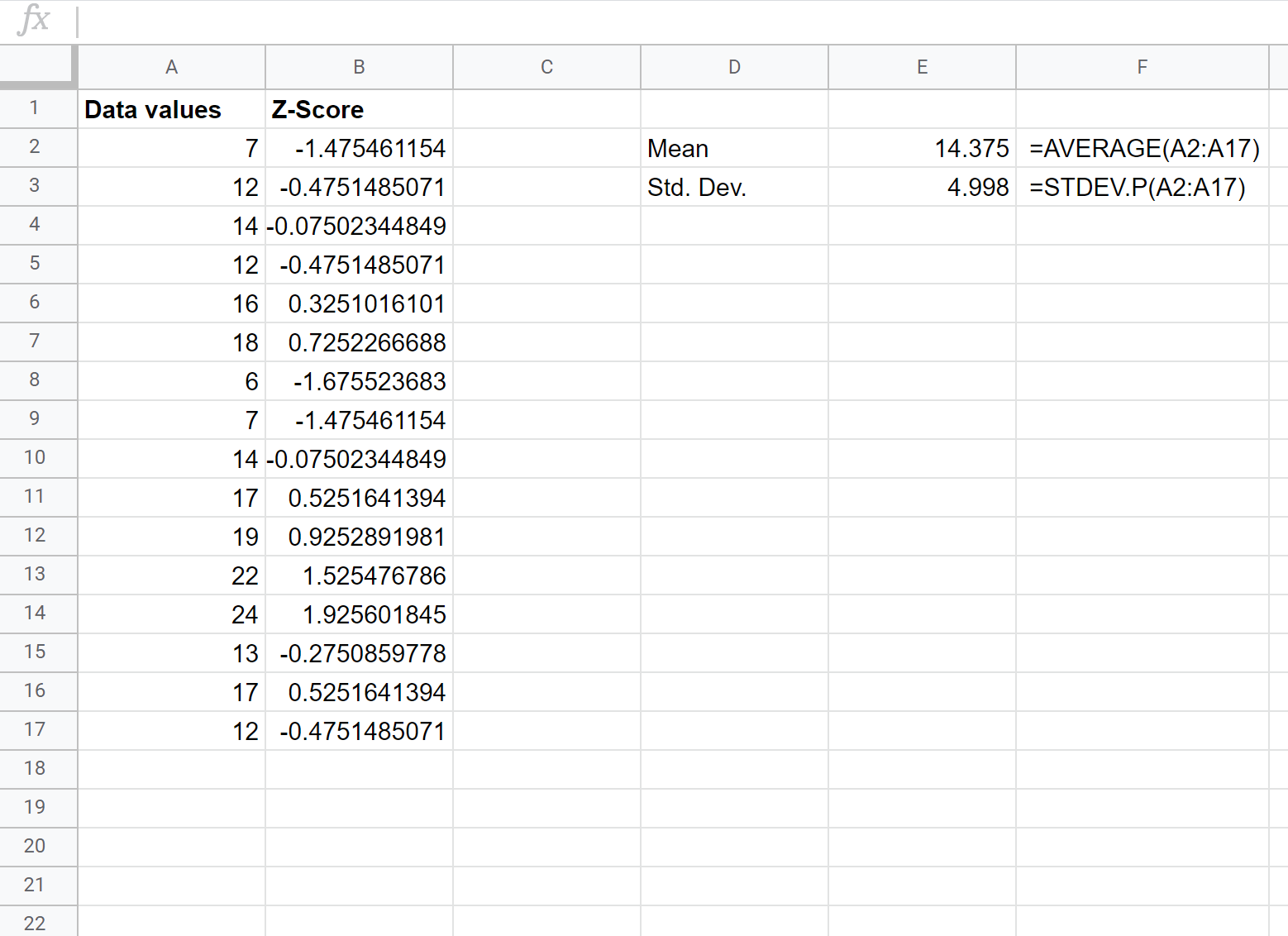
Wir haben jetzt den Z-Score für jeden Rohdatenwert gefunden.

So interpretieren Sie Z-Scores

Ein Z-Score sagt uns einfach, wie viele Standardabweichungen ein Wert vom Mittelwert hat.

In unserem Beispiel haben wir festgestellt, dass der Mittelwert 14,375 und die Standardabweichung 4,998 betrug.

Der erste Wert in unserem Datensatz war also 7, was einen Z-Score von (7-14,375) / 4,998 = -1,47546 hatte. Das bedeutet, dass der Wert „7“ um -1,47545 Standardabweichungen niedriger ist als der Mittelwert.

Der nächste Wert in unseren Daten, 12, hatte einen Z-Score von (12-14,375) / 4,998 = -0,47515 . Das bedeutet, dass der Wert „12“ um -0,47515 Standardabweichungen niedriger ist als der Mittelwert.

Je weiter ein Wert vom Mittelwert entfernt ist, desto höher ist der absolute Wert des Z-Scores für diesen Wert. Beispielsweise ist der Wert 7 weiter vom Mittelwert (14,375) entfernt als der Wert 12, was erklärt, warum 7 einen Z-Score mit einem größeren Absolutwert hatte.

Zusätzliche Ressourcen

So berechnen Sie Z-Scores in Excel
So berechnen Sie Z-Scores in R
So berechnen Sie Z-Scores auf einem TI-84-Rechner