So führen sie einen shapiro-wilk-test in r durch (mit beispielen)

Der Shapiro-Wilk-Test ist ein Normalitätstest. Es wird verwendet, um zu bestimmen, ob eine Stichprobe aus einerNormalverteilung stammt oder nicht.

Diese Art von Test ist nützlich, um festzustellen, ob ein bestimmter Datensatz aus einer Normalverteilung stammt oder nicht. Dies ist eine häufig verwendete Annahme in vielen statistischen Tests, einschließlich Regression , ANOVA , T-Tests und vielen anderen. ‚Andere.

Mit der folgenden integrierten Funktion in R können wir ganz einfach einen Shapiro-Wilk-Test für einen bestimmten Datensatz durchführen:

shapiro.test(x)

Gold:

• x: ein numerischer Vektor von Datenwerten.

Diese Funktion erzeugt eine W- Teststatistik zusammen mit einem entsprechenden p-Wert. Wenn der p-Wert kleiner als α = 0,05 ist, gibt es genügend Beweise dafür, dass die Stichprobe nicht aus einer normalverteilten Grundgesamtheit stammt.

Hinweis: Die Stichprobengröße muss zwischen 3 und 5.000 liegen, um die Funktion shapiro.test() verwenden zu können.

Dieses Tutorial zeigt einige Beispiele für die praktische Verwendung dieser Funktion.

Beispiel 1: Shapiro-Wilk-Test mit normalen Daten

Der folgende Code zeigt, wie ein Shapiro-Wilk-Test für einen Datensatz mit der Stichprobengröße n=100 durchgeführt wird:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.98957, p-value = 0.6303

Der p-Wert des Tests beträgt 0,6303 . Da dieser Wert nicht kleiner als 0,05 ist, können wir davon ausgehen, dass die Stichprobendaten aus einer normalverteilten Grundgesamtheit stammen.

Dieses Ergebnis sollte nicht überraschen, da wir die Beispieldaten mit der Funktion rnorm() generiert haben, die Zufallswerte aus einer Normalverteilung mit Mittelwert = 0 und Standardabweichung = 1 generiert.

Verwandt: Eine Anleitung zu dnorm, pnorm, qnorm und rnorm in R

Wir können auch ein Histogramm erstellen, um visuell zu überprüfen, ob die Beispieldaten normalverteilt sind:

 hist(data, col=' steelblue ') 

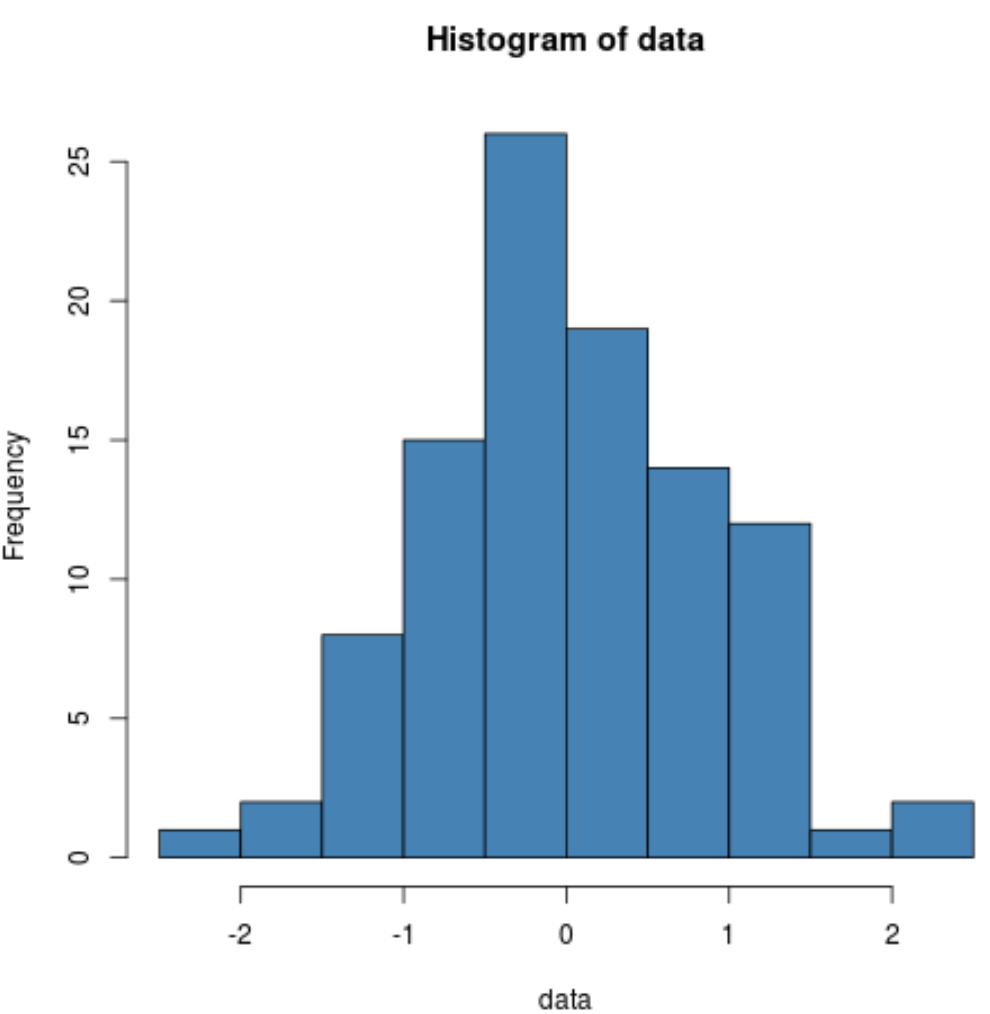
Wir können sehen, dass die Verteilung ziemlich glockenförmig ist und einen Peak in der Mitte der Verteilung aufweist, was typisch für normalverteilte Daten ist.

Beispiel 2: Shapiro-Wilk-Test für nicht normale Daten

Der folgende Code zeigt, wie man einen Shapiro-Wilk-Test für einen Datensatz mit der Stichprobengröße n=100 durchführt, bei dem die Werte zufällig aus einerPoisson-Verteilung generiert werden:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.94397, p-value = 0.0003393

Der p-Wert des Tests beträgt 0,0003393 . Da dieser Wert unter 0,05 liegt, haben wir genügend Beweise dafür, dass die Stichprobendaten nicht aus einer normalverteilten Grundgesamtheit stammen.

Dieses Ergebnis sollte nicht überraschen, da wir die Beispieldaten mit der Funktion rpois() generiert haben, die Zufallswerte aus einer Poisson-Verteilung generiert.

Verwandt: Eine Anleitung zu dpois, ppois, qpois und rpois in R

Wir können auch ein Histogramm erstellen, um visuell zu erkennen, dass die Beispieldaten nicht normalverteilt sind:

 hist(data, col=' coral2 ') 

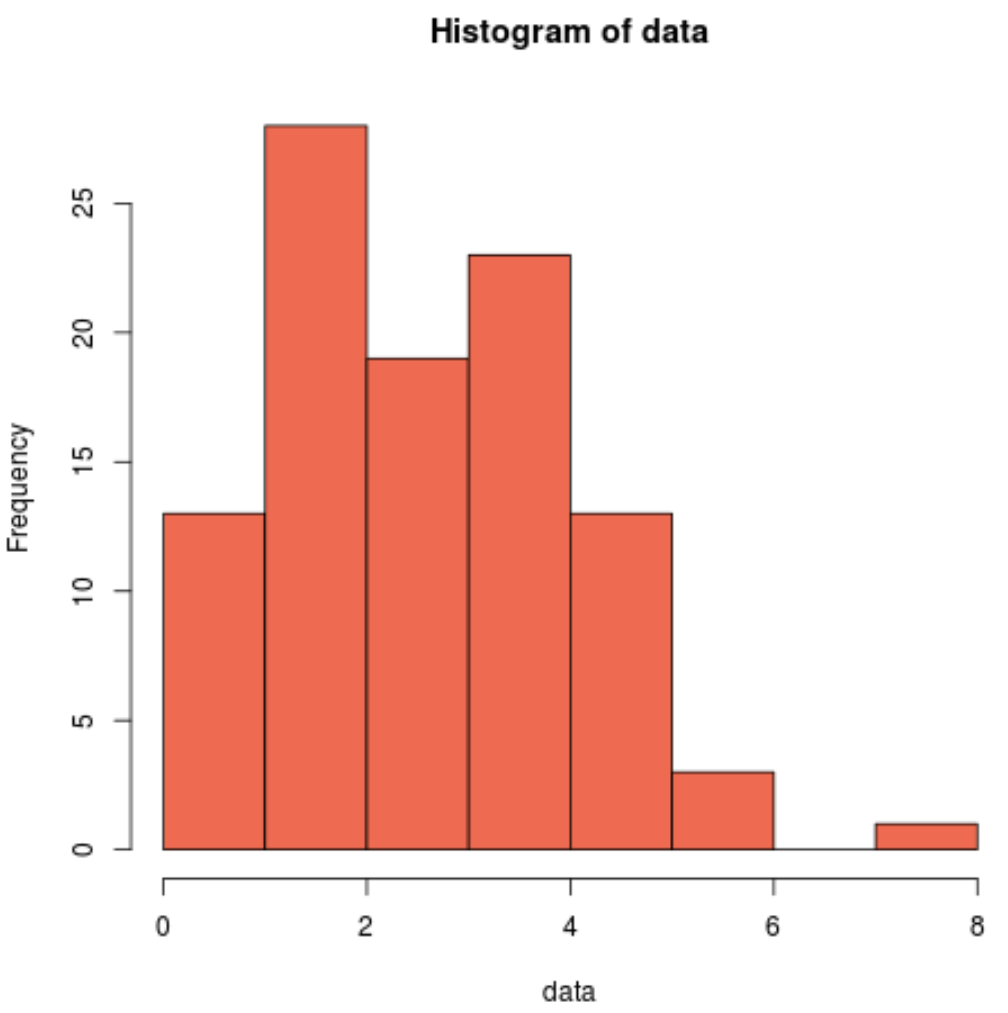
Wir können sehen, dass die Verteilung rechtsschief ist und nicht die typische „Glockenform“ einer Normalverteilung aufweist. Somit stimmt unser Histogramm mit den Ergebnissen des Shapiro-Wilk-Tests überein und bestätigt, dass unsere Stichprobendaten nicht aus einer Normalverteilung stammen.

Was tun mit nicht normalen Daten?

Wenn ein bestimmter Datensatz nicht normalverteilt ist , können wir häufig eine der folgenden Transformationen durchführen, um ihn normaler zu machen:

1. Log-Transformation: Transformieren Sie die Antwortvariable von y in log(y) .

2. Quadratwurzeltransformation: Transformieren Sie die Antwortvariable von y in √y .

3. Kubikwurzeltransformation: Transformieren Sie die Antwortvariable von y in y ^1/3 .

Durch die Durchführung dieser Transformationen nähert sich die Antwortvariable im Allgemeinen der Normalverteilung an.

Sehen Sie sichdieses Tutorial an, um zu erfahren, wie Sie diese Transformationen in der Praxis durchführen.

Zusätzliche Ressourcen

So führen Sie einen Anderson-Darling-Test in R durch
So führen Sie einen Kolmogorov-Smirnov-Test in R durch
So führen Sie einen Shapiro-Wilk-Test in Python durch