Was ist der bias-varianz-kompromiss beim maschinellen lernen?

Um die Leistung eines Modells anhand eines Datensatzes zu bewerten, müssen wir messen, wie gut die Vorhersagen des Modells mit den beobachteten Daten übereinstimmen.

Für Regressionsmodelle ist die am häufigsten verwendete Metrik der mittlere quadratische Fehler (MSE), der wie folgt berechnet wird:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Gold:

• n: Gesamtzahl der Beobachtungen
• y _i : Der Antwortwert der ^i-ten Beobachtung
• f( _xi ): Der vorhergesagte Antwortwert der i- ^ten Beobachtung

Je näher die Modellvorhersagen an den Beobachtungen liegen, desto niedriger ist der MSE.

Wir kümmern uns jedoch nur um den MSE-Test – den MSE, wenn unser Modell auf unsichtbare Daten angewendet wird. Dies liegt daran, dass uns nur die Leistung des Modells bei unbekannten Daten wichtig ist, nicht bei vorhandenen Daten.

Es ist zum Beispiel in Ordnung, wenn ein Modell, das Aktienkurse vorhersagt, einen niedrigen MSE für historische Daten aufweist, wir möchten das Modell jedoch wirklich verwenden können, um zukünftige Daten genau vorherzusagen.

Es stellt sich heraus, dass der MSE-Test immer noch in zwei Teile unterteilt werden kann:

(1) Varianz: bezieht sich auf den Betrag, um den sich unsere Funktion f ändern würde, wenn wir sie mit einem anderen Trainingssatz schätzen würden.

(2) Bias: bezieht sich auf den Fehler, der dadurch entsteht, dass ein reales Problem, das äußerst kompliziert sein kann, mit einem viel einfacheren Modell angegangen wird.

In mathematischen Begriffen geschrieben:

MSE-Test = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE-Test = Varianz + Bias ² + irreduzibler Fehler

Der dritte Term, der irreduzible Fehler, ist der Fehler, der von keinem Modell reduziert werden kann, einfach weil die Beziehung zwischen dem Satz erklärender Variablen und der Antwortvariablen immer ein Rauschen aufweist.

Modelle mit hoher Verzerrung weisen tendenziell eine geringe Varianz auf. Beispielsweise neigen lineare Regressionsmodelle zu einer hohen Verzerrung (unter der Annahme einer einfachen linearen Beziehung zwischen den erklärenden Variablen und der Antwortvariablen) und einer geringen Varianz (die Modellschätzungen ändern sich von Stichprobe zu Stichprobe nicht wesentlich). das andere).

Allerdings weisen Modelle mit geringer Verzerrung tendenziell eine hohe Varianz auf. Beispielsweise neigen komplexe nichtlineare Modelle zu einer geringen Verzerrung (es wird keine bestimmte Beziehung zwischen den erklärenden Variablen und der Antwortvariablen angenommen) und einer hohen Varianz (Modellschätzungen können sich von einer Lernstichprobe zur anderen erheblich ändern).

Der Bias-Varianz-Kompromiss

Der Kompromiss zwischen Bias und Varianz bezieht sich auf den Kompromiss, der stattfindet, wenn wir uns dafür entscheiden, den Bias zu reduzieren, was im Allgemeinen die Varianz erhöht, oder die Varianz zu verringern, was im Allgemeinen den Bias erhöht.

Die folgende Grafik bietet eine Möglichkeit, diesen Kompromiss zu visualisieren:

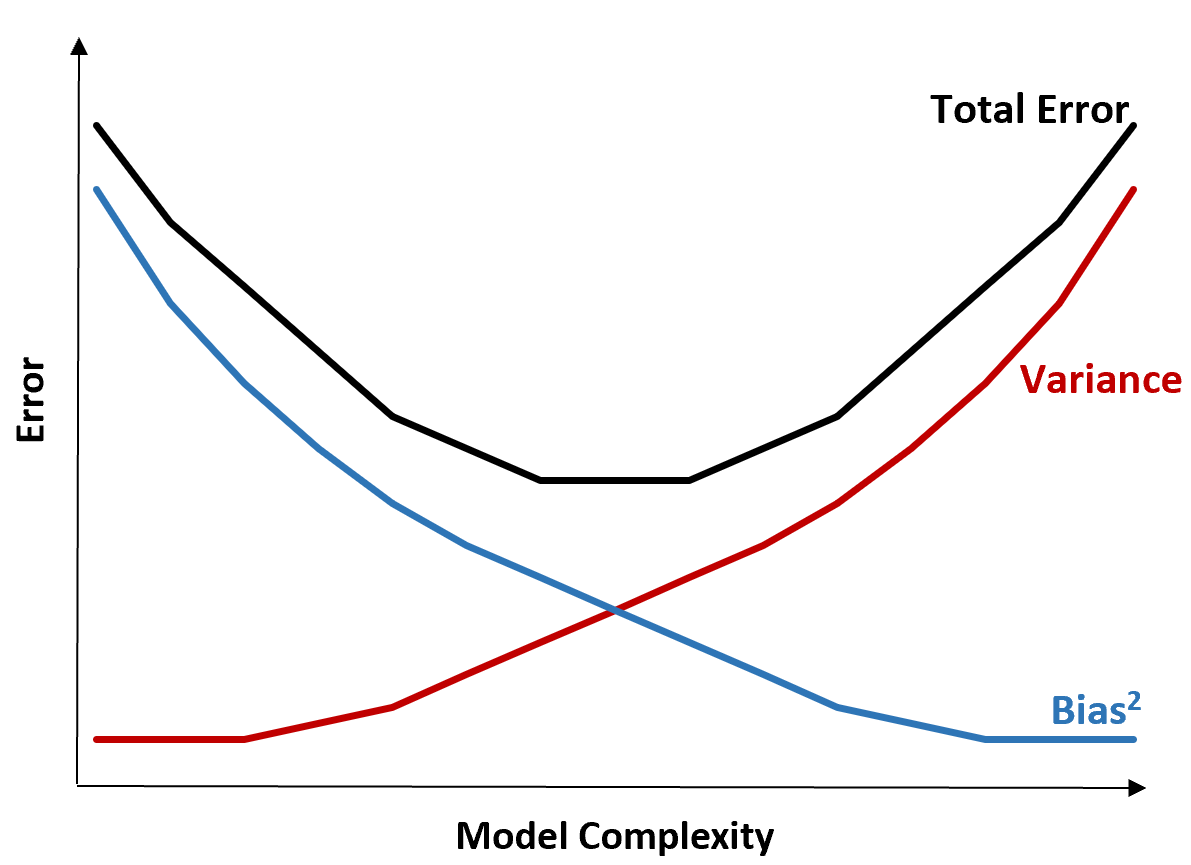
Der Gesamtfehler nimmt mit zunehmender Komplexität eines Modells ab, jedoch nur bis zu einem bestimmten Punkt. Ab einem bestimmten Punkt beginnt die Varianz zuzunehmen und auch der Gesamtfehler beginnt zuzunehmen.

In der Praxis geht es uns nur um die Minimierung des Gesamtfehlers eines Modells, nicht unbedingt um die Minimierung der Varianz oder Verzerrung. Es stellt sich heraus, dass der Weg zur Minimierung des Gesamtfehlers darin besteht, das richtige Gleichgewicht zwischen Varianz und Bias zu finden.

Mit anderen Worten: Wir wollen ein Modell, das komplex genug ist, um die wahre Beziehung zwischen den erklärenden Variablen und der Antwortvariablen zu erfassen, aber nicht zu komplex, um Muster zu erkennen, die tatsächlich nicht existieren.

Wenn ein Modell zu komplex ist, passt es die Daten zu stark an. Dies liegt daran, dass es zu schwierig ist, Muster in den Trainingsdaten zu finden, die einfach durch Zufall entstanden sind. Diese Art von Modell wird bei unsichtbaren Daten wahrscheinlich eine schlechte Leistung erbringen.

Wenn ein Modell jedoch zu einfach ist, unterschätzt es die Daten. Dies geschieht, weil davon ausgegangen wird, dass die wahre Beziehung zwischen den erklärenden Variablen und der Antwortvariablen einfacher ist, als sie tatsächlich ist.

Der Weg zur Auswahl optimaler Modelle beim maschinellen Lernen besteht darin, ein Gleichgewicht zwischen Bias und Varianz zu finden, um den Fehler beim Testen des Modells anhand zukünftiger, unsichtbarer Daten zu minimieren.

In der Praxis ist die Kreuzvalidierung die häufigste Methode zur Minimierung der MSE von Tests.