So führen sie eine logistische regression in python durch (schritt für schritt)

Die logistische Regression ist eine Methode, mit der wir ein Regressionsmodell anpassen können, wenn die Antwortvariable binär ist.

Die logistische Regression verwendet eine als Maximum-Likelihood-Schätzung bekannte Methode, um eine Gleichung der folgenden Form zu finden:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Gold:

• X _j : die j ^-te Vorhersagevariable
• β _j : Schätzung des Koeffizienten für die j ^-te Vorhersagevariable

Die Formel auf der rechten Seite der Gleichung sagt die logarithmische Wahrscheinlichkeit voraus, dass die Antwortvariable den Wert 1 annimmt.

Wenn wir also ein logistisches Regressionsmodell anpassen, können wir die folgende Gleichung verwenden, um die Wahrscheinlichkeit zu berechnen, dass eine bestimmte Beobachtung den Wert 1 annimmt:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Anschließend verwenden wir einen bestimmten Wahrscheinlichkeitsschwellenwert, um die Beobachtung als 1 oder 0 zu klassifizieren.

Beispielsweise könnten wir sagen, dass Beobachtungen mit einer Wahrscheinlichkeit größer oder gleich 0,5 als „1“ und alle anderen Beobachtungen als „0“ klassifiziert werden.

Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung einer logistischen Regression in R.

Schritt 1: Importieren Sie die erforderlichen Pakete

Zuerst importieren wir die notwendigen Pakete, um eine logistische Regression in Python durchzuführen:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Schritt 2: Daten laden

Für dieses Beispiel verwenden wir den Standarddatensatz aus dem Buch Introduction to Statistical Learning . Mit dem folgenden Code können wir eine Zusammenfassung des Datensatzes laden und anzeigen:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

Dieser Datensatz enthält die folgenden Informationen zu 10.000 Personen:

• Standard: Gibt an, ob eine Person in Verzug geraten ist oder nicht.
• Student: gibt an, ob eine Person Student ist oder nicht.
• Guthaben: Durchschnittliches Guthaben einer Person.
• Einkommen: Einkommen des Einzelnen.

Wir werden Studentenstatus, Bankguthaben und Einkommen verwenden, um ein logistisches Regressionsmodell zu erstellen, das die Wahrscheinlichkeit vorhersagt, dass eine bestimmte Person zahlungsunfähig wird.

Schritt 3: Erstellen Sie Trainings- und Testbeispiele

Als Nächstes teilen wir den Datensatz in einen Trainingssatz zum Trainieren des Modells und einen Testsatz zum Testen des Modells auf.

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

Schritt 4: Passen Sie das logistische Regressionsmodell an

Als Nächstes verwenden wir die Funktion LogisticRegression(), um ein logistisches Regressionsmodell an den Datensatz anzupassen:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

Schritt 5: Modelldiagnose

Sobald wir das Regressionsmodell angepasst haben, können wir die Leistung unseres Modells anhand des Testdatensatzes analysieren.

Zuerst erstellen wir die Verwirrungsmatrix für das Modell:

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

Aus der Verwirrungsmatrix können wir Folgendes ersehen:

• #Echt positive Vorhersagen: 2886
• #Echte negative Vorhersagen: 0
• #Falsch positive Vorhersagen: 113
• #Falsch negative Vorhersagen: 1

Wir können auch das Genauigkeitsmodell abrufen, das uns den Prozentsatz der vom Modell getroffenen Korrekturvorhersagen angibt:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

Dies sagt uns, dass das Modell in 96,2 % der Fälle die richtige Vorhersage darüber getroffen hat, ob eine Person ausfallen würde oder nicht.

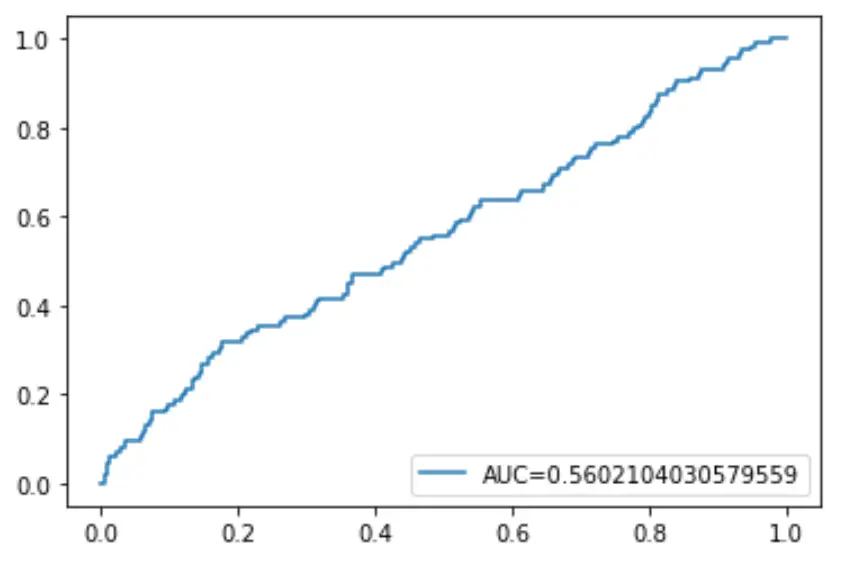
Schließlich können wir die ROC-Kurve (Receiver Operating Characteristic) zeichnen, die den Prozentsatz der vom Modell vorhergesagten echten positiven Ergebnisse anzeigt, wenn der Schwellenwert für die Vorhersagewahrscheinlichkeit von 1 auf 0 gesenkt wird.

Je höher die AUC (Fläche unter der Kurve) ist, desto genauer kann unser Modell die Ergebnisse vorhersagen:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()