Was ist überanpassung beim maschinellen lernen? (erklärung & beispiele)

Beim maschinellen Lernen erstellen wir häufig Modelle, um genaue Vorhersagen über bestimmte Phänomene treffen zu können.

Angenommen, wir möchten ein Regressionsmodell erstellen, das die Prädiktorvariable Lernstunden verwendet, um den ACT-Score der Antwortvariable für Oberstufenschüler vorherzusagen.

Um dieses Modell zu erstellen, sammeln wir Daten über die Lernstunden und den entsprechenden ACT-Score für Hunderte von Schülern in einem bestimmten Schulbezirk.

Anschließend werden wir diese Daten verwenden, um ein Modell zu trainieren , das Vorhersagen über die Punktzahl treffen kann, die ein bestimmter Schüler basierend auf der Gesamtzahl der gelernten Stunden erhalten wird.

Um den Nutzen des Modells zu beurteilen, können wir messen, wie gut die Vorhersagen des Modells mit den beobachteten Daten übereinstimmen. Eine der am häufigsten verwendeten Metriken hierfür ist der mittlere quadratische Fehler (MSE), der wie folgt berechnet wird:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Gold:

• n: Gesamtzahl der Beobachtungen
• y _i : Der Antwortwert der ^i-ten Beobachtung
• f( _xi ): Der vorhergesagte Antwortwert der i- ^ten Beobachtung

Je näher die Modellvorhersagen an den Beobachtungen liegen, desto niedriger ist der MSE.

Einer der größten Fehler beim maschinellen Lernen besteht jedoch darin, Modelle zu optimieren, um den Trainings-MSE zu reduzieren, d. h. wie gut die Modellvorhersagen mit den Daten übereinstimmen, die wir zum Trainieren des Modells verwendet haben.

Wenn sich ein Modell zu sehr auf die Reduzierung des Trainings-MSE konzentriert, arbeitet es oft zu sehr daran, Muster in den Trainingsdaten zu finden, die einfach durch Zufall verursacht werden. Wenn das Modell dann auf unsichtbare Daten angewendet wird, ist seine Leistung schlecht.

Dieses Phänomen wird als Überanpassung bezeichnet. Dies geschieht, wenn wir ein Modell zu eng an die Trainingsdaten „anpassen“ und so am Ende ein Modell erstellen, das für Vorhersagen auf neuen Daten nicht nützlich ist.

Beispiel für Überanpassung

Um die Überanpassung zu verstehen, kehren wir zum Beispiel der Erstellung eines Regressionsmodells zurück, das stundenlanges Lernen nutzt, um den ACT-Score vorherzusagen.

Nehmen wir an, wir sammeln Daten für 100 Schüler in einem bestimmten Schulbezirk und erstellen ein schnelles Streudiagramm, um die Beziehung zwischen den beiden Variablen zu veranschaulichen:

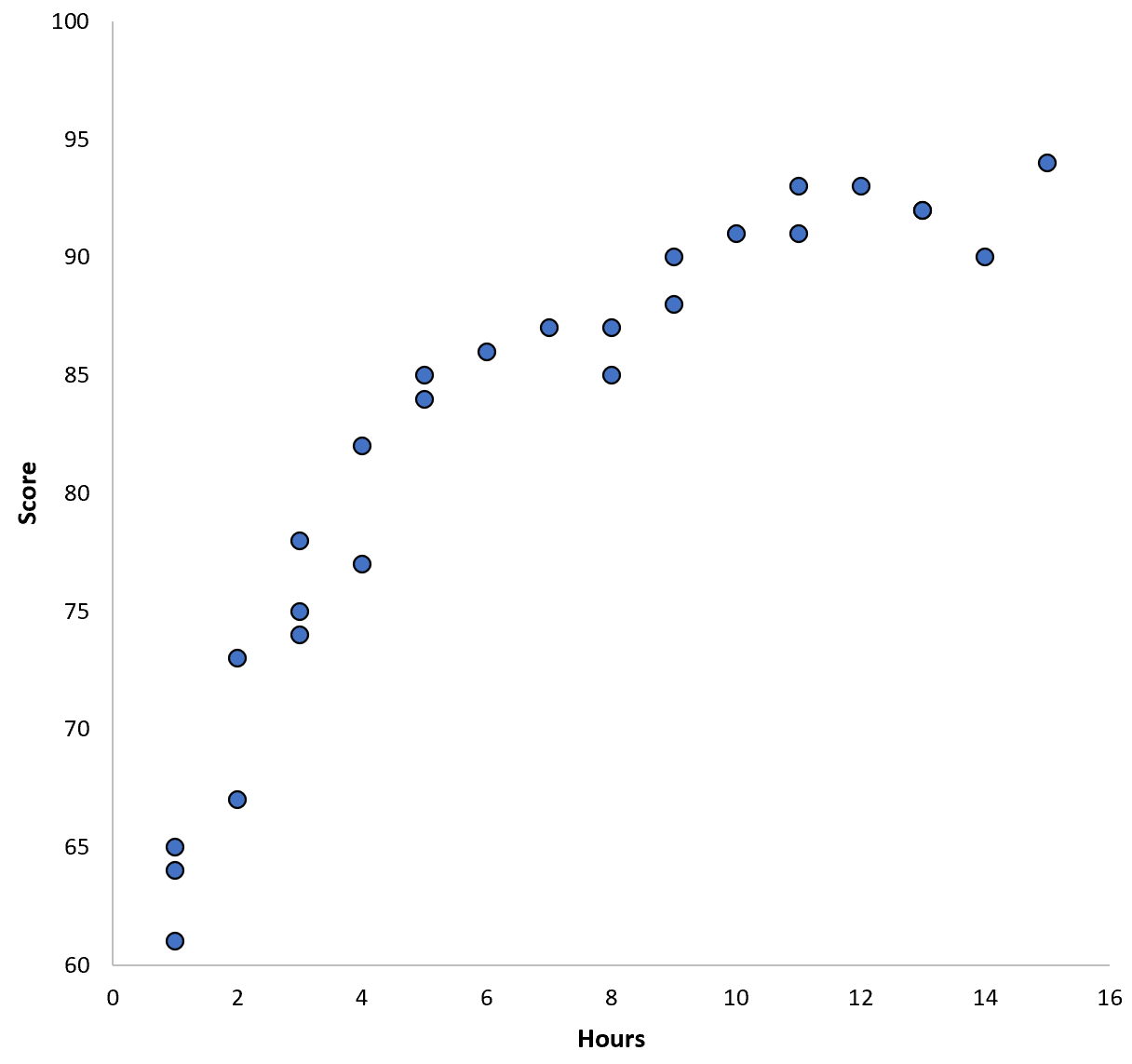
Die Beziehung zwischen den beiden Variablen scheint quadratisch zu sein. Nehmen wir also an, wir wenden das folgende quadratische Regressionsmodell an:

Punktzahl = 60,1 + 5,4*(Stunden) – 0,2*(Stunden) ²

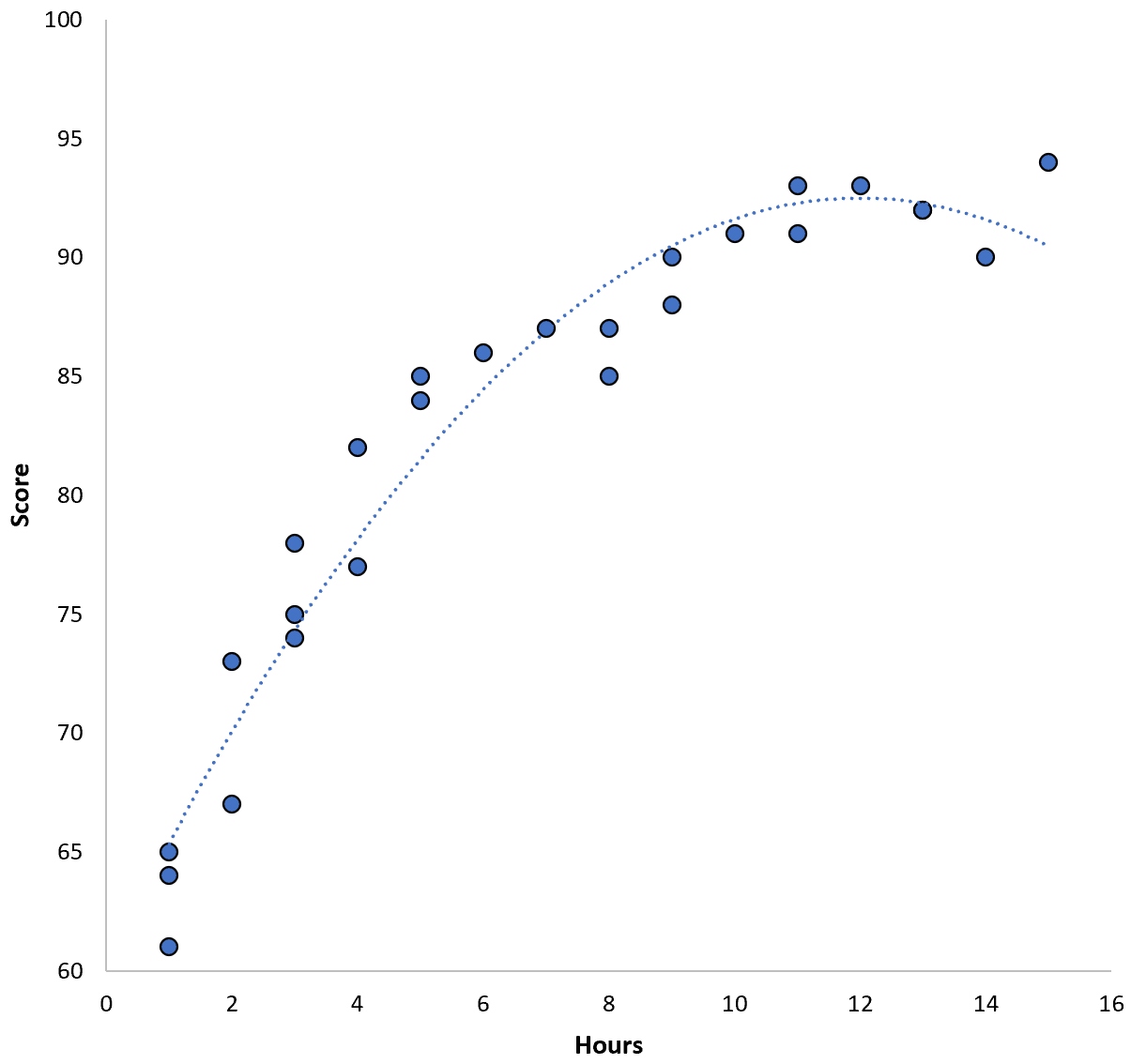
Dieses Modell hat einen mittleren quadratischen Trainingsfehler (MSE) von 3,45 . Das heißt, der quadratische Mittelwert der Differenz zwischen den Vorhersagen des Modells und den tatsächlichen ACT-Ergebnissen beträgt 3,45.

Wir könnten diese Trainings-MSE jedoch reduzieren, indem wir ein Polynommodell höherer Ordnung anpassen. Angenommen, wir wenden das folgende Modell an:

Punktzahl = 64,3 – 7,1*(Stunden) + 8,1*(Stunden) ² – 2,1*(Stunden) ³ + 0,2*(Stunden ^{) 4 – 0,1*(Stunden) 5 +} 0,2(Stunden) ⁶

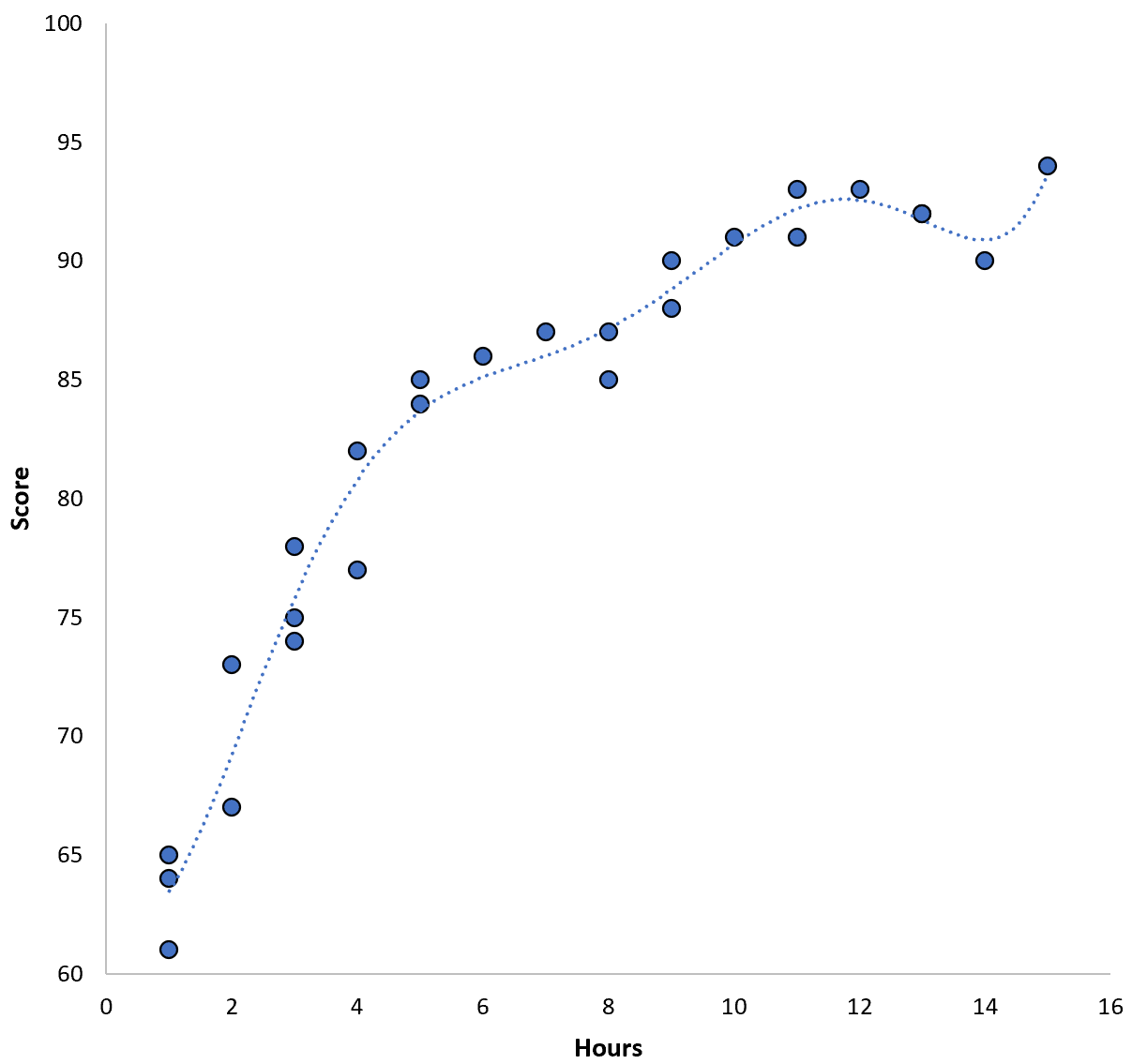
Beachten Sie, dass die Regressionslinie viel besser zu den tatsächlichen Daten passt als die vorherige Regressionslinie.

Dieses Modell hat einen quadratischen Trainingsfehler (MSE) von nur 0,89 . Das heißt, der quadratische Mittelwert der Differenz zwischen den Vorhersagen des Modells und den tatsächlichen ACT-Ergebnissen beträgt 0,89.

Dieses MSE-Training ist viel kleiner als das des Vorgängermodells.

Der Trainings-MSE ist uns jedoch egal, d. h. wie gut die Vorhersagen des Modells mit den Daten übereinstimmen, die wir zum Trainieren des Modells verwendet haben. Stattdessen kümmern wir uns hauptsächlich um den MSE-Test – den MSE, wenn unser Modell auf unsichtbare Daten angewendet wird.

Wenn wir das obige Polynom-Regressionsmodell höherer Ordnung auf einen unbekannten Datensatz anwenden würden, würde es wahrscheinlich schlechter abschneiden als das einfachere quadratische Regressionsmodell. Das heißt, es würde zu einem höheren MSE-Test führen, was genau das ist, was wir nicht wollen.

So erkennen und vermeiden Sie eine Überanpassung

Der einfachste Weg, eine Überanpassung zu erkennen, ist die Durchführung einer Kreuzvalidierung. Die am häufigsten verwendete Methode ist die k-fache Kreuzvalidierung und funktioniert wie folgt:

Schritt 1: Teilen Sie einen Datensatz zufällig in k Gruppen oder „Faltungen“ von ungefähr gleicher Größe auf.

Schritt 2: Wählen Sie eine der Falten als Halteset. Passen Sie die Schablone an die verbleibenden K-1-Falten an. Berechnen Sie den MSE-Test anhand der Beobachtungen in der gespannten Lage.

Schritt 3: Wiederholen Sie diesen Vorgang k -mal, wobei Sie jedes Mal einen anderen Satz als Ausschlusssatz verwenden.

Schritt 4: Berechnen Sie den Gesamt-MSE des Tests als Durchschnitt der k MSE des Tests.

Test MSE = (1/k)*ΣMSE _i

Gold:

• k: Anzahl der Falten
• MSE _i : Testen Sie MSE bei der ^i-ten Iteration

Dieser MSE-Test gibt uns eine gute Vorstellung davon, wie sich ein bestimmtes Modell bei unbekannten Daten verhält.

In der Praxis können wir mehrere verschiedene Modelle anpassen und für jedes Modell eine k-fache Kreuzvalidierung durchführen, um seinen MSE-Test herauszufinden. Wir können dann das Modell mit dem niedrigsten MSE-Test als bestes Modell für zukünftige Vorhersagen auswählen.

Dadurch wird sichergestellt, dass wir ein Modell auswählen, das bei zukünftigen Daten wahrscheinlich die beste Leistung erbringt, im Gegensatz zu einem Modell, das lediglich die Trainings-MSE minimiert und gut zu historischen Daten „passt“.

Zusätzliche Ressourcen

Was ist der Bias-Varianz-Kompromiss beim maschinellen Lernen?
Eine Einführung in die K-Fold-Kreuzvalidierung
Regressions- und Klassifizierungsmodelle im maschinellen Lernen