Sturges-regel
In diesem Artikel wird erklärt, was die Sturges-Regel ist und wie ihre Formel lautet. Außerdem finden Sie hier ein konkretes Schritt-für-Schritt-Beispiel zur Sturges-Regel und darüber hinaus einen Online-Rechner für die Sturges-Regel.
Was ist die Sturges-Regel?
Die Sturges-Regel ist eine Regel zur Berechnung der idealen Anzahl von Klassen oder Intervallen, in die ein Datensatz unterteilt werden sollte.
Die Formel für die Sturges-Regel besagt, dass die Anzahl der Klassen gleich eins plus dem Logarithmus zur Basis zwei der Gesamtzahl der Daten ist.
Gold
ist die Anzahl der Klassen oder Intervalle und
ist die Gesamtzahl der Beobachtungen in der Stichprobe.
Die meisten Rechner erlauben nur Berechnungen mit Logarithmen zur Basis 10. In diesem Fall können Sie diese äquivalente Formel verwenden:
Die Sturges-Regel wurde 1926 vom deutschen Statistiker Herbert Sturges erstellt.
Beispiel einer Sturges-Regel
Nachdem wir nun wissen, was die Sturges-Regel ist, werden wir anhand einer Schritt-für-Schritt-Übung sehen, wie die Intervalle eines Datensatzes mithilfe der Sturges-Regel in der Statistik berechnet werden.
- Die Stichprobengröße von 50 verschiedenen Personen wurde gemessen und alle Werte in der folgenden Datentabelle aufgezeichnet. Wenden Sie die Sturges-Regel an, um den Datensatz in Intervalle zu unterteilen, und zeichnen Sie die Daten dann in einem Histogramm auf.
Zuerst müssen wir die Daten in Intervalle unterteilen. Insgesamt gibt es 50 Datenelemente, daher verwenden wir die Sturges-Regel mit diesem Wert:
![\begin{array}{l}c=1+\log_2(N)\\[2ex]c=1+\log_2(50)\\[2ex]c=1+5,64\\[2ex]c=6,64\\[2ex]c\approx 7\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9929b0c8f1f7cdf5a6160c07e0205c46_l3.png "Rendered by QuickLaTeX.com")
Daher ist es notwendig, die Daten zu trennen und in sieben Intervalle zu gruppieren. Wir müssen nun die Breite jedes Intervalls kennen. Teilen Sie dazu einfach den Maximalwert minus dem Minimalwert durch die Gesamtzahl der Intervalle:
Kurz gesagt, es müssen 7 Intervalle mit einer Amplitude von 9 vorhanden sein, sodass die mit der Sturges-Methode berechneten Intervalle wie folgt lauten:
Nachdem wir die Intervalle berechnet haben, müssen wir zählen, wie oft ein Datenelement in jedem Intervall erscheint, und die Häufigkeitstabelle erstellen:
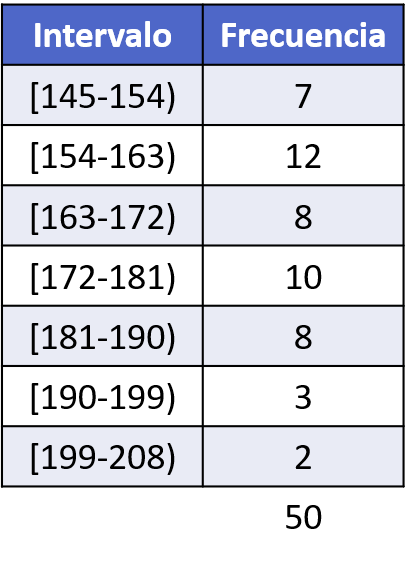
Schließlich können wir aus der Häufigkeitstabelle das Histogramm erstellen, um die Daten grafisch darzustellen:
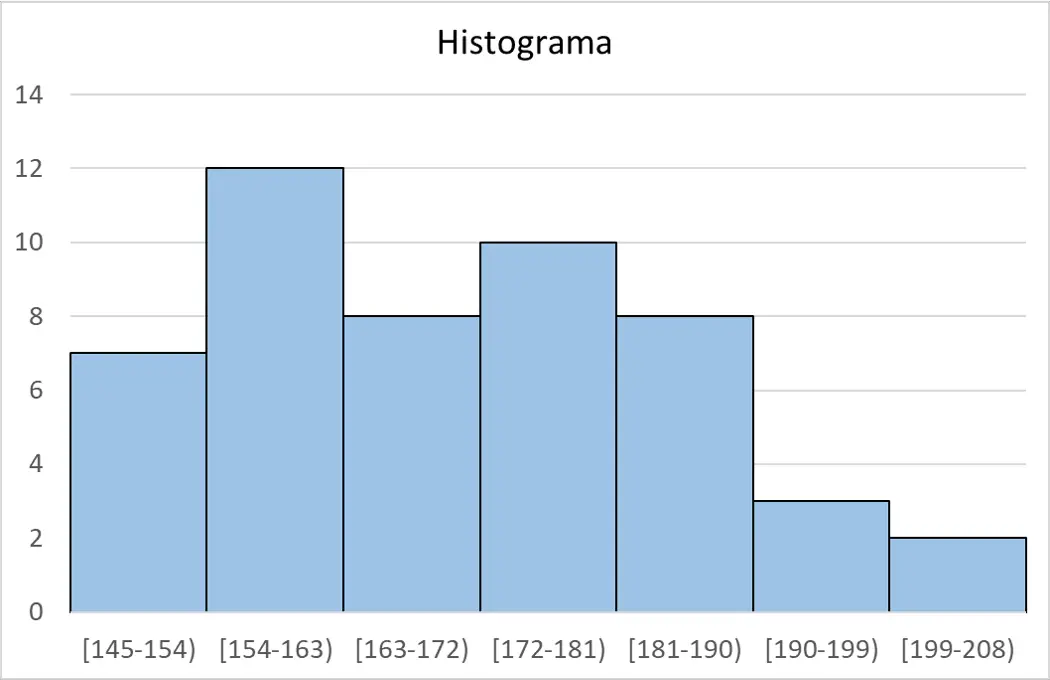
Sturges-Regelrechner
Geben Sie die Gesamtzahl der Datenproben ein und klicken Sie auf „Berechnen“, dann gibt der Rechner die Anzahl der gemäß der Sturges-Regel berechneten Intervalle zurück.
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen