Ridge-regression in r (schritt für schritt)
Die Ridge-Regression ist eine Methode, mit der wir ein Regressionsmodell anpassen können, wenn in den Daten Multikollinearität vorhanden ist.
Kurz gesagt versucht die Regression der kleinsten Quadrate, Koeffizientenschätzungen zu finden, die die verbleibende Quadratsumme (RSS) minimieren:
RSS = Σ(y i – ŷ i )2
Gold:
- Σ : Ein griechisches Symbol für Summe
- y i : der tatsächliche Antwortwert für die i-te Beobachtung
- ŷ i : Der vorhergesagte Antwortwert basierend auf dem multiplen linearen Regressionsmodell
Umgekehrt versucht die Ridge-Regression Folgendes zu minimieren:
RSS + λΣβ j 2
wobei j von 1 zu p Prädiktorvariablen geht und λ ≥ 0 ist.
Dieser zweite Term in der Gleichung wird als Auszahlungsstrafe bezeichnet. Bei der Ridge-Regression wählen wir einen Wert für λ, der den geringstmöglichen MSE-Test (mittlerer quadratischer Fehler) ergibt.
Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung einer Ridge-Regression in R.
Schritt 1: Daten laden
Für dieses Beispiel verwenden wir den integrierten Datensatz von R namens mtcars . Wir werden hp als Antwortvariable und die folgenden Variablen als Prädiktoren verwenden:
- mpg
- Gewicht
- Scheisse
- qsec
Um eine Ridge-Regression durchzuführen, verwenden wir Funktionen aus dem glmnet- Paket. Dieses Paket erfordert, dass die Antwortvariable ein Vektor ist und dass der Satz von Prädiktorvariablen der Klasse data.matrix angehört.
Der folgende Code zeigt, wie wir unsere Daten definieren:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
Schritt 2: Passen Sie das Ridge-Regressionsmodell an
Als nächstes verwenden wir die Funktion glmnet() , um das Ridge-Regressionsmodell anzupassen und alpha=0 anzugeben.
Beachten Sie, dass die Einstellung von Alpha auf 1 der Verwendung der Lasso-Regression und die Einstellung von Alpha auf einen Wert zwischen 0 und 1 der Verwendung eines elastischen Netzes entspricht.
Beachten Sie außerdem, dass die Ridge-Regression eine Standardisierung der Daten erfordert, sodass jede Prädiktorvariable einen Mittelwert von 0 und eine Standardabweichung von 1 aufweist.
Glücklicherweise übernimmt glmnet() diese Standardisierung automatisch für Sie. Wenn Sie die Variablen bereits standardisiert haben, können Sie standardize=False angeben.
library (glmnet)
#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )
#view summary of model
summary(model)
Length Class Mode
a0 100 -none- numeric
beta 400 dgCMatrix S4
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call
nobs 1 -none- numeric
Schritt 3: Wählen Sie einen optimalen Wert für Lambda
Als Nächstes ermitteln wir mithilfe der k-fachen Kreuzvalidierung den Lambda-Wert, der den niedrigsten mittleren quadratischen Testfehler (MSE) erzeugt.
Glücklicherweise verfügt glmnet über die Funktion cv.glmnet() , die automatisch eine k-fache Kreuzvalidierung mit k = 10 Mal durchführt.
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda
[1] 10.04567
#produce plot of test MSE by lambda value
plot(cv_model)
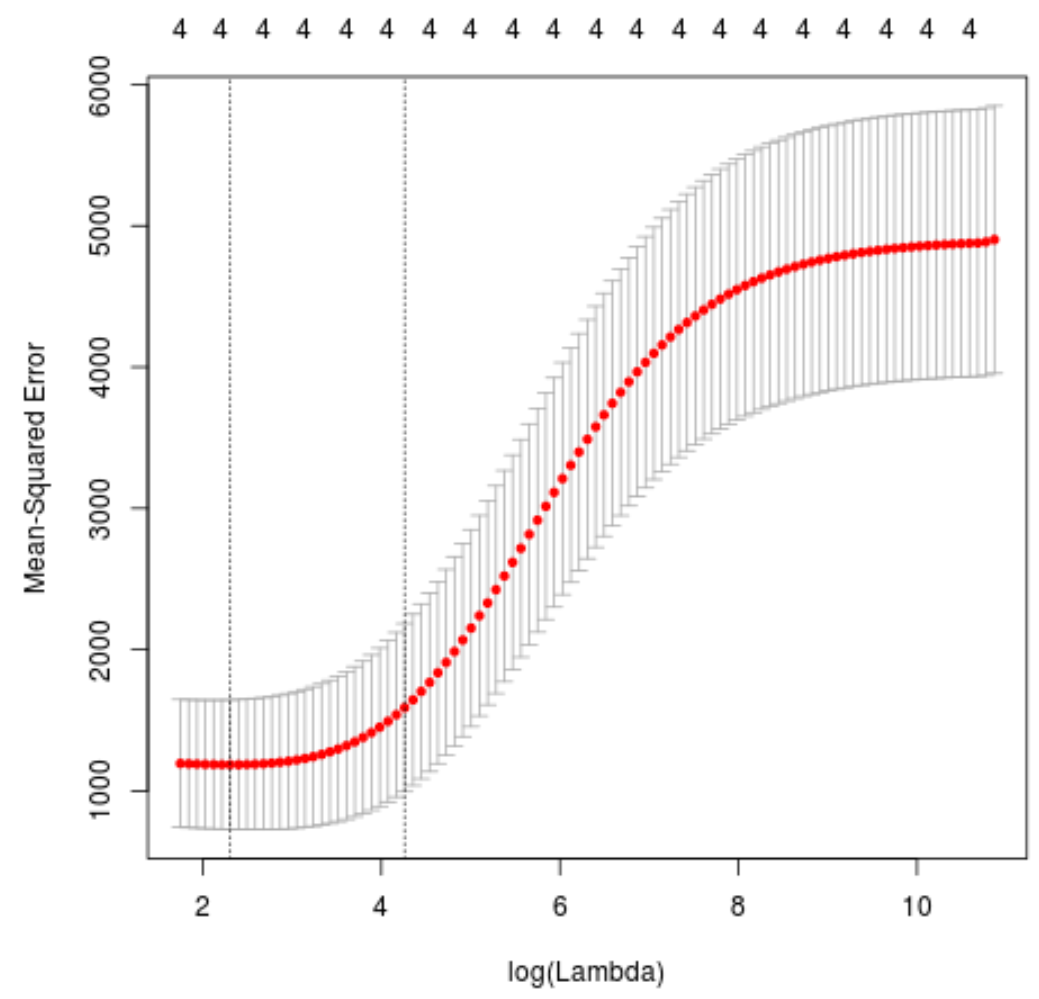
Der Lambda-Wert, der den MSE-Test minimiert, beträgt 10,04567 .
Schritt 4: Analysieren Sie das endgültige Modell
Schließlich können wir das endgültige Modell analysieren, das durch den optimalen Lambda-Wert erzeugt wird.
Wir können den folgenden Code verwenden, um die Koeffizientenschätzungen für dieses Modell zu erhalten:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721
Wir können auch ein Trace-Diagramm erstellen, um zu visualisieren, wie sich die Koeffizientenschätzungen aufgrund des Anstiegs von Lambda geändert haben:
#produce Ridge trace plot
plot(model, xvar = " lambda ")
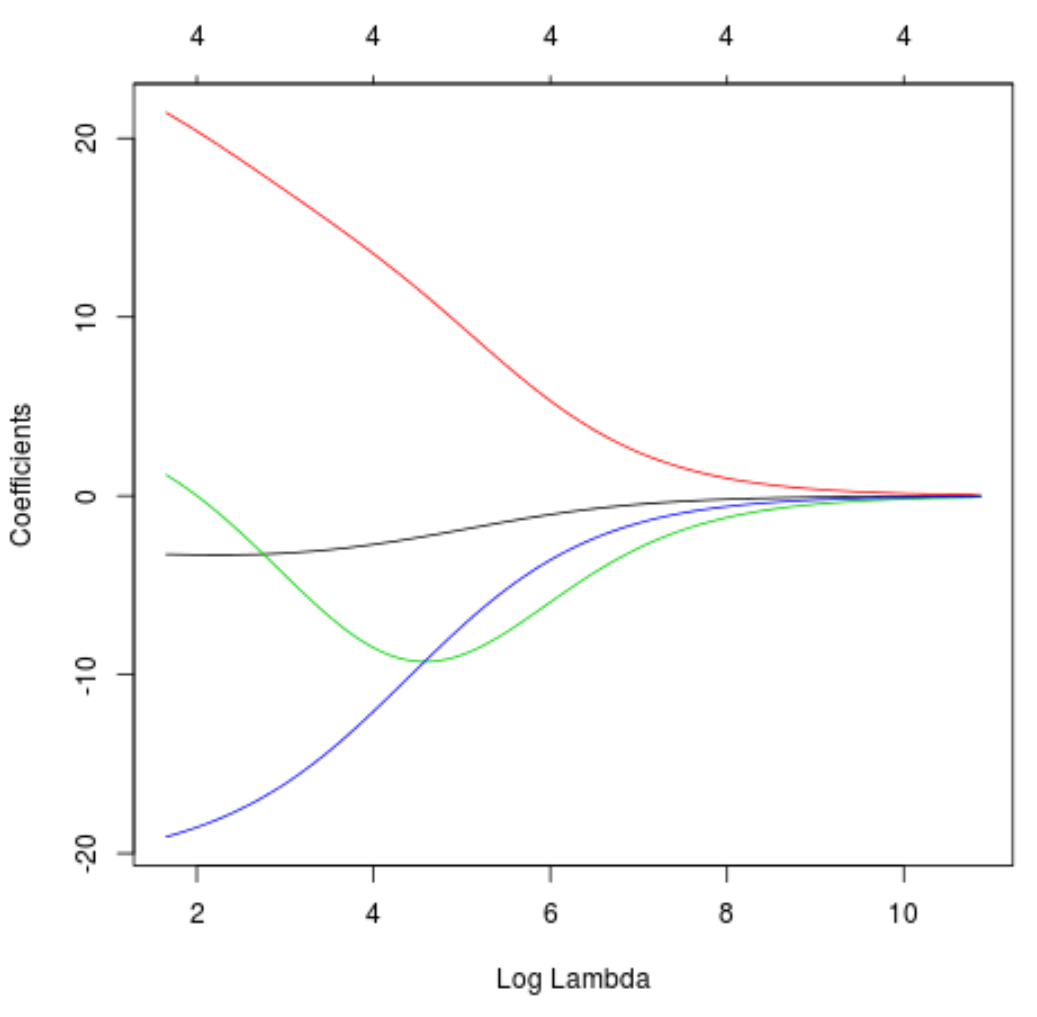
Schließlich können wir dasR-Quadrat des Modells anhand der Trainingsdaten berechnen:
#use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)
#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.7999513
Es stellt sich heraus, dass das R-Quadrat 0,7999513 beträgt. Das heißt, das beste Modell konnte 79,99 % der Variation der Antwortwerte der Trainingsdaten erklären.
Den vollständigen R-Code, der in diesem Beispiel verwendet wird, finden Sie hier .