Eine einführung in die polynomregression

Wenn wir einen Datensatz mit einer Prädiktorvariablen und einer Antwortvariablen haben, verwenden wir häufigeine einfache lineare Regression, um die Beziehung zwischen den beiden Variablen zu quantifizieren.

Bei der einfachen linearen Regression (SLR) wird jedoch davon ausgegangen, dass die Beziehung zwischen dem Prädiktor und der Antwortvariablen linear ist. In mathematischer Notation geschrieben geht SLR davon aus, dass die Beziehung die Form annimmt:

Y = β ₀ + β ₁ X + ε

In der Praxis kann die Beziehung zwischen den beiden Variablen jedoch tatsächlich nichtlinear sein, und der Versuch, eine lineare Regression zu verwenden, kann zu einem schlecht passenden Modell führen.

Eine Möglichkeit, eine nichtlineare Beziehung zwischen dem Prädiktor und der Antwortvariablen zu berücksichtigen, ist die Verwendung einer polynomialen Regression , die folgende Form annimmt:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

In dieser Gleichung wird h als Grad des Polynoms bezeichnet.

Wenn wir den Wert von h erhöhen, kann das Modell nichtlineare Beziehungen besser berücksichtigen. In der Praxis wählen wir jedoch selten, dass h größer als 3 oder 4 ist. Ab diesem Punkt wird das Modell zu flexibel und passt sich den Daten zu sehr an.

Technische Hinweise

• Obwohl die polynomielle Regression nichtlineare Daten anpassen kann, wird sie immer noch als eine Form der linearen Regression angesehen, da sie in den Koeffizienten _β1 , _β2 , …, _βh linear ist.
• Die polynomielle Regression kann auch für mehrere Prädiktorvariablen verwendet werden, allerdings entstehen dadurch Interaktionsterme im Modell, die das Modell bei Verwendung mehrerer Prädiktorvariablen äußerst komplex machen können.

Wann sollte die polynomielle Regression verwendet werden?

Wir verwenden die polynomielle Regression, wenn die Beziehung zwischen einem Prädiktor und einer Antwortvariablen nichtlinear ist.

Es gibt drei gängige Methoden zum Erkennen einer nichtlinearen Beziehung:

1. Erstellen Sie ein Streudiagramm.

Der einfachste Weg, eine nichtlineare Beziehung zu erkennen, besteht darin, ein Streudiagramm der Antwortvariablen gegenüber der Prädiktorvariablen zu erstellen.

Wenn wir beispielsweise das folgende Streudiagramm erstellen, können wir sehen, dass die Beziehung zwischen den beiden Variablen annähernd linear ist, sodass eine einfache lineare Regression für diese Daten wahrscheinlich gut funktionieren würde.

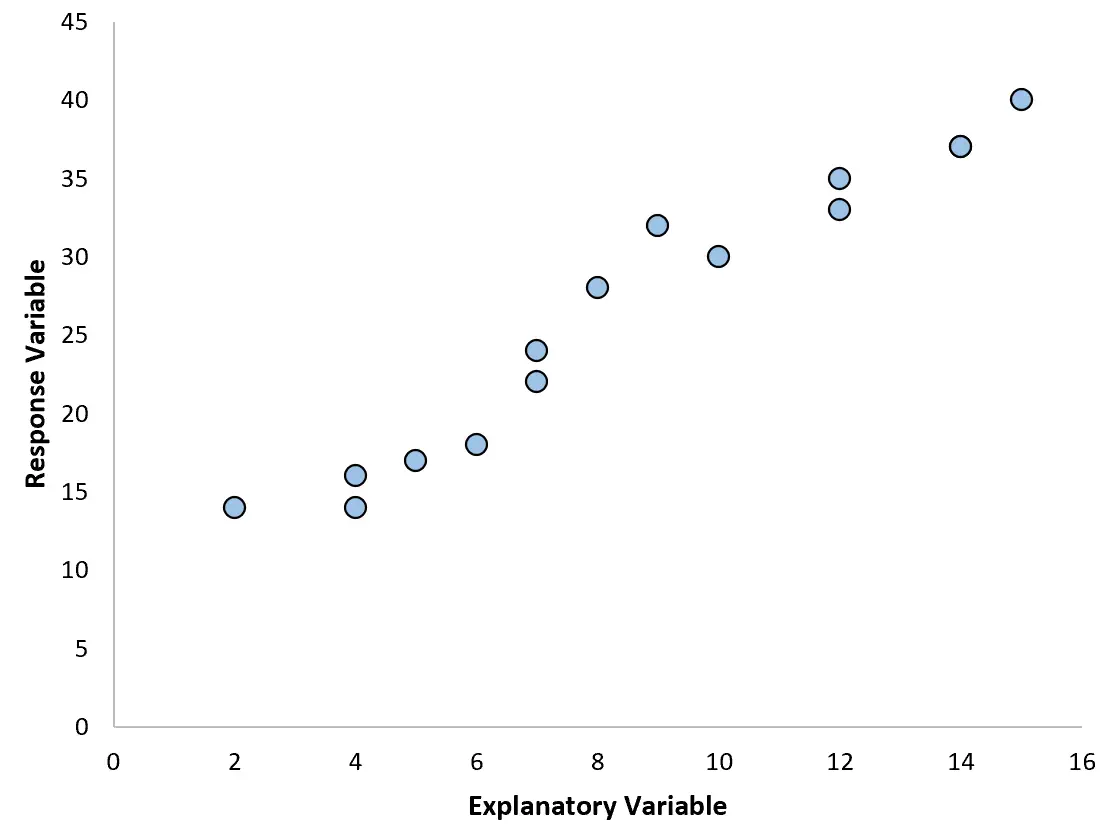
Wenn unser Streudiagramm jedoch wie eines der folgenden Diagramme aussieht, sehen wir möglicherweise, dass die Beziehung nichtlinear ist und daher eine polynomielle Regression eine gute Idee wäre:

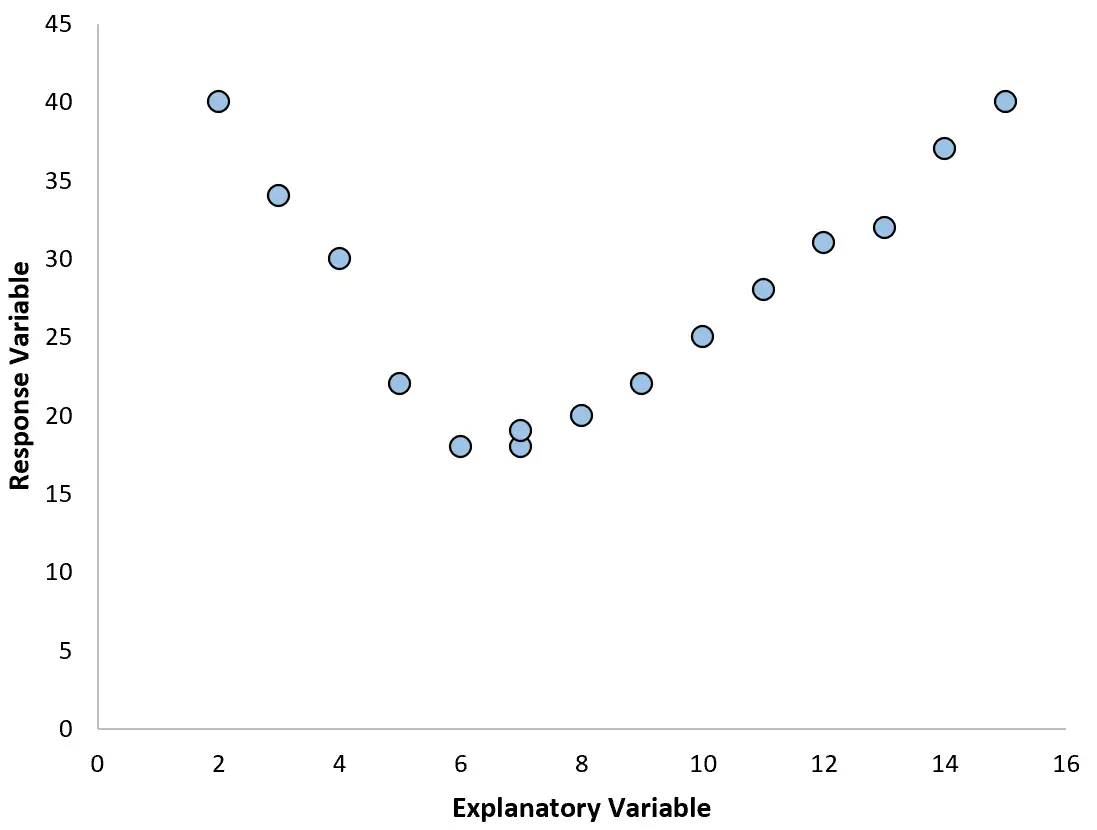
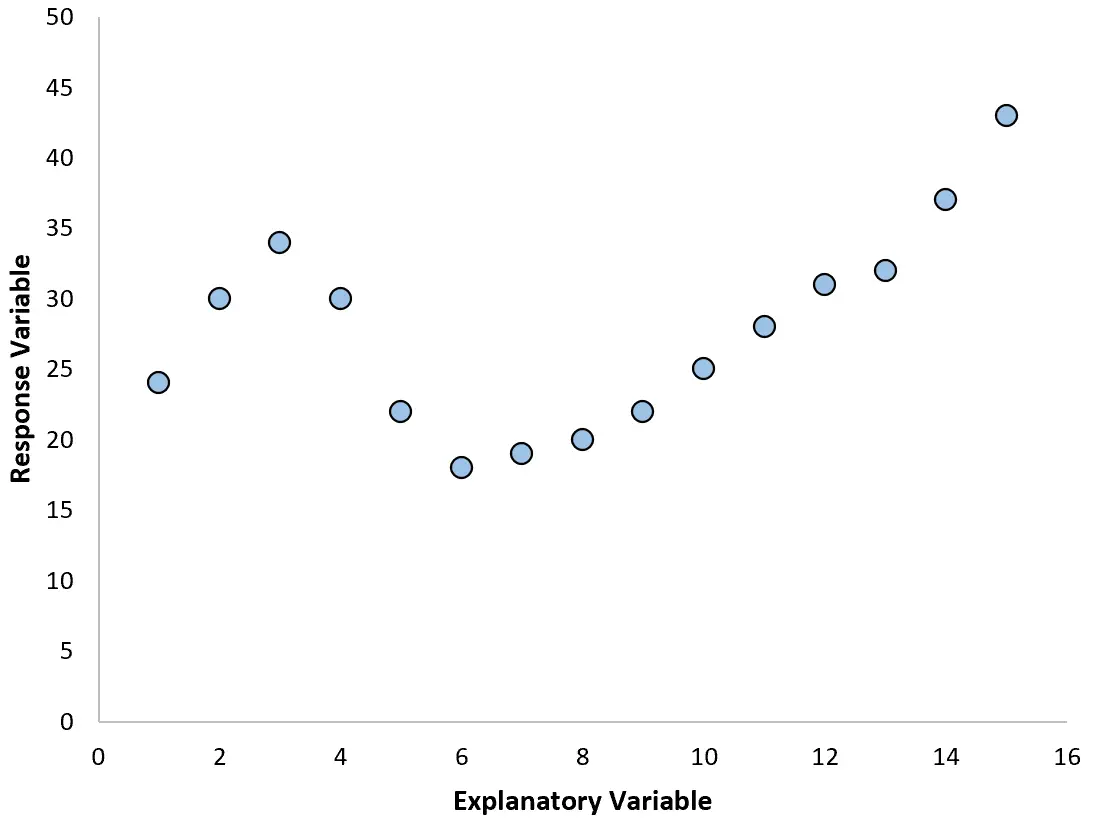
2. Erstellen Sie ein Diagramm der Residuen gegenüber dem angepassten Diagramm.

Eine andere Möglichkeit, Nichtlinearität zu erkennen, besteht darin, ein einfaches lineares Regressionsmodell an die Daten anzupassen und dann ein Diagramm der Residuen gegenüber den angepassten Werten zu erstellen.

Wenn die Plotresiduen annähernd gleichmäßig um Null herum verteilt sind und kein klarer Trend erkennbar ist, ist wahrscheinlich eine einfache lineare Regression ausreichend.

Wenn die Residuen im Diagramm jedoch einen nichtlinearen Trend zeigen, deutet dies darauf hin, dass die Beziehung zwischen dem Prädiktor und der Antwort wahrscheinlich nichtlinear ist.

3. Berechnen Sie das R ² des Modells.

Der R ² -Wert eines Regressionsmodells gibt an, wie viel Prozent der Variation in der Antwortvariablen durch die Prädiktorvariablen erklärt werden können.

Wenn Sie ein einfaches lineares Regressionsmodell an einen Datensatz anpassen und der R ² -Wert des Modells recht niedrig ist, könnte dies darauf hindeuten, dass die Beziehung zwischen dem Prädiktor und der Antwortvariablen komplexer ist als eine einfache lineare Beziehung.

Dies könnte ein Zeichen dafür sein, dass Sie stattdessen möglicherweise eine polynomielle Regression ausprobieren müssen.

Verwandt:Was ist ein guter R-Quadrat-Wert?

So wählen Sie den Grad des Polynoms

Ein polynomiales Regressionsmodell hat die folgende Form:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

In dieser Gleichung ist h der Grad des Polynoms.

Aber wie wählt man einen Wert für h ?

In der Praxis passen wir mehrere verschiedene Modelle mit unterschiedlichen h -Werten an und führen eine k-fache Kreuzvalidierung durch, um zu bestimmen, welches Modell den niedrigsten mittleren quadratischen Testfehler (MSE) erzeugt.

Beispielsweise können wir die folgenden Modelle an einen bestimmten Datensatz anpassen:

• Y = β ₀ + β ₁
• Y = β ₀ + β ₁ X + β ₂ X ²
• ^{Y =} _β0 + _β1X + _β2X2 + _β3X3
• Y = β ₀ + β ₁ X + β ₂ X ² + β ₃ X ³ + β ₄ X ⁴

Anschließend können wir die k-fache Kreuzvalidierung verwenden, um den MSE-Test für jedes Modell zu berechnen, der uns sagt, wie gut jedes Modell mit Daten abschneidet, die es noch nie zuvor gesehen hat.

Der Bias-Varianz-Kompromiss der polynomialen Regression

Bei der Verwendung der polynomialen Regression gibt es einen Kompromiss zwischen Bias und Varianz . Wenn wir den Grad des Polynoms erhöhen, nimmt die Verzerrung ab (da das Modell flexibler wird), aber die Varianz nimmt zu.

Wie bei allen Modellen des maschinellen Lernens müssen wir einen optimalen Kompromiss zwischen Bias und Varianz finden.

In den meisten Fällen kann dadurch der Grad des Polynoms bis zu einem gewissen Grad erhöht werden. Ab einem bestimmten Wert beginnt das Modell jedoch, sich an das Rauschen in den Daten anzupassen, und der MSE des Tests beginnt zu sinken.

Um sicherzustellen, dass wir ein Modell anpassen, das flexibel, aber nicht zu flexibel ist, verwenden wir eine k-fache Kreuzvalidierung, um das Modell zu finden, das den niedrigsten MSE-Test liefert.

So führen Sie eine polynomielle Regression durch

Die folgenden Tutorials bieten Beispiele für die Durchführung einer Polynomregression in unterschiedlicher Software:

So führen Sie eine Polynomregression in Excel durch
So führen Sie eine Polynomregression in R durch
So führen Sie eine Polynomregression in Python durch