Multivariate adaptive regressions-splines in r

Multivariate adaptive Regressionssplines (MARS) können verwendet werden, um nichtlineare Beziehungen zwischen einer Reihe von Prädiktorvariablen und einer Antwortvariablen zu modellieren.

Diese Methode funktioniert wie folgt:

1. Teilen Sie einen Datensatz in k Teile.

2. Passen Sie jedem Teil ein Regressionsmodell an.

3. Verwenden Sie die k-fache Kreuzvalidierung, um einen Wert für k auszuwählen.

Dieses Tutorial bietet ein schrittweises Beispiel für die Anpassung eines MARS-Modells an einen Datensatz in R.

Schritt 1: Laden Sie die erforderlichen Pakete

Für dieses Beispiel verwenden wir den ISLR- Lohndatensatz .   Paket, das die Jahresgehälter von 3.000 Personen zusammen mit einer Vielzahl von Prädiktorvariablen wie Alter, Bildung, Rasse und mehr enthält.

Bevor wir ein MARS-Modell an die Daten anpassen, laden wir die erforderlichen Pakete:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

Schritt 2: Daten anzeigen

Als Nächstes zeigen wir die ersten sechs Zeilen des Datensatzes an, mit dem wir arbeiten:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

Schritt 3: Erstellen und optimieren Sie das MARS-Modell

Als Nächstes erstellen wir das MARS-Modell für diesen Datensatz und führen eine k-fache Kreuzvalidierung durch, um zu bestimmen, welches Modell den niedrigsten Test-RMSE (mittlerer quadratischer Fehler) erzeugt.

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

Aus den Ergebnissen können wir ersehen, dass das Modell, das den niedrigsten Test-MSE erzeugte, ein Modell mit ausschließlich Effekten erster Ordnung (d. h. ohne Interaktionsterme) und 12 Termen war. Dieses Modell ergab einen quadratischen Mittelfehler (RMSE) von 33,8164 .

Hinweis: Wir haben method=“earth“ verwendet, um ein MARS-Modell anzugeben. Die Dokumentation zu dieser Methode finden Sie hier .

Wir können auch ein Diagramm erstellen, um den RMSE-Test basierend auf Grad und Anzahl der Begriffe zu visualisieren:

 #display test RMSE by terms and degree
ggplot(cv_mars)

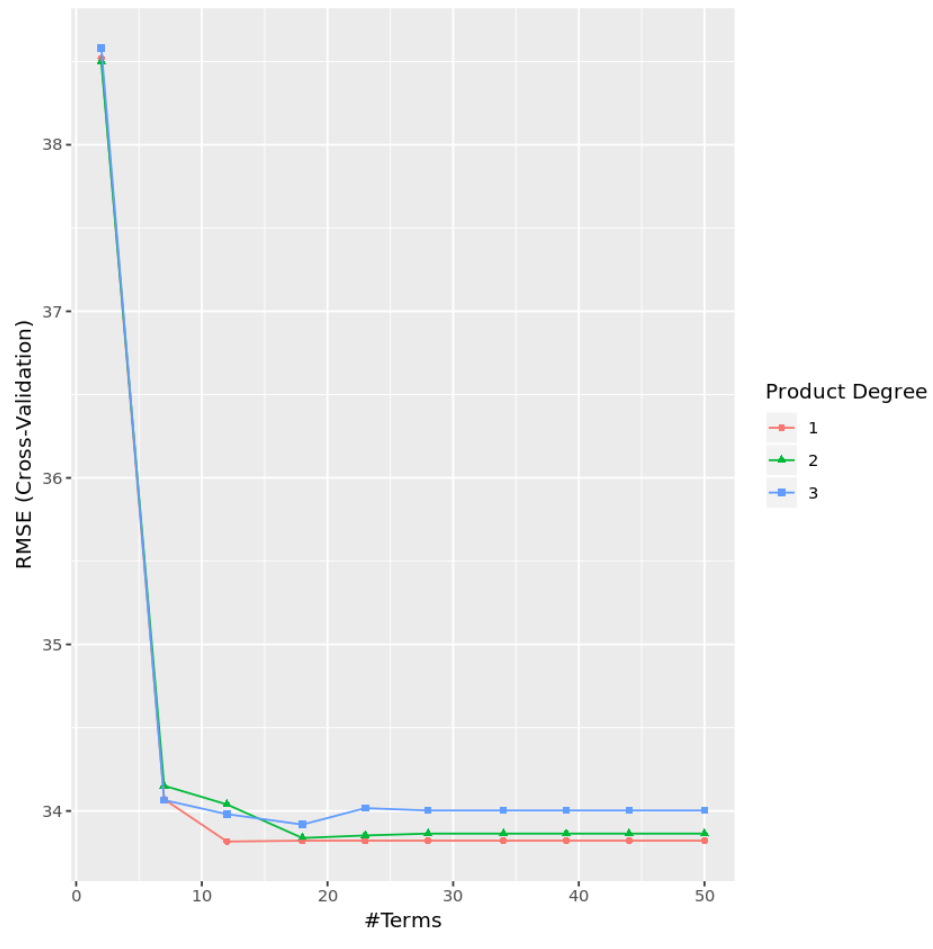
In der Praxis würden wir ein MARS-Modell mit mehreren anderen Modelltypen anpassen, wie zum Beispiel:

• Multiple lineare Regression
• Polynomielle Regression
• Peak-Regression
• Lasso-Regression
• Hauptkomponenten-Regression
• Teilweise kleinste Quadrate

Anschließend würden wir jedes Modell vergleichen, um zu bestimmen, welches zum geringsten Testfehler führt, und dieses Modell als das optimale zu verwendende Modell auswählen.

Den vollständigen R-Code, der in diesem Beispiel verwendet wird, finden Sie hier .