K-means-clustering in r: schritt-für-schritt-beispiel

Clustering ist eine Technik des maschinellen Lernens, die versucht, Gruppen von Beobachtungen innerhalb eines Datensatzes zu finden.

Das Ziel besteht darin, Cluster zu finden, bei denen die Beobachtungen innerhalb jedes Clusters einander recht ähnlich sind, während sich die Beobachtungen in verschiedenen Clustern deutlich voneinander unterscheiden.

Clustering ist eine Form des unbeaufsichtigten Lernens, da wir lediglich versuchen, die Struktur innerhalb eines Datensatzes zu finden, anstatt den Wert einer Antwortvariablen vorherzusagen.

Clustering wird häufig im Marketing eingesetzt, wenn Unternehmen Zugriff auf Informationen haben wie:

• Haushaltseinkommen
• Größe des Haushalts
• Leiter des Haushaltsberufs
• Entfernung zum nächstgelegenen Stadtgebiet

Wenn diese Informationen verfügbar sind, kann Clustering verwendet werden, um Haushalte zu identifizieren, die ähnlich sind und möglicherweise eher bestimmte Produkte kaufen oder besser auf eine bestimmte Art von Werbung reagieren.

Eine der häufigsten Formen des Clusterings ist das sogenannte K-Means-Clustering .

Was ist K-Means-Clustering?

K-Means-Clustering ist eine Technik, bei der wir jede Beobachtung aus einem Datensatz in einem von K Clustern platzieren.

Das Endziel besteht darin, K- Cluster zu haben, in denen die Beobachtungen innerhalb jedes Clusters einander ziemlich ähnlich sind, während sich die Beobachtungen in verschiedenen Clustern deutlich voneinander unterscheiden.

In der Praxis verwenden wir die folgenden Schritte, um K-Means-Clustering durchzuführen:

1. Wählen Sie einen Wert für K.

• Zunächst müssen wir entscheiden, wie viele Cluster wir in den Daten identifizieren möchten. Oft müssen wir einfach mehrere verschiedene Werte für K testen und die Ergebnisse analysieren, um zu sehen, welche Anzahl von Clustern für ein bestimmtes Problem am sinnvollsten erscheint.

2. Ordnen Sie jede Beobachtung zufällig einem Anfangscluster von 1 bis K zu.

3. Führen Sie das folgende Verfahren aus, bis sich die Clusterzuweisungen nicht mehr ändern.

• Berechnen Sie für jeden der K- Cluster den Schwerpunkt des Clusters. Dies ist einfach der Vektor der p- Mittelwert-Merkmale für die Beobachtungen des k-ten Clusters.
• Ordnen Sie jede Beobachtung dem Cluster mit dem nächstgelegenen Schwerpunkt zu. Hier wird der Abstand mithilfe des euklidischen Abstands definiert.

K-Means-Clustering in R

Das folgende Tutorial bietet ein schrittweises Beispiel für die Durchführung von K-Means-Clustering in R.

Schritt 1: Laden Sie die erforderlichen Pakete

Zuerst laden wir zwei Pakete, die mehrere nützliche Funktionen für das K-Means-Clustering in R enthalten.

 library (factoextra)
library (cluster)

Schritt 2: Daten laden und vorbereiten

Für dieses Beispiel verwenden wir den in R integrierten Datensatz „USArrests “, der die Anzahl der Festnahmen pro 100.000 Einwohner in jedem US-Bundesstaat im Jahr 1973 wegen Mordes , Körperverletzung und Vergewaltigung sowie den Prozentsatz der Stadtbevölkerung jedes Bundesstaates enthält Bereiche. , UrbanPop .

Der folgende Code zeigt, wie Sie Folgendes tun:

• Laden Sie den USArrests- Datensatz
• Entfernen Sie alle Zeilen mit fehlenden Werten
• Skalieren Sie jede Variable im Datensatz so, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 hat

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Schritt 3: Finden Sie die optimale Anzahl an Clustern

Um k-means-Clustering in R durchzuführen, können wir die integrierte Funktion kmeans() verwenden, die die folgende Syntax verwendet:

kmeans (Daten, Zentren, nstart)

Gold:

• data: Name des Datensatzes.
• Zentren: Die Anzahl der Cluster, bezeichnet mit k .
• nstart: die Anzahl der Erstkonfigurationen. Da es möglich ist, dass unterschiedliche anfängliche Startcluster zu unterschiedlichen Ergebnissen führen, wird empfohlen, mehrere unterschiedliche anfängliche Konfigurationen zu verwenden. Der k-means-Algorithmus findet die Anfangskonfigurationen, die zur kleinsten Variation innerhalb des Clusters führen.

Da wir nicht im Voraus wissen, wie viele Cluster optimal sind, erstellen wir zwei verschiedene Diagramme, die uns bei der Entscheidung helfen können:

1. Anzahl der Cluster im Verhältnis zur Gesamtsumme in Quadratsumme

Zuerst verwenden wir die Funktion fviz_nbclust() , um ein Diagramm der Anzahl der Cluster im Vergleich zur Gesamtsumme der Quadrate zu erstellen:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

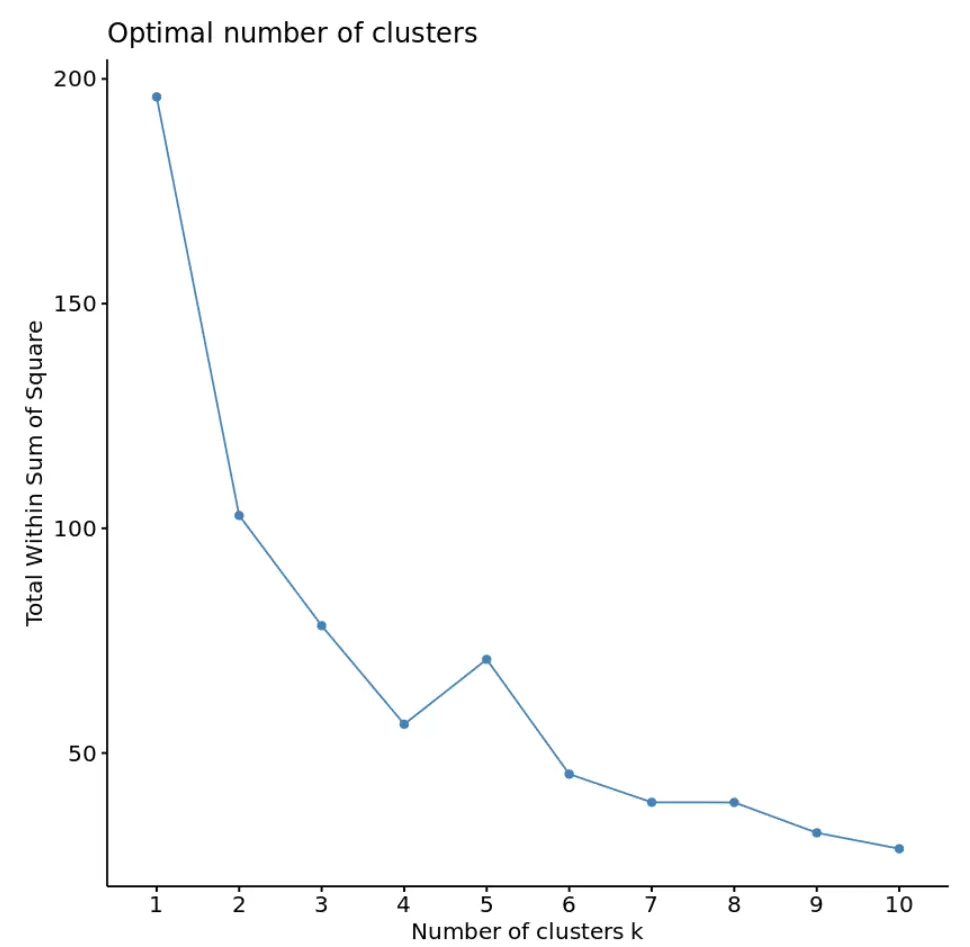
Wenn wir diese Art von Diagramm erstellen, suchen wir normalerweise nach einem „Knie“, an dem die Summe der Quadrate beginnt, sich zu „biegen“ oder einzuebnen. Dies ist im Allgemeinen die optimale Anzahl von Clustern.

Für dieses Diagramm scheint es, dass es bei k = 4 Clustern einen kleinen Knick oder eine „Krümmung“ gibt.

2. Anzahl der Cluster im Vergleich zur Lückenstatistik

Eine andere Möglichkeit, die optimale Anzahl von Clustern zu bestimmen, besteht darin, eine Metrik namens Abweichungsstatistik zu verwenden, die die gesamte Variation innerhalb des Clusters für verschiedene Werte von k mit ihren erwarteten Werten für eine Verteilung ohne Clustering vergleicht.

Wir können die Lückenstatistik für jede Anzahl von Clustern mit der Funktion clusGap() aus dem Clusterpaket berechnen und die Cluster mit der Lückenstatistik mit der Funktion fviz_gap_stat() grafisch darstellen:

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

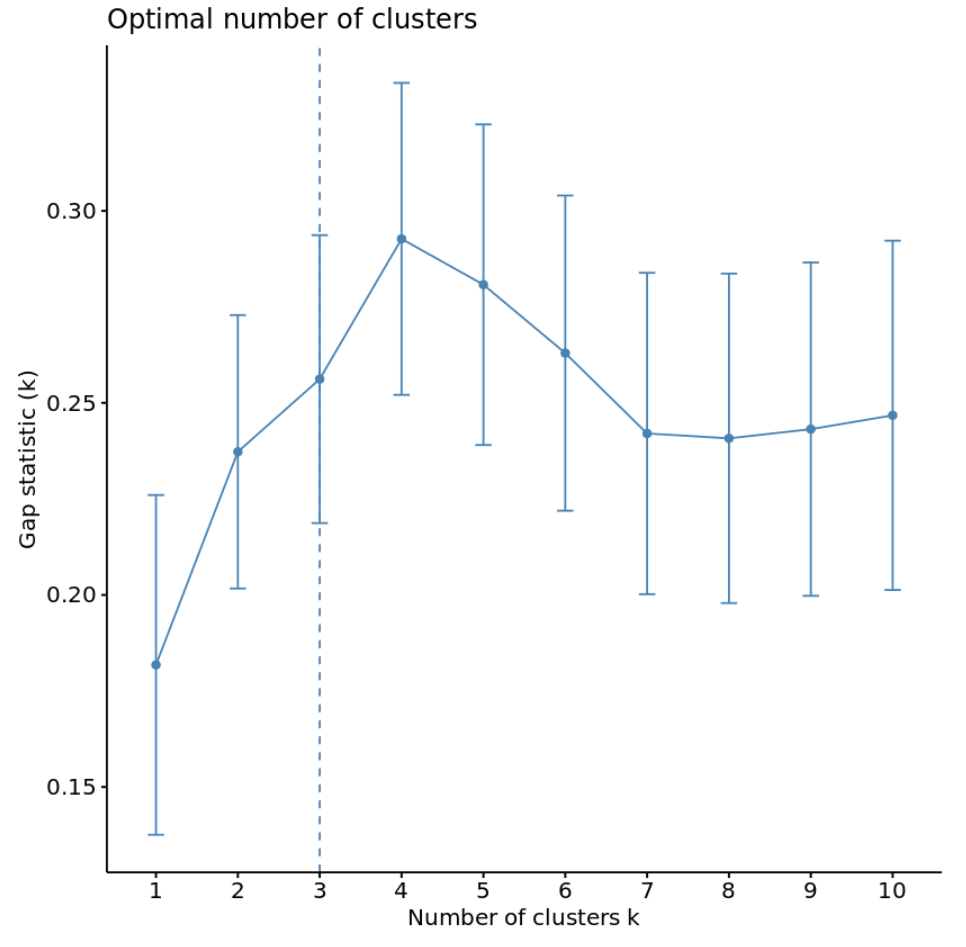
Aus der Grafik können wir ersehen, dass die Lückenstatistik bei k = 4 Clustern am höchsten ist, was der Ellbogenmethode entspricht, die wir zuvor verwendet haben.

Schritt 4: Führen Sie K-Means-Clustering mit optimalem K durch

Schließlich können wir ein k-Means-Clustering für den Datensatz durchführen, indem wir den optimalen Wert für k von 4 verwenden:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Anhand der Ergebnisse können wir Folgendes erkennen:

• Dem ersten Cluster wurden 16 Staaten zugeordnet
• Dem zweiten Cluster sind 13 Staaten zugeordnet
• Dem dritten Cluster wurden 13 Staaten zugeordnet
• Dem vierten Cluster wurden 8 Staaten zugeordnet

Mit der Funktion fivz_cluster() können wir die Cluster in einem Streudiagramm visualisieren, das die ersten beiden Hauptkomponenten auf den Achsen anzeigt:

 #plot results of final k-means model
fviz_cluster(km, data = df)

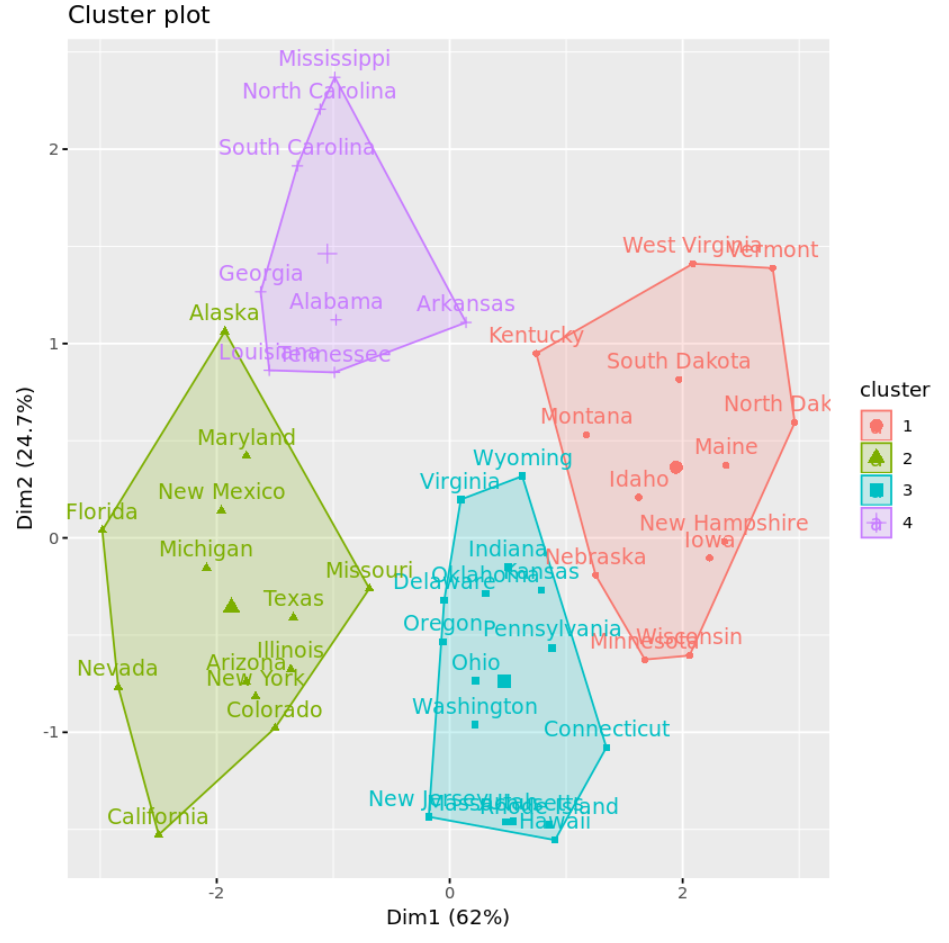
Wir können auch die Funktion Aggregate() verwenden, um den Durchschnitt der Variablen in jedem Cluster zu ermitteln:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

Wir interpretieren diese Ausgabe wie folgt:

• Die durchschnittliche Zahl der Morde pro 100.000 Einwohner in den Staaten der Gruppe 1 beträgt 3,6 .
• Die durchschnittliche Zahl der Übergriffe pro 100.000 Bürger beträgt in den Staaten der Gruppe 1 78,5 .
• Der durchschnittliche Prozentsatz der Einwohner, die in einem städtischen Gebiet in den Staaten der Gruppe 1 leben, beträgt 52,1 % .
• Die durchschnittliche Zahl der Vergewaltigungen pro 100.000 Bürger beträgt in den Staaten der Gruppe 1 12,2 .

Und so weiter.

Wir können auch die Clusterzuordnungen jedes Staates zum Originaldatensatz hinzufügen:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Vor- und Nachteile von K-Means-Clustering

K-Means-Clustering bietet die folgenden Vorteile:

• Es ist ein schneller Algorithmus.
• Es kann große Datenmengen gut verarbeiten.

Es hat jedoch die folgenden potenziellen Nachteile:

• Dies erfordert, dass wir die Anzahl der Cluster angeben, bevor wir den Algorithmus ausführen.
• Es reagiert empfindlich auf Ausreißer.

Zwei Alternativen zum K-Means-Clustering sind das K-Means-Clustering und das hierarchische Clustering.

Den vollständigen R-Code, der in diesem Beispiel verwendet wird, finden Sie hier .