K-medoide in r: schritt-für-schritt-beispiel

Clustering ist eine Technik des maschinellen Lernens, die versucht, Gruppen oder Cluster von Beobachtungen innerhalb eines Datensatzes zu finden.

Das Ziel besteht darin, Cluster zu finden, bei denen die Beobachtungen innerhalb jedes Clusters einander recht ähnlich sind, während sich die Beobachtungen in verschiedenen Clustern deutlich voneinander unterscheiden.

Clustering ist eine Form des unbeaufsichtigten Lernens, da wir lediglich versuchen, die Struktur innerhalb eines Datensatzes zu finden, anstatt den Wert einer Antwortvariablen vorherzusagen.

Clustering wird häufig im Marketing eingesetzt, wenn Unternehmen Zugriff auf Informationen haben wie:

• Haushaltseinkommen
• Größe des Haushalts
• Leiter des Haushaltsberufs
• Entfernung zum nächstgelegenen Stadtgebiet

Wenn diese Informationen verfügbar sind, kann Clustering verwendet werden, um Haushalte zu identifizieren, die ähnlich sind und möglicherweise eher bestimmte Produkte kaufen oder besser auf eine bestimmte Art von Werbung reagieren.

Eine der häufigsten Formen des Clusterings ist das sogenannte K-Means-Clustering .

Leider kann diese Methode durch Ausreißer beeinflusst werden, weshalb eine häufig verwendete Alternative das k-Medoids-Clustering ist.

Was ist K-Medoids-Clustering?

Beim K-Medoid-Clustering handelt es sich um eine Technik, bei der wir jede Beobachtung in einem Datensatz einem von K- Clustern zuordnen.

Das Endziel besteht darin, K- Cluster zu haben, in denen die Beobachtungen innerhalb jedes Clusters einander ziemlich ähnlich sind, während sich die Beobachtungen in verschiedenen Clustern deutlich voneinander unterscheiden.

In der Praxis verwenden wir die folgenden Schritte, um K-Means-Clustering durchzuführen:

1. Wählen Sie einen Wert für K.

• Zunächst müssen wir entscheiden, wie viele Cluster wir in den Daten identifizieren möchten. Oft müssen wir einfach mehrere verschiedene Werte für K testen und die Ergebnisse analysieren, um zu sehen, welche Anzahl von Clustern für ein bestimmtes Problem am sinnvollsten erscheint.

2. Ordnen Sie jede Beobachtung zufällig einem Anfangscluster von 1 bis K zu.

3. Führen Sie das folgende Verfahren aus, bis sich die Clusterzuweisungen nicht mehr ändern.

• Berechnen Sie für jeden der K- Cluster den Schwerpunkt des Clusters. Dies ist der Vektor der p- Mediane der Merkmale für die Beobachtungen des k- ten Clusters.
• Ordnen Sie jede Beobachtung dem Cluster mit dem nächstgelegenen Schwerpunkt zu. Hier wird der Abstand mithilfe des euklidischen Abstands definiert.

Technischer Hinweis:

Da k-medoids Clusterschwerpunkte anhand von Medianen und nicht anhand von Mittelwerten berechnet, ist es tendenziell robuster gegenüber Ausreißern als k-means.

In der Praxis führen k-means und k-medoids zu ähnlichen Ergebnissen, wenn der Datensatz keine extremen Ausreißer enthält.

K-Medoide häufen sich in R

Das folgende Tutorial bietet ein schrittweises Beispiel für die Durchführung von K-Medoids-Clustering in R.

Schritt 1: Laden Sie die erforderlichen Pakete

Zuerst werden wir zwei Pakete laden, die mehrere nützliche Funktionen für das k-Medoid-Clustering in R enthalten.

 library (factoextra)
library (cluster)

Schritt 2: Daten laden und vorbereiten

Für dieses Beispiel verwenden wir den in R integrierten Datensatz „USArrests “, der die Anzahl der Festnahmen pro 100.000 Einwohner in jedem US-Bundesstaat im Jahr 1973 wegen Mordes , Körperverletzung und Vergewaltigung sowie den Prozentsatz der Stadtbevölkerung jedes Bundesstaates enthält Bereiche. , UrbanPop .

Der folgende Code zeigt, wie Sie Folgendes tun:

• Laden Sie den USArrests- Datensatz
• Entfernen Sie alle Zeilen mit fehlenden Werten
• Skalieren Sie jede Variable im Datensatz so, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 hat

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Schritt 3: Finden Sie die optimale Anzahl an Clustern

Um k-Medoid-Clustering in R durchzuführen, können wir die Funktion pam() verwenden, die für „Partitionierung um Mediane“ steht und die folgende Syntax verwendet:

pam(Daten, k, Metrik = „Euklidisch“, Stand = FALSCH)

Gold:

• data: Name des Datensatzes.
• k: Die Anzahl der Cluster.
• Metrik: Die Metrik, die zur Berechnung der Entfernung verwendet werden soll. Der Standardwert ist Euclidean , Sie können aber auch manhattan angeben.
• Stand: Ob jede Variable im Datensatz normalisiert werden soll oder nicht. Der Standardwert ist false.

Da wir nicht im Voraus wissen, welche Anzahl von Clustern optimal ist, erstellen wir zwei verschiedene Diagramme, die uns bei der Entscheidung helfen können:

1. Anzahl der Cluster im Verhältnis zur Gesamtsumme in Quadratsumme

Zuerst verwenden wir die Funktion fviz_nbclust() , um ein Diagramm der Anzahl der Cluster im Vergleich zur Gesamtsumme der Quadrate zu erstellen:

 fviz_nbclust(df, pam, method = “ wss ”) 

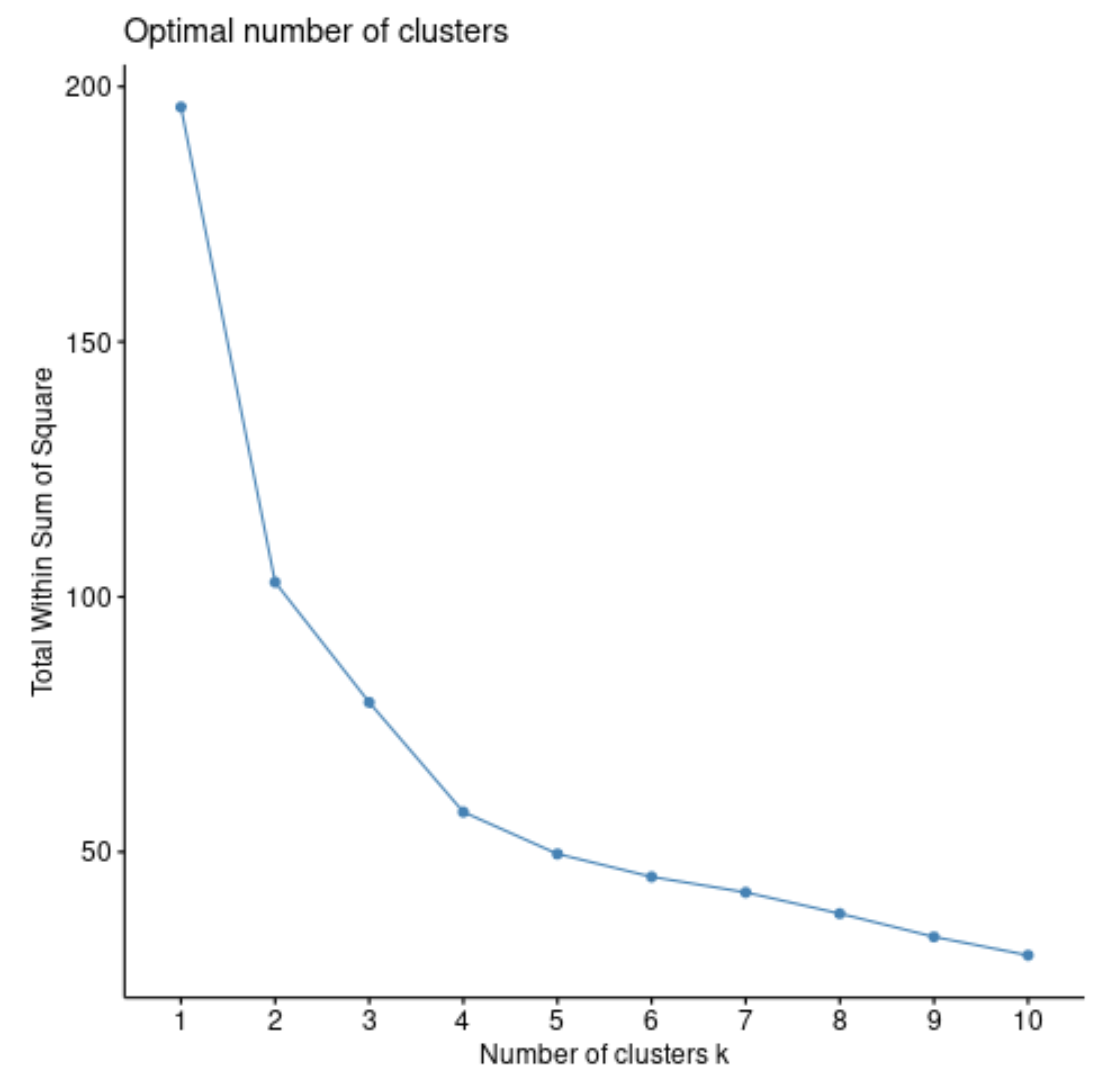
Die Gesamtsumme der Quadrate wird im Allgemeinen immer größer, wenn wir die Anzahl der Cluster erhöhen. Wenn wir diese Art von Diagramm erstellen, suchen wir nach einem „Knie“, an dem sich die Summe der Quadrate zu „verbiegen“ oder einzuebnen beginnt.

Der Krümmungspunkt des Diagramms entspricht im Allgemeinen der optimalen Anzahl von Clustern. Über diesen Wert hinaus ist eine Überanpassung wahrscheinlich.

Für dieses Diagramm scheint es, dass es bei k = 4 Clustern einen kleinen Knick oder eine „Krümmung“ gibt.

2. Anzahl der Cluster im Vergleich zur Lückenstatistik

Eine andere Möglichkeit, die optimale Anzahl von Clustern zu bestimmen, besteht darin, eine Metrik namens Abweichungsstatistik zu verwenden, die die gesamte Variation innerhalb des Clusters für verschiedene Werte von k mit ihren erwarteten Werten für eine Verteilung ohne Clustering vergleicht.

Wir können die Lückenstatistik für jede Anzahl von Clustern mit der Funktion clusGap() aus dem Clusterpaket berechnen sowie eine Darstellung der Cluster im Vergleich zur Lückenstatistik mit der Funktion fviz_gap_stat() erstellen:

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = pam,
                    K.max = 10, #max clusters to consider
                    B = 50) #total bootstrapped iterations

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

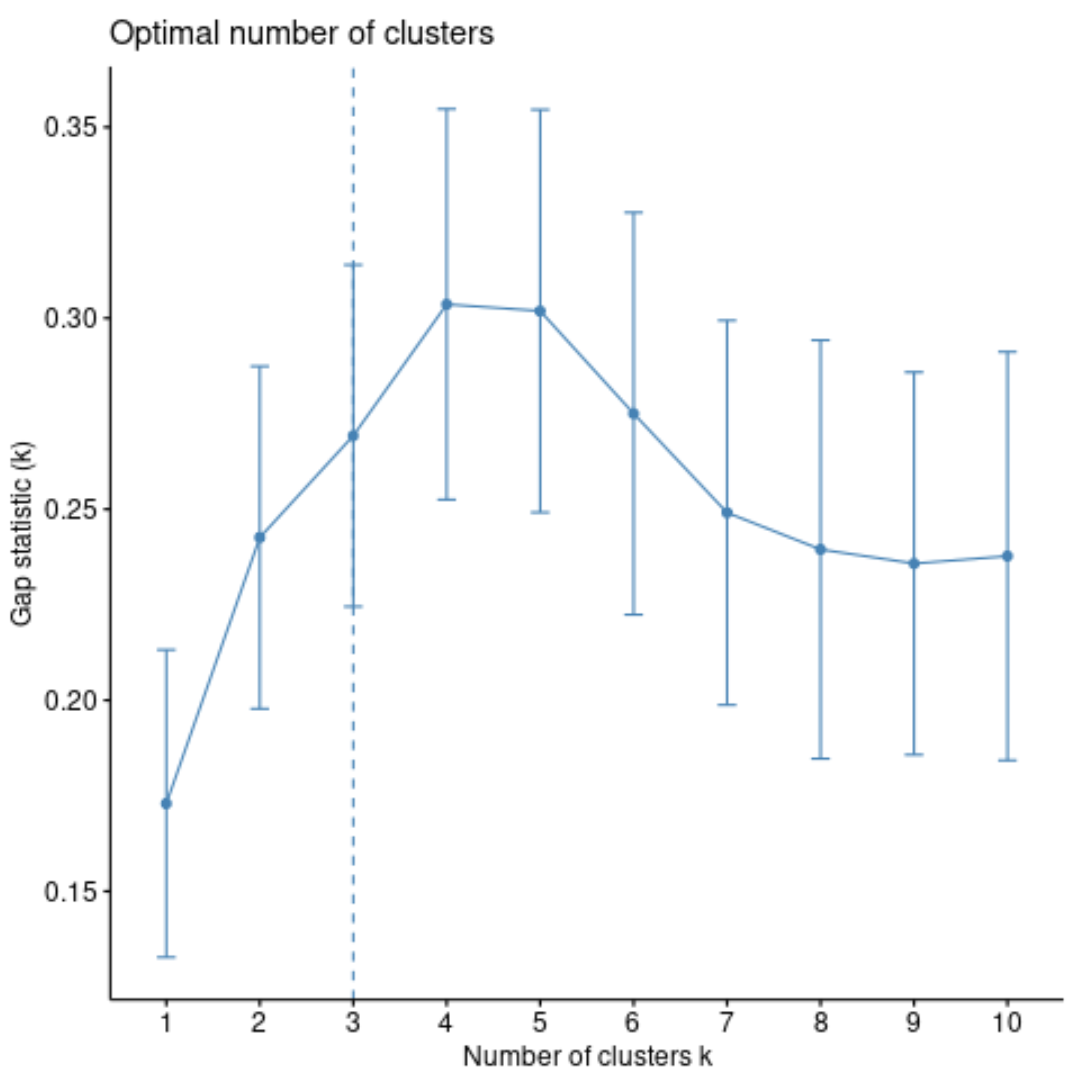
Aus der Grafik können wir ersehen, dass die Lückenstatistik bei k = 4 Clustern am höchsten ist, was der Ellbogenmethode entspricht, die wir zuvor verwendet haben.

Schritt 4: Führen Sie K-Medoids-Clustering mit Optimal K durch

Schließlich können wir k-Medoids-Clustering für den Datensatz durchführen und dabei den optimalen Wert für k von 4 verwenden:

 #make this example reproducible
set.seed(1)

#perform k-medoids clustering with k = 4 clusters
kmed <- pam(df, k = 4)

#view results
kmed

              ID Murder Assault UrbanPop Rape
Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473
Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993
Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211
New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
Vector clustering:
       Alabama Alaska Arizona Arkansas California 
             1 2 2 1 2 
      Colorado Connecticut Delaware Florida Georgia 
             2 3 3 2 1 
        Hawaii Idaho Illinois Indiana Iowa 
             3 4 2 3 4 
        Kansas Kentucky Louisiana Maine Maryland 
             3 3 1 4 2 
 Massachusetts Michigan Minnesota Mississippi Missouri 
             3 2 4 1 3 
       Montana Nebraska Nevada New Hampshire New Jersey 
             3 3 2 4 3 
    New Mexico New York North Carolina North Dakota Ohio 
             2 2 1 4 3 
      Oklahoma Oregon Pennsylvania Rhode Island South Carolina 
             3 3 3 3 1 
  South Dakota Tennessee Texas Utah Vermont 
             4 1 2 3 4 
      Virginia Washington West Virginia Wisconsin Wyoming 
             3 3 4 4 3 
Objective function:
   build swap 
1.035116 1.027102 

Available components:
 [1] "medoids" "id.med" "clustering" "objective" "isolation" 
 [6] "clusinfo" "silinfo" "diss" "call" "data"          

Beachten Sie, dass es sich bei allen vier Clusterschwerpunkten um tatsächliche Beobachtungen im Datensatz handelt. Oben in der Ausgabe können wir sehen, dass die vier Schwerpunkte die folgenden Zustände haben:

• Alabama
• Michigan
• Oklahoma
• New Hampshire

Mit der Funktion fivz_cluster() können wir die Cluster in einem Streudiagramm visualisieren, das die ersten beiden Hauptkomponenten auf den Achsen anzeigt:

 #plot results of final k-medoids model
fviz_cluster(kmed, data = df)

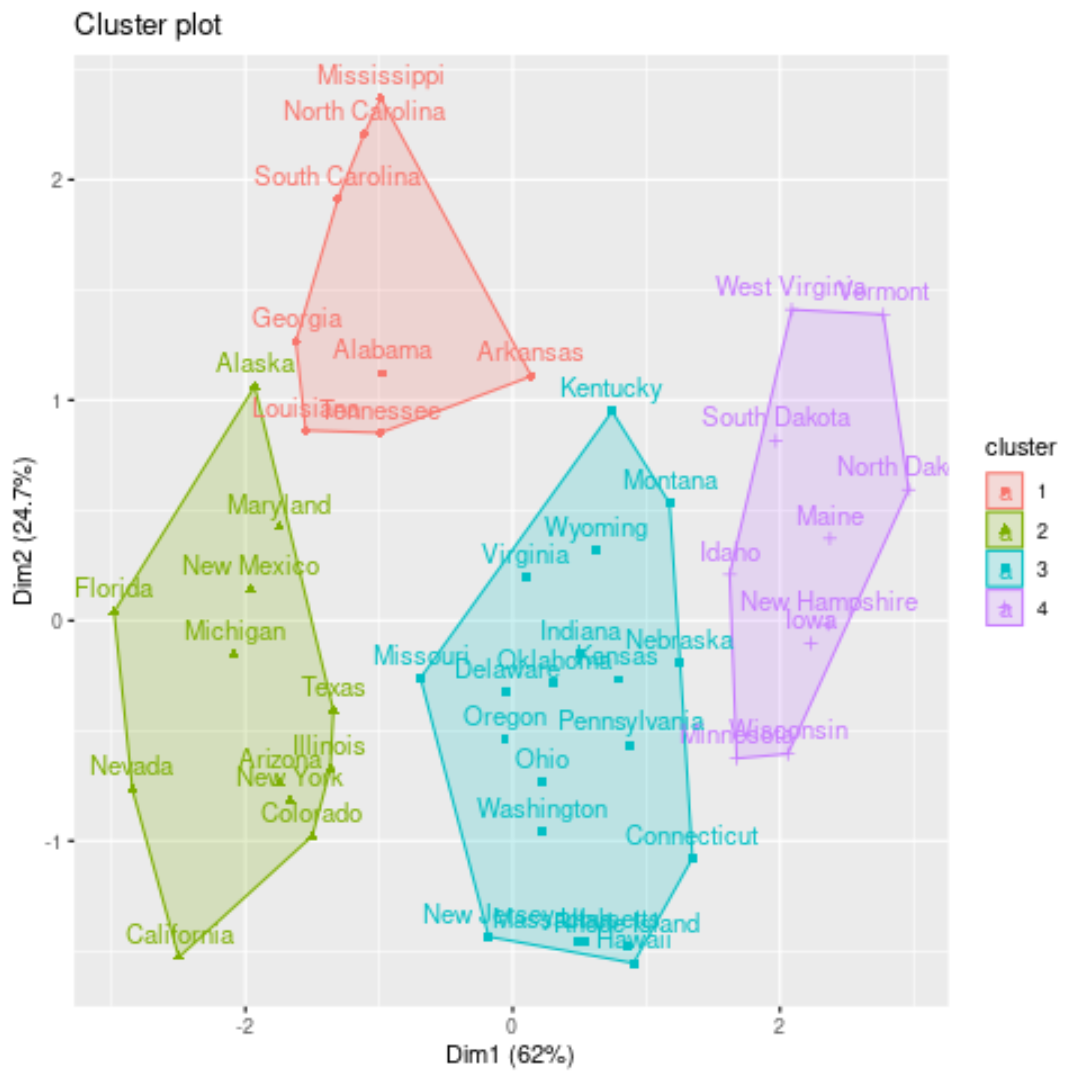
Wir können auch die Clusterzuordnungen jedes Staates zum Originaldatensatz hinzufügen:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = kmed$cluster)

#view final data
head(final_data)

           Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 1
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 1
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Den vollständigen R-Code, der in diesem Beispiel verwendet wird, finden Sie hier .