Arten von asymmetrie
In diesem Artikel erfahren Sie, wie viele Arten von Asymmetrien es in der Statistik gibt. So wird jede Art von Asymmetrie anhand von Beispielen erläutert und Sie können außerdem sehen, wie die Asymmetrie einer Verteilung berechnet wird.
Welche Arten von Asymmetrie gibt es?
In der Statistik gibt es drei Arten von Asymmetrie :
- Positive Schiefe : Die Verteilung weist rechts vom Mittelwert mehr unterschiedliche Werte auf als links.
- Negative Schiefe : Die Verteilung hat links vom Mittelwert mehr unterschiedliche Werte als rechts davon.
- Symmetrie : Die Verteilung hat links und rechts vom Mittelwert die gleiche Anzahl von Werten.
Jede Art von Asymmetrie wird im Folgenden ausführlicher erläutert.
positive Asymmetrie
Wenn eine Verteilung eine positive Schiefe aufweist, bedeutet dies, dass der rechte Rand ihres Diagramms länger ist als der linke Rand. Das heißt, die Verteilung weist rechts vom Mittelwert mehr unterschiedliche Werte auf.
Die Kurve im vorherigen Beispiel ist positiv asymmetrisch, da rechts vom Mittelwert viel mehr Werte liegen als links. Wie Sie dem Diagramm entnehmen können, ist der grün dargestellte Balken viel größer als der orangefarbene Balken.
negative Asymmetrie
In der Statistik spricht man von einer negativen Schiefe einer Verteilung, wenn der linke Rand ihres Diagramms länger ist als der rechte Rand. Das heißt, eine negativ verzerrte Verteilung bedeutet, dass sie links vom Mittelwert mehr unterschiedliche Werte aufweist.
Wenn Sie sich das vorherige Diagramm ansehen, gibt es links vom Mittelwert mehr Werte als rechts, sodass die Kurve negativ schief ist.
Symmetrie
Eine Verteilung ist symmetrisch , wenn die Anzahl der Werte links vom Mittelwert gleich der Anzahl der Werte rechts vom Mittelwert ist. Der Durchschnitt fungiert daher als Symmetrieachse.
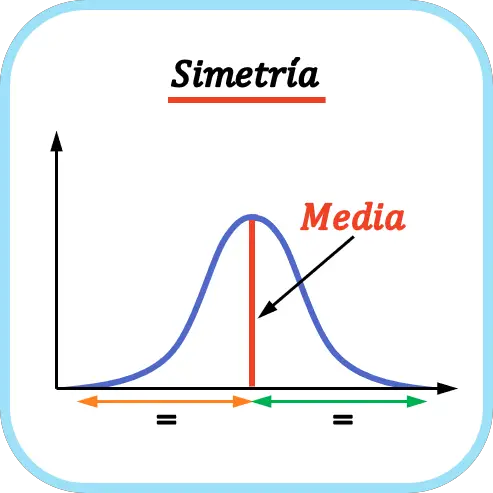
Wie im obigen Beispiel gezeigt, stimmt die Anzahl der Werte links vom Mittelwert der dargestellten Wahrscheinlichkeitsverteilung mit der Anzahl der Werte rechts vom Mittelwert überein, es handelt sich also um eine symmetrische Verteilung.
So bestimmen Sie die Art der Asymmetrie
Nachdem wir nun die verschiedenen Arten von Asymmetrien in der Statistik kennen, wollen wir uns nun ansehen, wie wir herausfinden können, welcher Art von Asymmetrie eine Wahrscheinlichkeitsverteilung entspricht.
Traditionell wird erklärt, dass wir die Art der Schiefe einer Verteilung anhand der Beziehung zwischen ihrem Mittelwert und ihrem Median (ob größer, äquivalent oder kleiner) erkennen können. Diese Eigenschaft ist jedoch nicht immer zufrieden. Um die Schiefe einer Verteilung zu bestimmen, muss daher der Fisher-Skewness-Koeffizient berechnet werden.
Der Fisher-Asymmetriekoeffizient wird nach folgender Formel berechnet:
![\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]](https://statorials.org/wp-content/ql-cache/quicklatex.com-a7c403ee0227e6c36f8c80eaeafba63e_l3.png "Rendered by QuickLaTeX.com")
Oder gleichwertig:
![\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}](https://statorials.org/wp-content/ql-cache/quicklatex.com-92f7c8482d520258f24cc0166d898d1e_l3.png "Rendered by QuickLaTeX.com")
Gold
ist die mathematische Erwartung ,
das arithmetische Mittel und
die Standardabweichung .
Und sobald der Fisher-Koeffizient berechnet wurde, ermöglicht sein Vorzeichen die Bestimmung, welche Art von Asymmetrie die Verteilung aufweist:
- Wenn der Schiefekoeffizient nach Fisher positiv ist, ist die Verteilung positiv schief.
- Wenn der Schiefekoeffizient nach Fisher negativ ist, ist die Verteilung negativ schief.
- Wenn die Verteilung symmetrisch ist, ist der Schiefekoeffizient nach Fisher gleich Null (das Gegenteil ist nicht immer der Fall).
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen