Symmetrische verteilung: definition + beispiele

In der Statistik spricht man von einer symmetrischen Verteilung, bei der sich die linke und rechte Seite spiegeln.

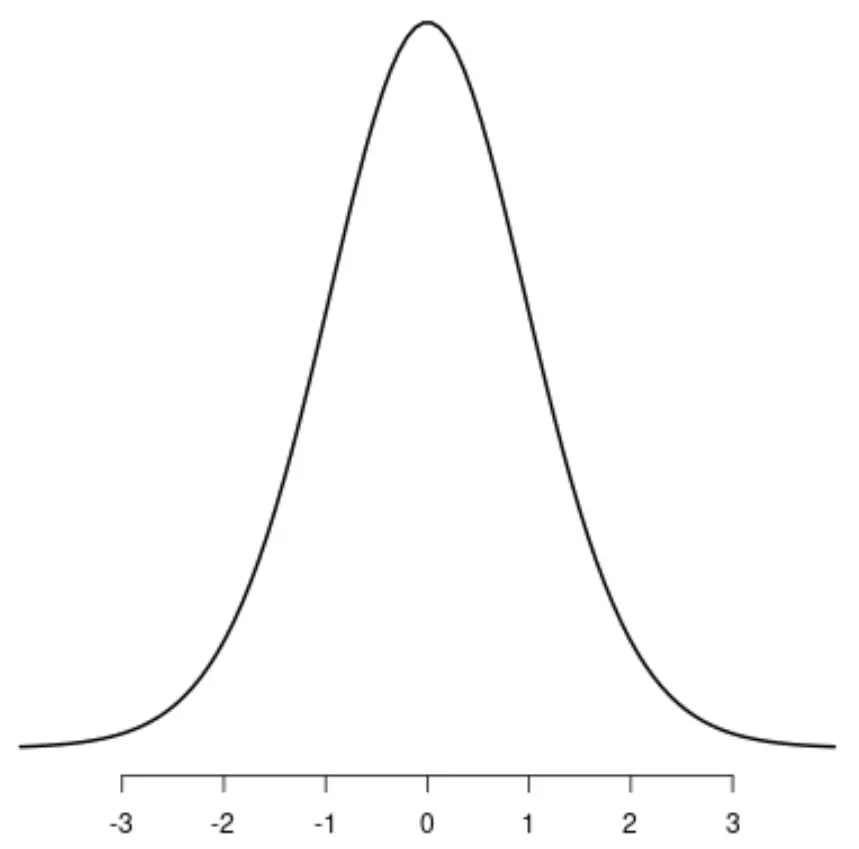
Die bekannteste symmetrische Verteilung ist die Normalverteilung , die eine ausgeprägte Glockenform aufweist.

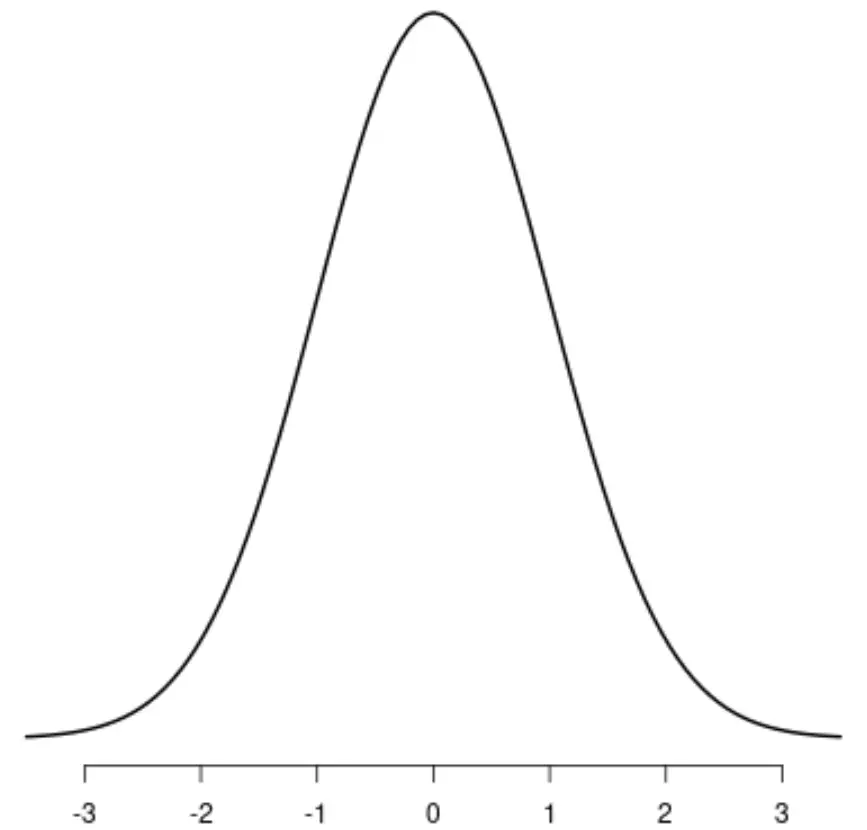
Wenn Sie eine Linie in der Mitte der Verteilung zeichnen würden, würden sich die linke und rechte Seite der Verteilung perfekt widerspiegeln:

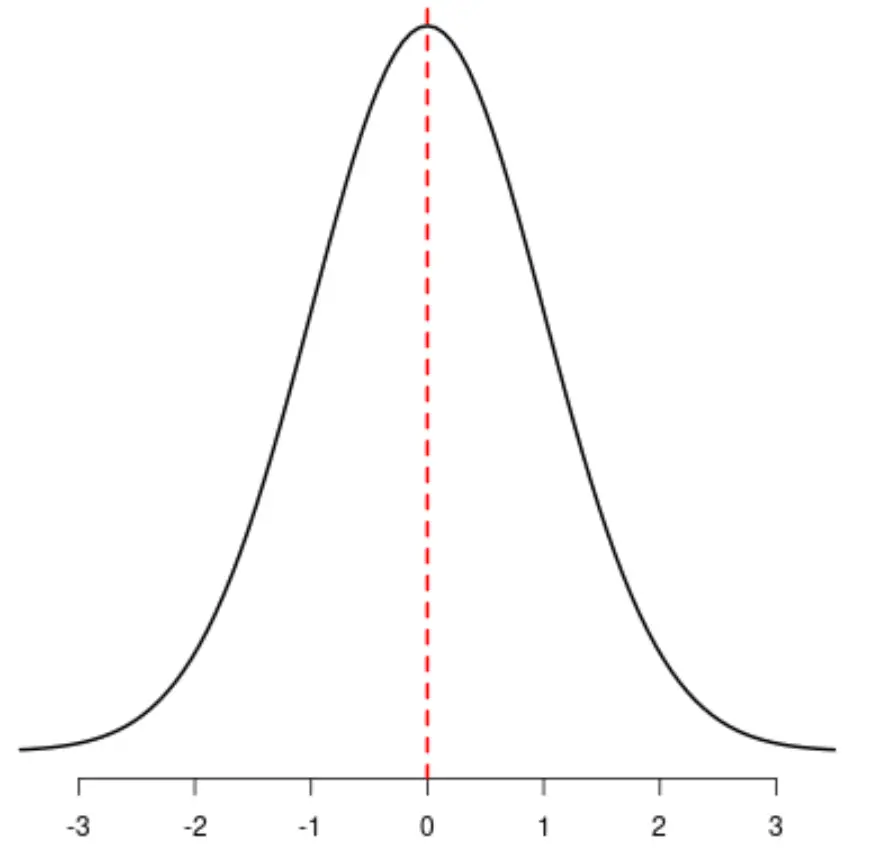
In der Statistik ist Schiefe eine Möglichkeit, die Symmetrie einer Verteilung zu beschreiben. Dieser Wert kann negativ, null oder positiv sein.

Bei symmetrischen Verteilungen ist die Asymmetrie Null.

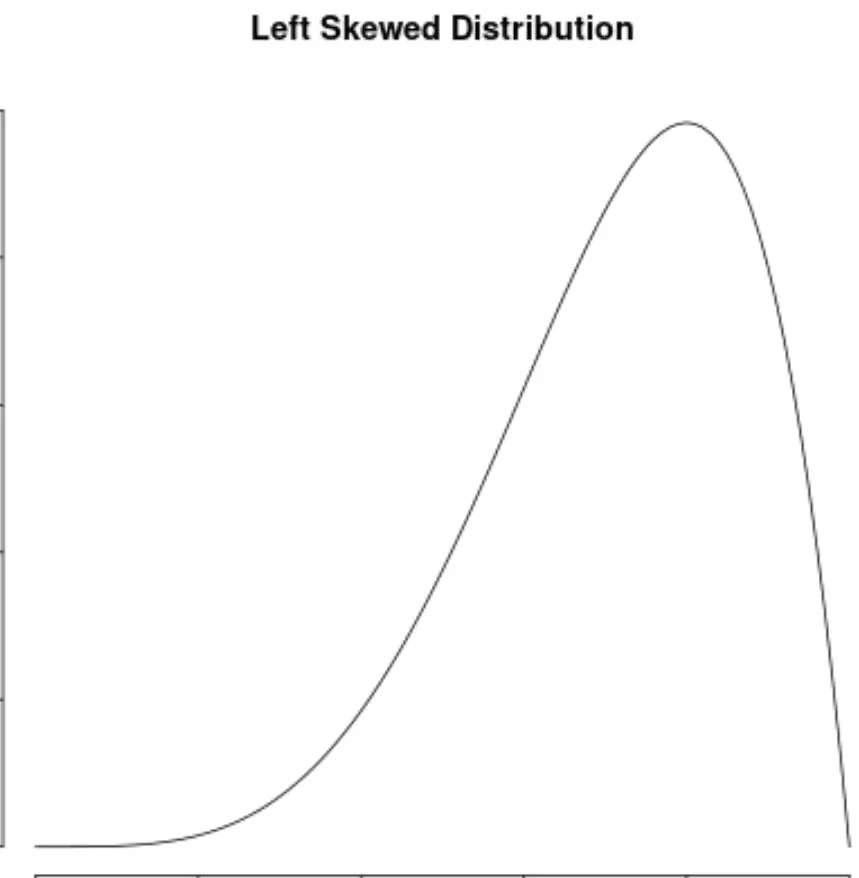
Dies steht im Gegensatz zu linksschiefen Verteilungen, die eine negative Schiefe aufweisen:

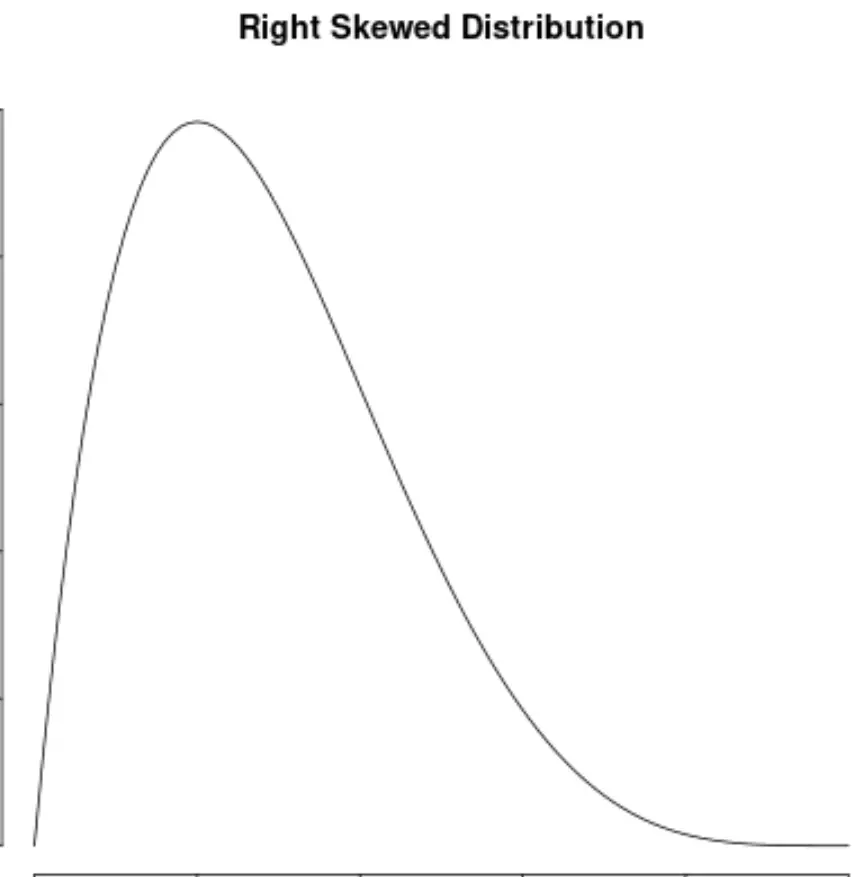
Dies steht auch im Gegensatz zu rechtsschiefen Verteilungen, die eine positive Schiefe aufweisen:

Eigenschaften symmetrischer Verteilungen

Bei einer symmetrischen Verteilung sind Mittelwert, Median und Modus alle gleich.

Denken Sie jeweils an die folgenden Definitionen:

• Durchschnitt: der Durchschnittswert.
• Median: der Durchschnittswert.
• Modus: der Wert, der am häufigsten erscheint.

Bei einer symmetrischen Verteilung ist jeder dieser Werte gleich dem anderen.

In jedem der bisherigen Beispiele haben wir unimodale Verteilungen als Beispiele verwendet – Verteilungen mit nur einem „Peak“. Eine Verteilung kann jedoch auch bimodal und symmetrisch sein.

Eine bimodale Verteilung ist eine Verteilung mit zwei Spitzen.

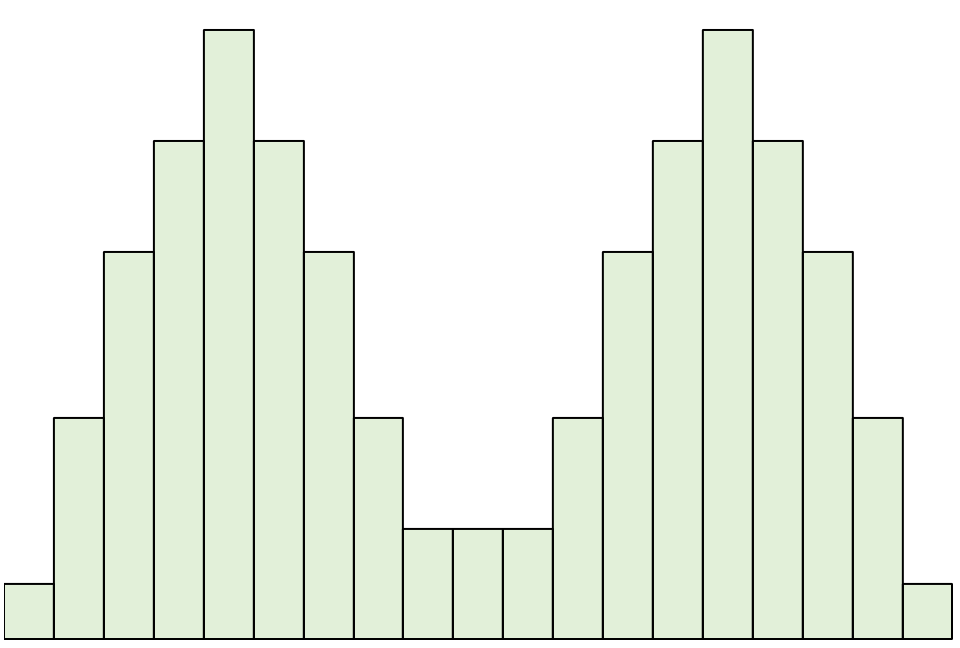
Beachten Sie, dass sich die linke und rechte Seite immer noch spiegeln, wenn wir eine Linie in der Mitte dieser Verteilung zeichnen.

Für diese Verteilungen sind Mittelwert und Median gleich. Der Modus liegt jedoch in beiden Eckpunkten.

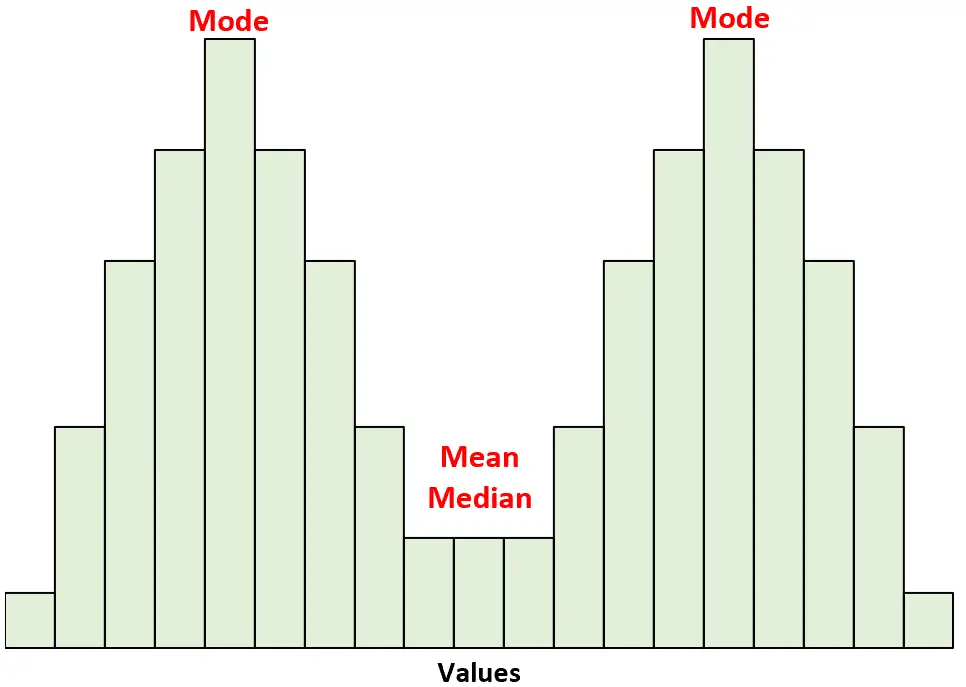
Weitere Beispiele für symmetrische Verteilungen

Neben der Normalverteilung sind auch folgende Verteilungen symmetrisch:

Die Verteilung t

Gleichmäßige Verteilung

Die Cauchy-Verteilung

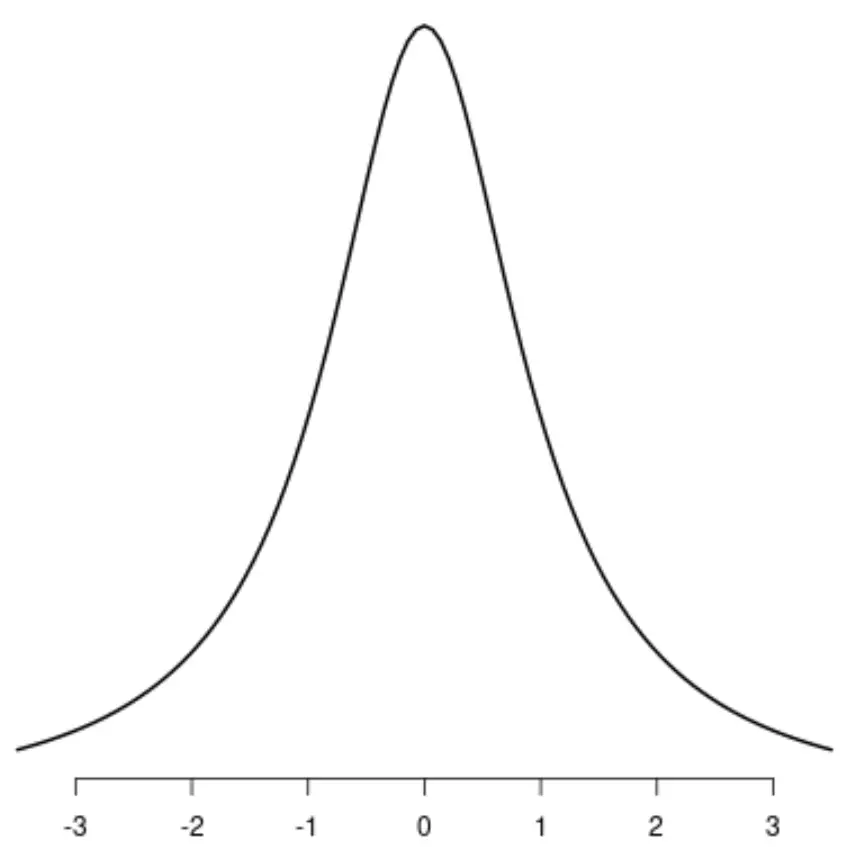
Wenn Sie eine Linie in der Mitte einer dieser Verteilungen zeichnen würden, würden sich die linke und rechte Seite jeder Verteilung perfekt widerspiegeln.

Symmetrische Verteilungen und der zentrale Grenzwertsatz

Einer der wichtigsten Sätze in der gesamten Statistik ist der zentrale Grenzwertsatz, der besagt, dass die Stichprobenverteilung eines Stichprobenmittelwerts annähernd normal ist, wenn die Stichprobengröße groß genug ist, auch wenn die Grundgesamtheitsverteilung nicht normal ist .

Um den zentralen Grenzwertsatz anwenden zu können, muss die Stichprobengröße groß genug sein. Es stellt sich heraus, dass die Frage, wie viele Menschen genau „groß genug“ sind, von der zugrunde liegenden Form der Bevölkerungsverteilung abhängt.

Besonders:

• Wenn die Bevölkerungsverteilung symmetrisch ist, reicht manchmal eine Stichprobengröße von nur 15 aus.
• Bei einer schiefen Bevölkerungsverteilung ist in der Regel eine Stichprobe von mindestens 30 Personen erforderlich.
• Wenn die Bevölkerungsverteilung extrem schief ist, kann eine Stichprobe von 40 oder mehr Personen erforderlich sein.

Der Vorteil symmetrischer Verteilungen besteht also darin, dass wir kleinere Stichprobengrößen benötigen, um den zentralen Grenzwertsatz bei der Berechnung von Konfidenzintervallen oder der Durchführung von Hypothesentests anzuwenden.

Zusätzliche Ressourcen

Eine Einführung in den zentralen Grenzwertsatz
Was ist eine bimodale Verteilung?
Ein Leitfaden für links- und rechtsschiefe Verteilungen