Was ist eine multimodale verteilung?

Eine multimodale Verteilung ist eine Wahrscheinlichkeitsverteilung mit zwei oder mehr Modi.

Wenn Sie ein Histogramm zur Visualisierung einer multimodalen Verteilung erstellen, werden Sie feststellen, dass diese mehrere Spitzen aufweist:

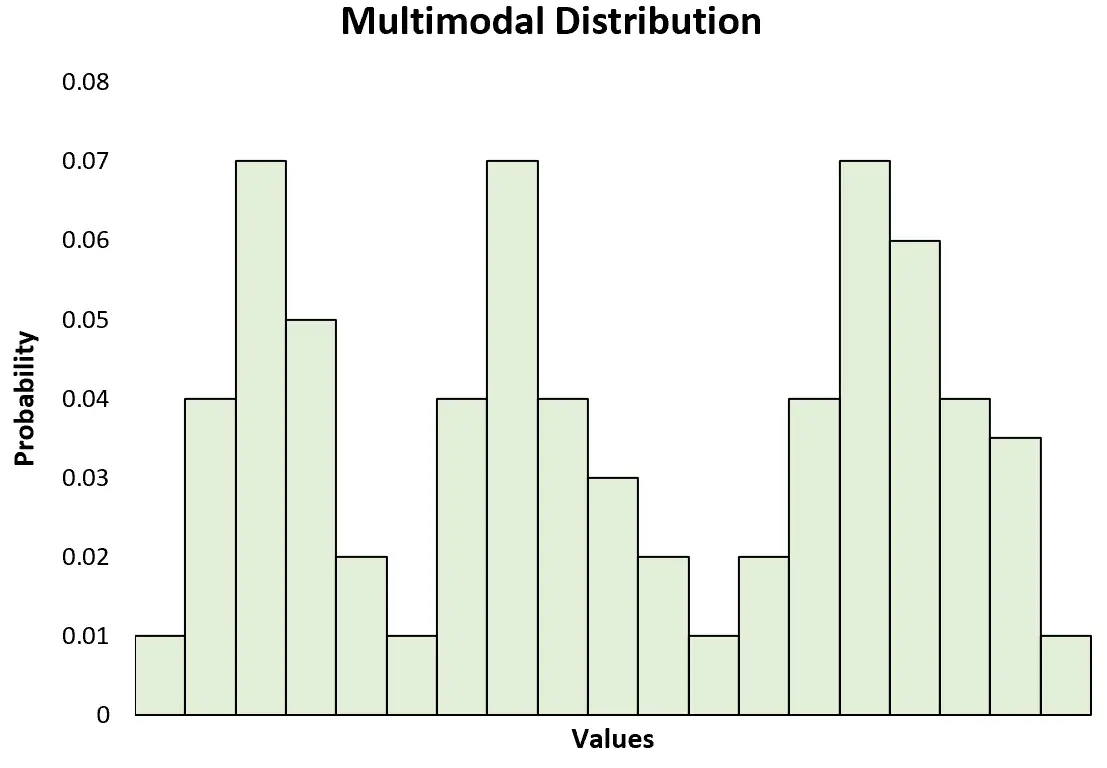
Wenn eine Verteilung genau zwei Spitzen aufweist, wird sie als bimodale Verteilung betrachtet, also eine spezielle Art multimodaler Verteilung.

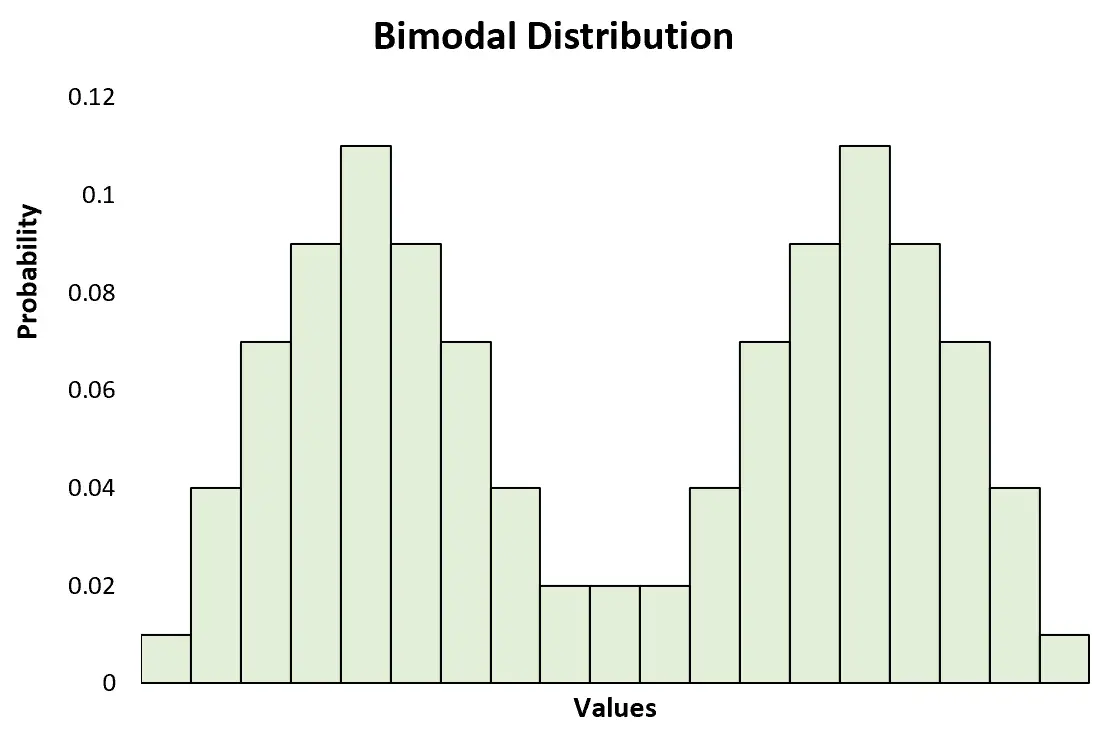
Dies steht im Gegensatz zu einer unimodalen Verteilung, die nur einen Peak aufweist:

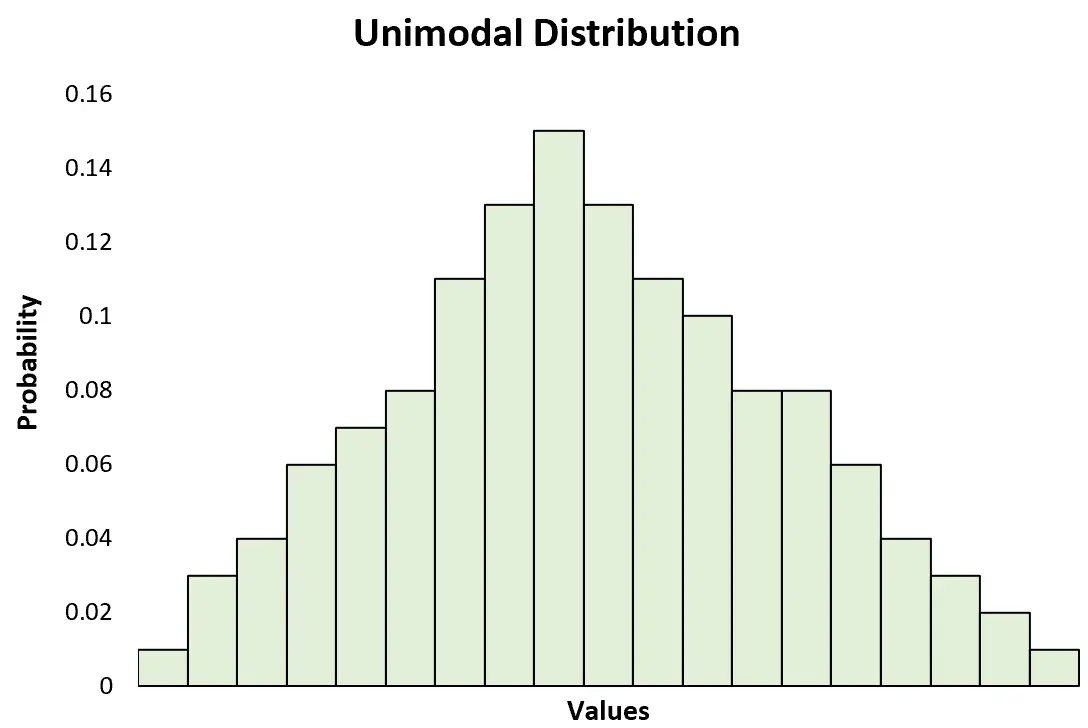
Obwohl unimodale Verteilungen wie die Normalverteilung am häufigsten zur Erklärung von Themen in der Statistik verwendet werden, kommen multimodale Verteilungen in der Praxis tatsächlich recht häufig vor, sodass es nützlich ist zu wissen, wie man sie erkennt und analysiert.

Beispiele für multimodale Verteilungen

Hier sind einige Beispiele für multimodale Verteilungen.

Beispiel 1: Verteilung der Prüfungsergebnisse

Angenommen, ein Professor gibt seiner Klasse eine Prüfung. Einige Schüler lernten, andere nicht. Wenn der Professor ein Histogramm der Prüfungsergebnisse erstellt, folgt es einer multimodalen Verteilung mit einer Spitze bei niedrigen Ergebnissen für Studenten, die nicht studiert haben, und einer weiteren Spitze bei hohen Ergebnissen für Studenten, die studiert haben:

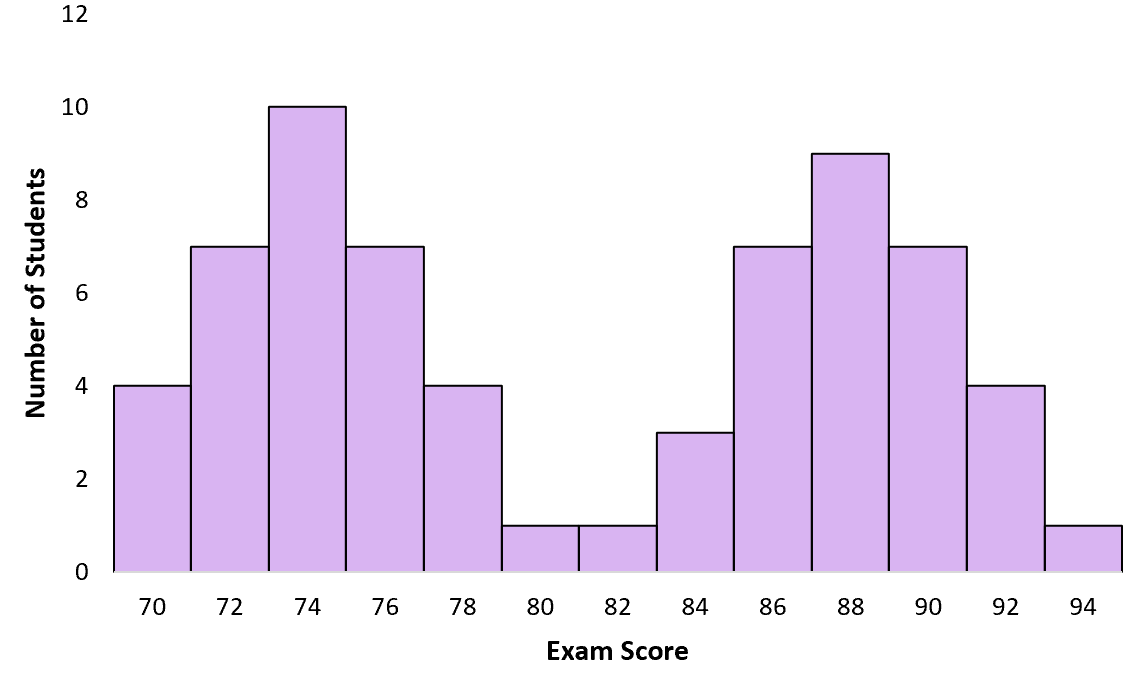
Beispiel 2: Höhe verschiedener Pflanzenarten

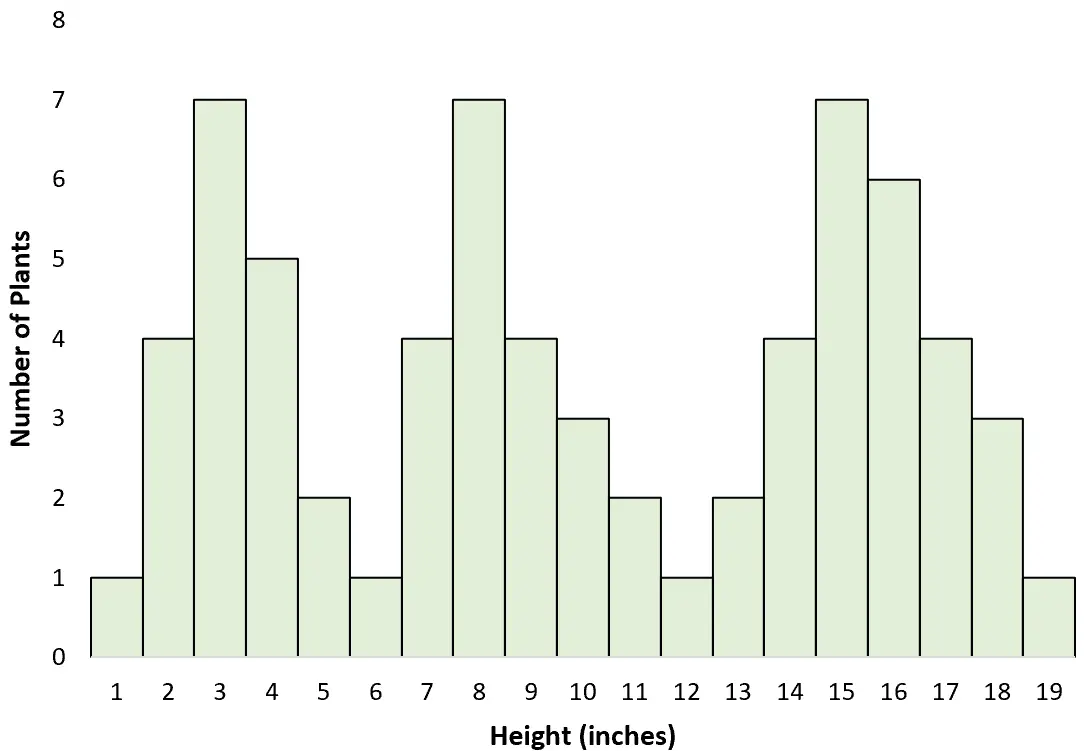
Angenommen, ein Wissenschaftler geht um ein Feld herum und misst die Höhe verschiedener Pflanzen. Ohne es zu merken, misst sie die Größe von drei verschiedenen Arten: einer ziemlich groß, einer mittelgroß und einer ziemlich klein.

Als sie ein Histogramm erstellt, um die Höhenverteilung zu visualisieren, stellt sie fest, dass diese multimodal ist: Jeder Peak repräsentiert die häufigste Höhe der drei verschiedenen Arten.

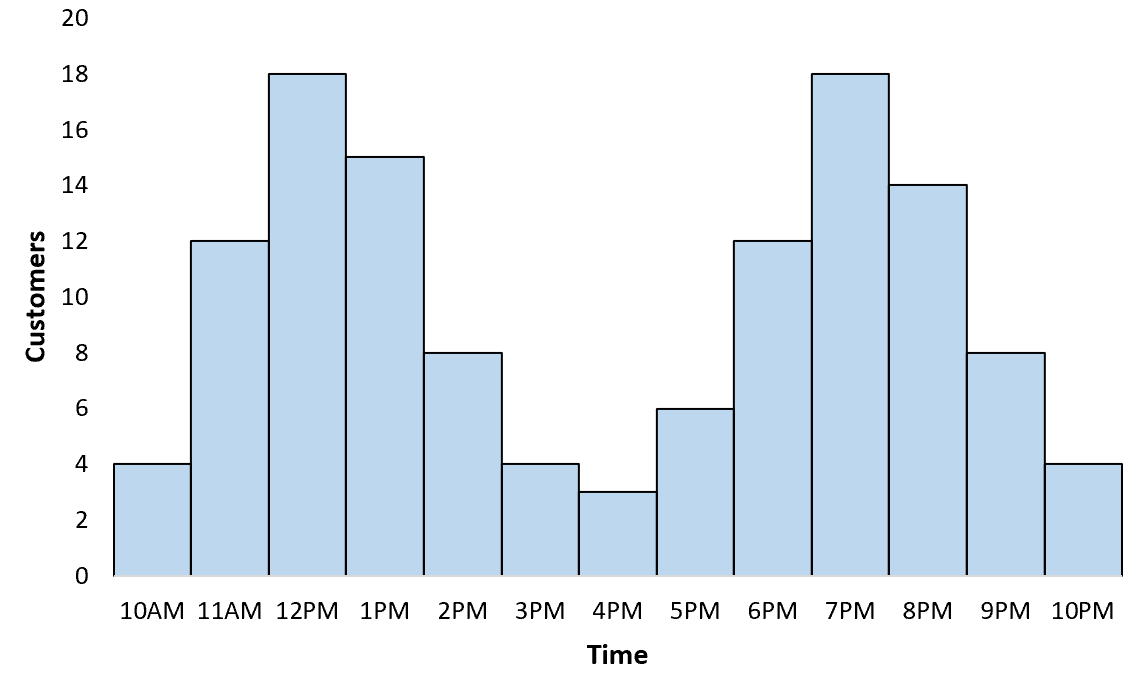
Beispiel 3: Verteilung der Kunden

Ein Restaurantbesitzer verfolgt die Anzahl der Kunden, die ihn stündlich besuchen. Wenn er ein Histogramm erstellt, um die Verteilung der Kunden zu visualisieren, stellt er fest, dass die Verteilung multimodal ist: Es gibt einen Höhepunkt während der Mittagspause und einen weiteren Höhepunkt während der Abendstunden.

Was sind die Ursachen multimodaler Verteilungen?

Meist liegt einer multimodalen Verteilung eine von zwei Ursachen zugrunde:

1. Mehrere Gruppen werden zusammengefasst.

Multimodale Verteilungen können auftreten, wenn Sie Daten für mehrere Gruppen sammeln, ohne es zu merken.

Wenn ein Wissenschaftler beispielsweise unwissentlich die Höhe von drei verschiedenen Pflanzenarten misst, die sich auf demselben Feld befinden, erscheint die Verteilung aller Pflanzen multimodal, wenn sie im selben Histogramm platziert werden.

2. Es gibt ein zugrunde liegendes Phänomen.

Aufgrund bestimmter zugrunde liegender Phänomene kann es auch zu multimodalen Verteilungen kommen.

Beispielsweise folgt die Anzahl der Kunden, die stündlich ein Restaurant besuchen, einer multimodalen Verteilung, da Menschen dazu neigen, zu zwei unterschiedlichen Zeiten in Restaurants zu essen: Mittag- und Abendessen. Dieses zugrunde liegende menschliche Verhalten ist der Ursprung der multimodalen Verteilung.

So analysieren Sie multimodale Verteilungen

Wir beschreiben Verteilungen oft mit dem Mittelwert oder Median, weil uns dies eine Vorstellung davon gibt, wo sich das „Zentrum“ der Verteilung befindet.

Leider sind Mittelwert und Median für eine bimodale Verteilung nicht hilfreich. Beispielsweise beträgt die durchschnittliche Prüfungspunktzahl der Studierenden im obigen Beispiel 81:

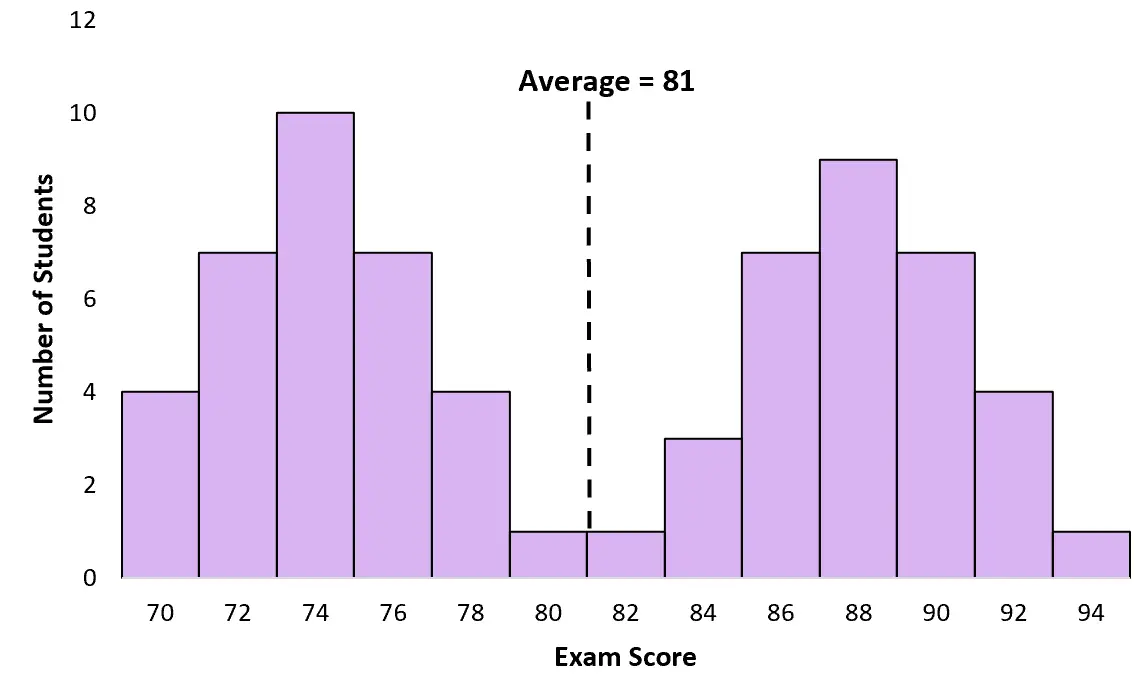
Allerdings erzielten nur sehr wenige Schüler auch nur annähernd 81 Punkte. In diesem Fall ist der Durchschnitt irreführend. Die meisten Schüler erzielten tatsächlich Werte um die 74 oder 88.

Eine bessere Möglichkeit, bimodale Verteilungen zu analysieren und zu interpretieren, besteht darin, die Daten einfach in zwei verschiedene Gruppen zu unterteilen und dann die zentrale Lage und Verteilung für jede Gruppe einzeln zu analysieren.

Beispielsweise können wir Prüfungsergebnisse in „niedrige Punktzahlen“ und „hohe Punktzahlen“ unterteilen und dann den Mittelwert und die Standardabweichung für jede Gruppe ermitteln.

Wenn Sie zusammenfassende Statistiken für eine bestimmte Verteilung wie Mittelwert, Median oder Standardabweichung berechnen, stellen Sie sicher, dass Sie die Verteilung visualisieren, um festzustellen, ob sie unimodal oder multimodal ist.

Wenn eine Verteilung multimodal ist, kann es irreführend sein, sie mithilfe eines einzelnen Mittelwerts, Medians oder einer Standardabweichung zu beschreiben.