Was ist eine unimodale verteilung? (definition & #038; beispiel)

Eine unimodale Verteilung ist eine Wahrscheinlichkeitsverteilung mit einem klaren Peak.

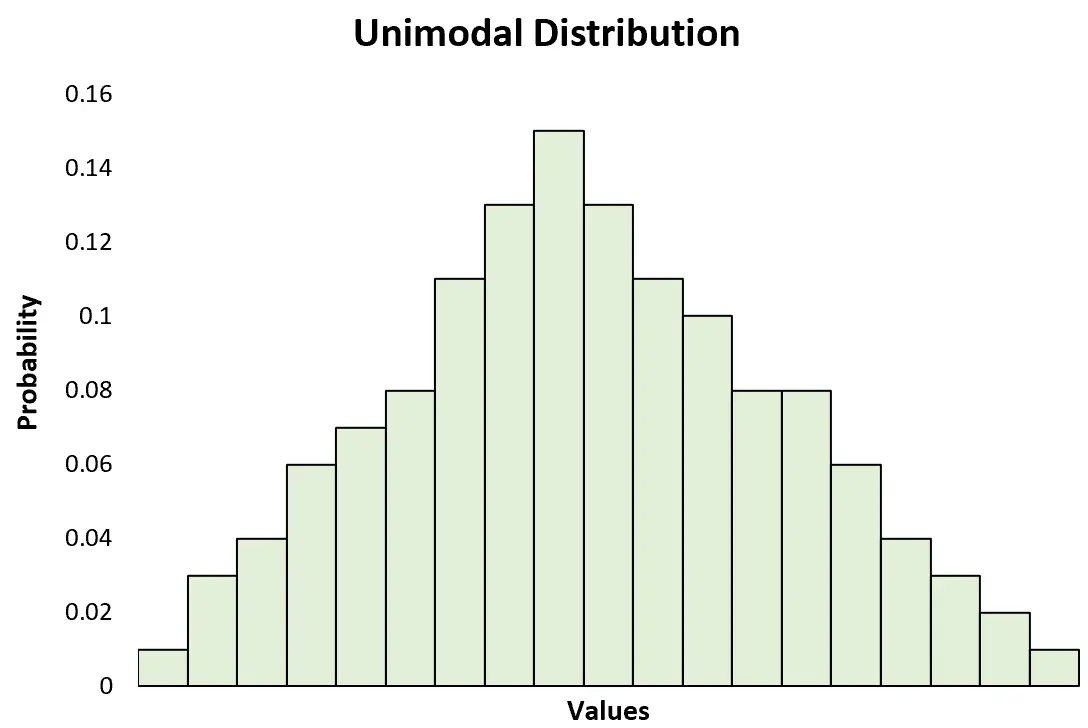
Dies steht im Gegensatz zu einer bimodalen Verteilung , die zwei deutliche Spitzen aufweist:

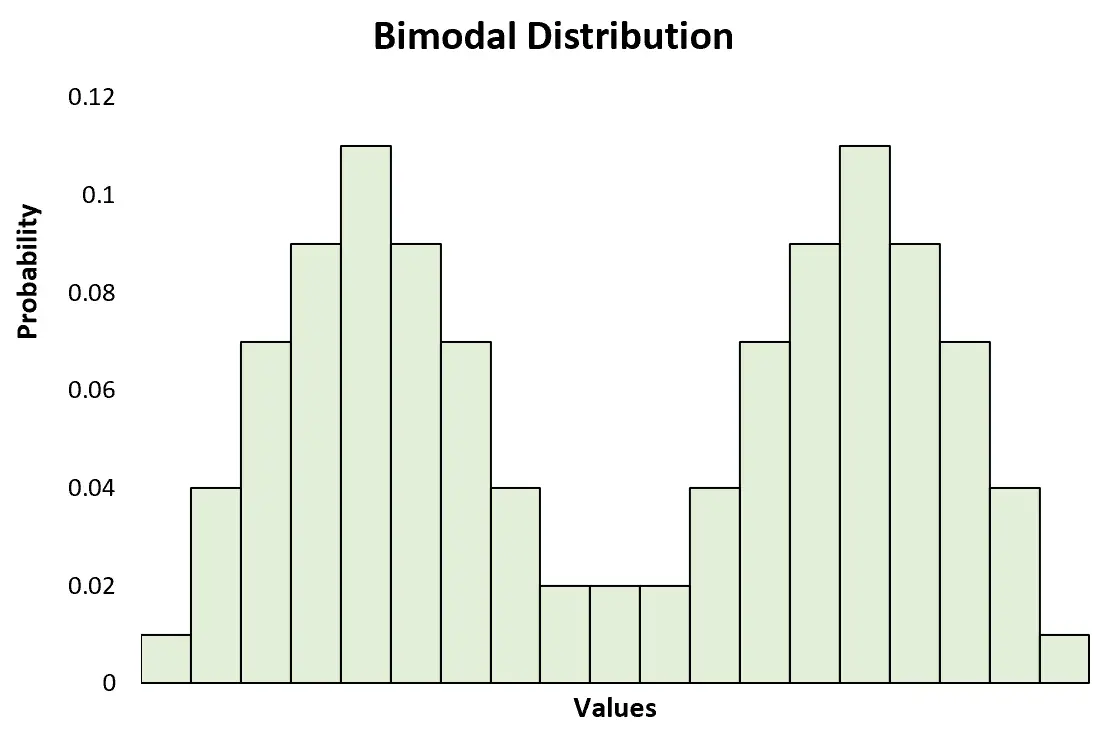
Dies steht auch im Gegensatz zu einer multimodalen Verteilung , die zwei oder mehr Spitzen aufweist:

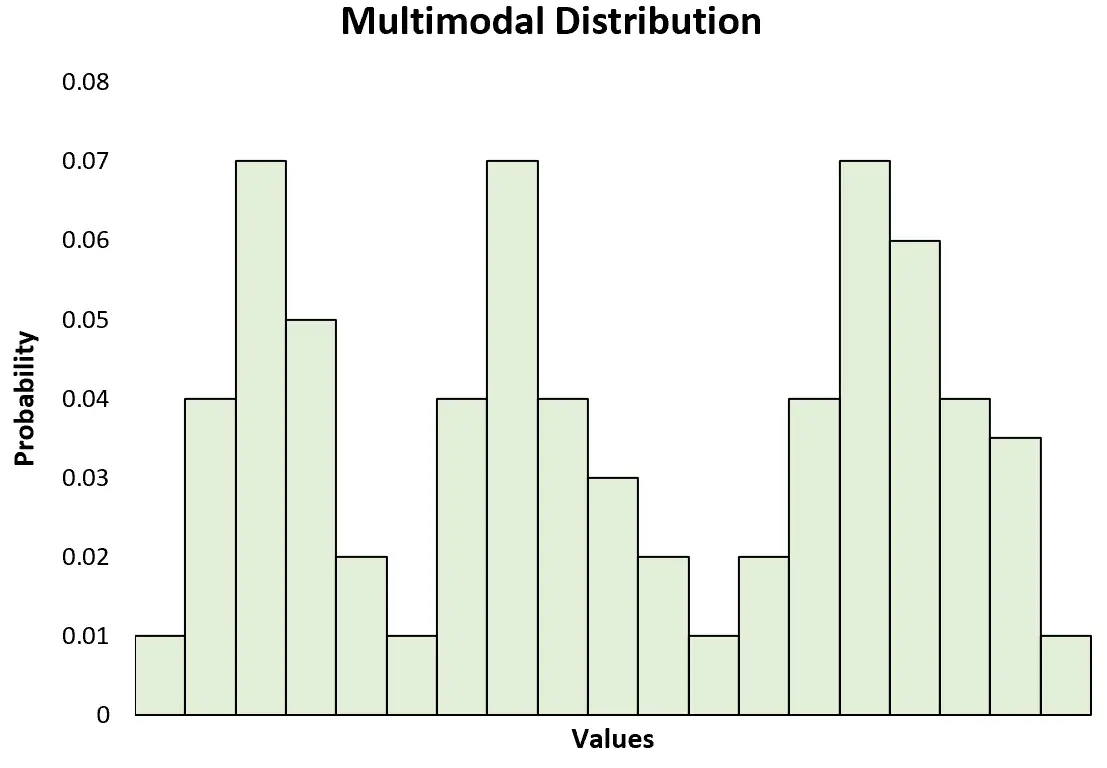
Hinweis: Eine bimodale Verteilung ist nur eine bestimmte Art multimodaler Verteilung.

Beispiele für unimodale Verteilungen

Hier sind einige Beispiele für unimodale Verteilungen in der Praxis.

Beispiel 1: Geburtsgewicht von Babys

Es ist bekannt, dass die Gewichtsverteilung von Neugeborenen einer unimodalen Verteilung mit einem durchschnittlichen Gewicht von etwa 7,5 Pfund folgt. Wenn wir ein Histogramm des Babygewichts erstellen, sehen wir einen „Höchstwert“ bei 7,5 Pfund, wobei einige Babys mehr und andere weniger wiegen.

Beispiel 2: ACT-Ergebnisse

Der durchschnittliche ACT-Wert für High-School-Schüler in den Vereinigten Staaten liegt bei etwa 21, wobei einige Schüler niedrigere und andere höhere Werte erzielen. Wenn wir ein Histogramm der ACT-Ergebnisse aller Schüler in den Vereinigten Staaten erstellen, sehen wir einen einzigen „Höhepunkt“ im Alter von 21 Jahren, mit höheren Werten für einige Schüler und niedrigeren Werten für andere.

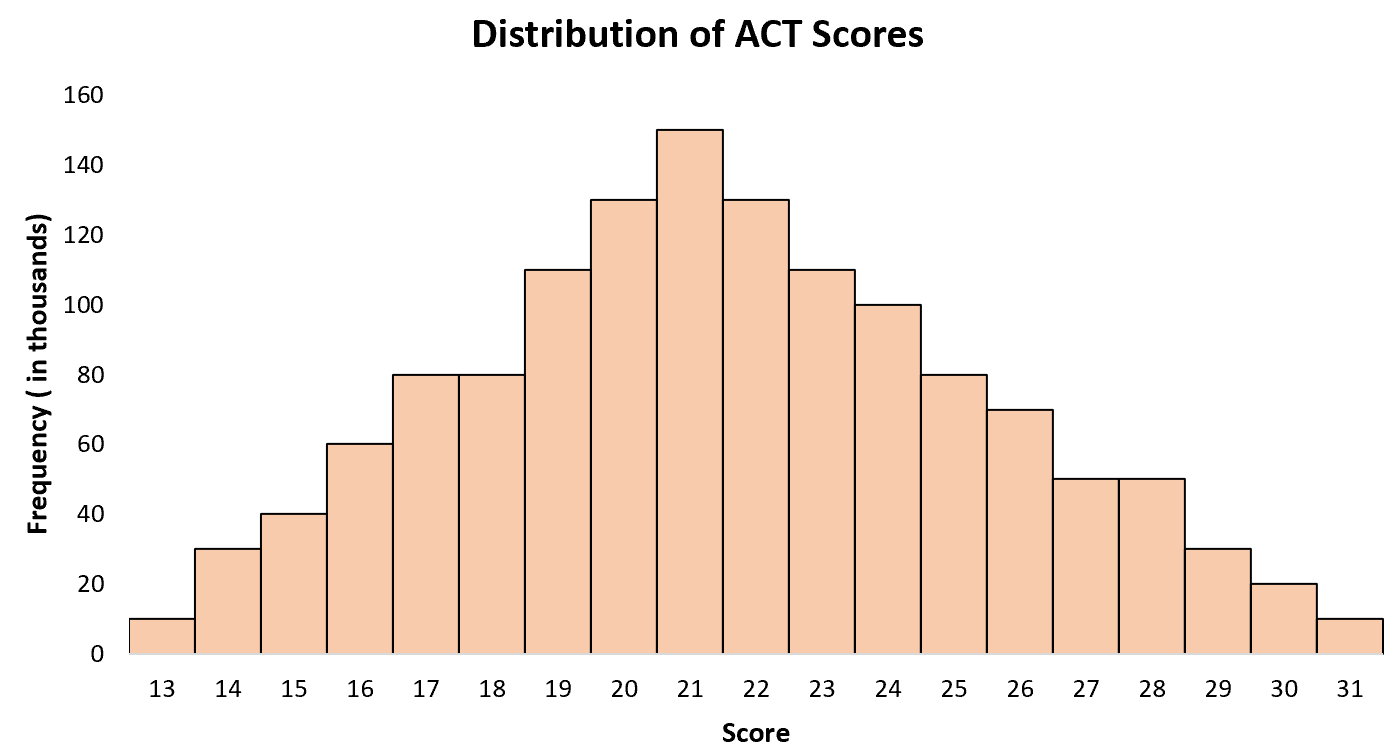
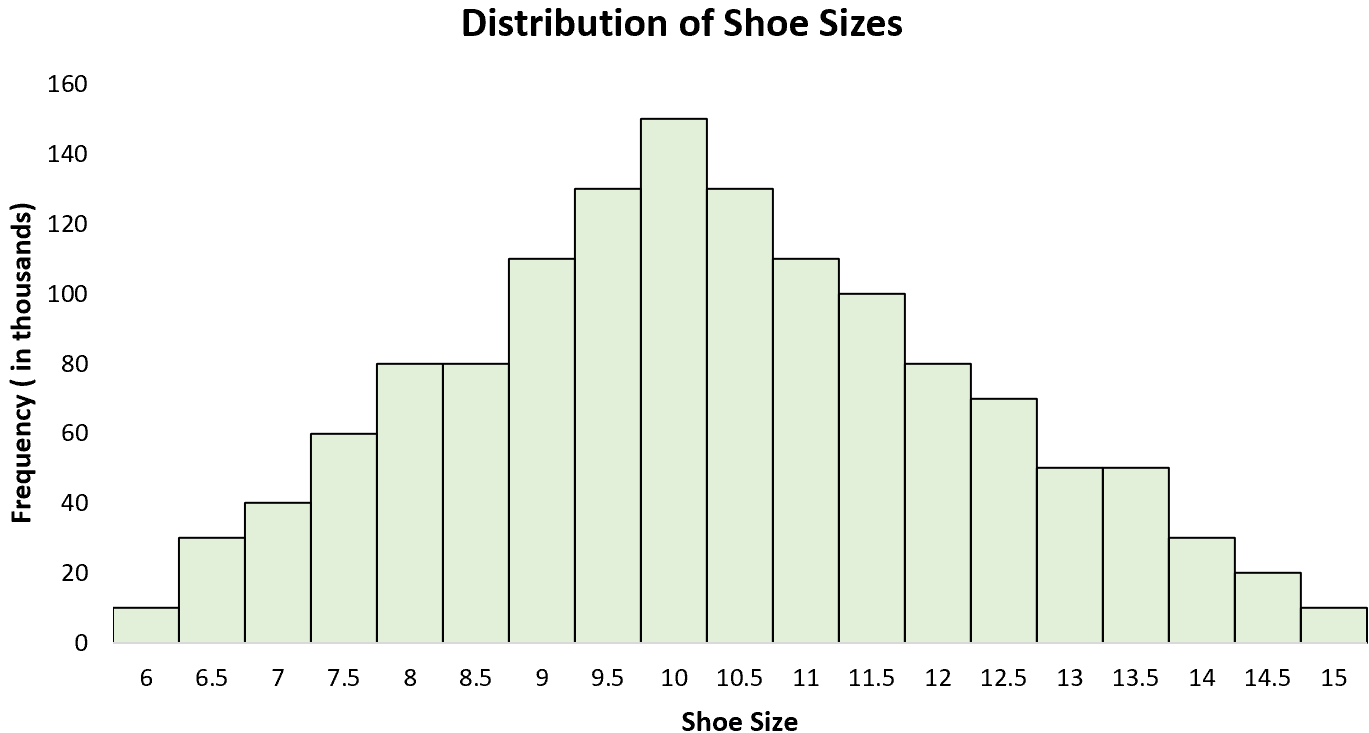
Beispiel 3: Schuhgrößen

Die Verteilung der Herrenschuhgrößen ist eine unimodale Verteilung mit einem „Höchstwert“ bei etwa 10. Wenn wir ein Histogramm aller Herrenschuhgrößen erstellen, sehen wir einen einzelnen Spitzenwert bei 10, wobei einige Männer eine größere Schuhgröße tragen und andere eine größere Größe. kleinere Größe.

Unimodale Verteilungen in der Statistik

Die folgenden Wahrscheinlichkeitsverteilungen in der Statistik sind alle unimodale Verteilungen:

Die Normalverteilung

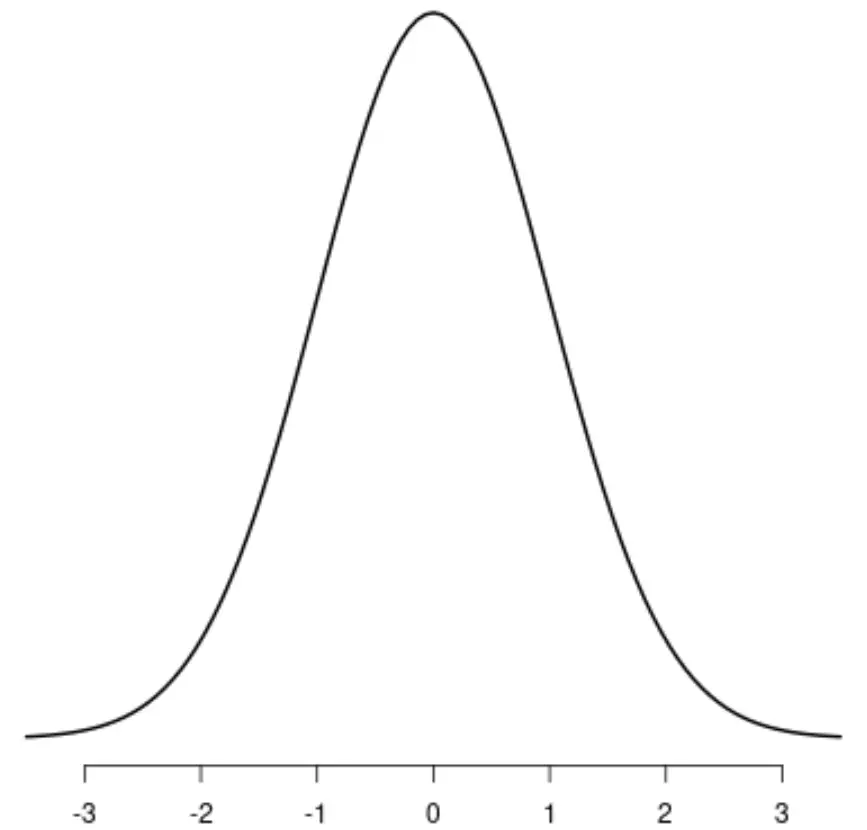
Die Verteilung t

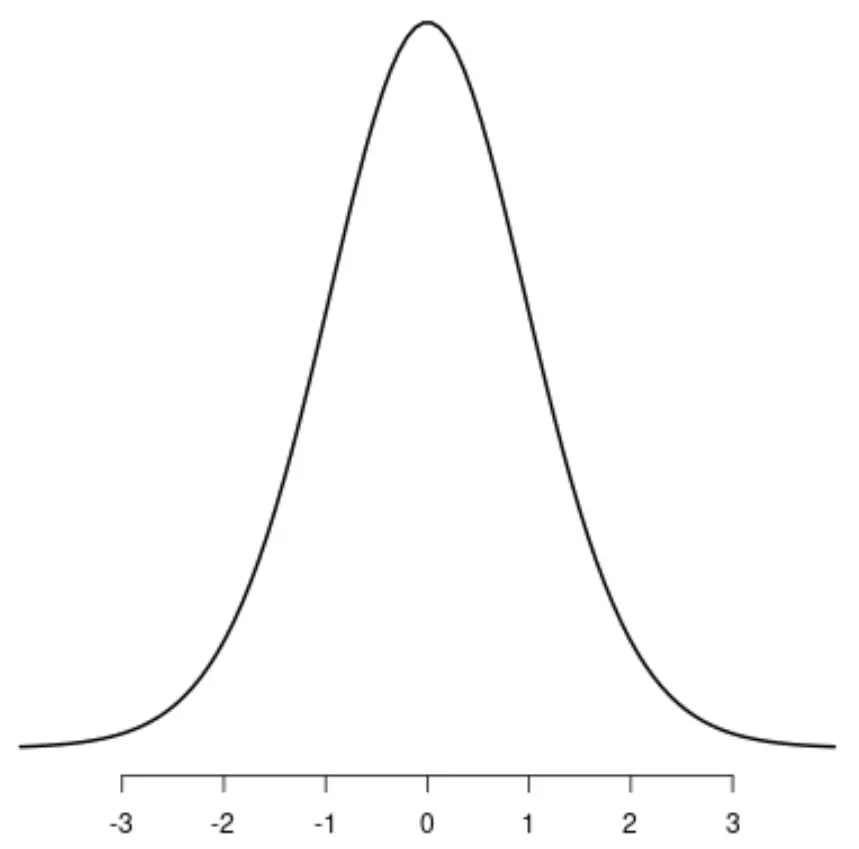
Gleichmäßige Verteilung

Die Cauchy-Verteilung

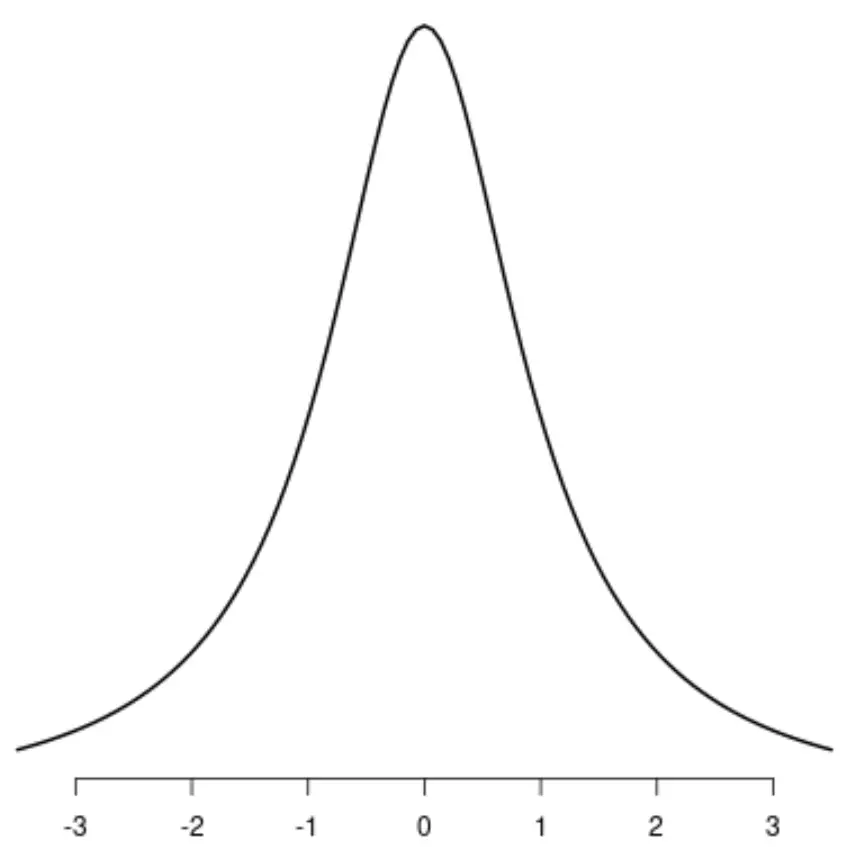
Beachten Sie, dass jede dieser Verteilungen einen einzelnen eindeutigen Peak aufweist.

So analysieren Sie unimodale Verteilungen

Wir beschreiben unimodale Verteilungen oft mit drei verschiedenen Maßen der zentralen Tendenz :

• Durchschnitt : Der Durchschnittswert
• Median : Der Medianwert
• Modus : Der Wert, der am häufigsten erscheint

Je nach Asymmetrie der Verteilung sind diese drei Messungen an unterschiedlichen Orten zu finden.

Linksschiefe Verteilung: Mittelwert < Median < Modus

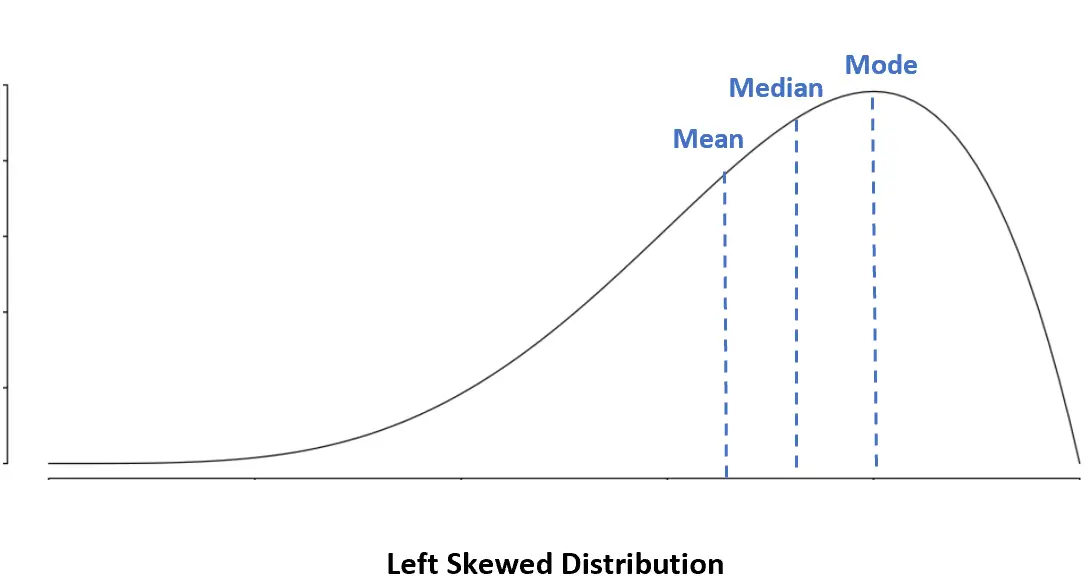
Bei einer linksschiefen Verteilung ist der Mittelwert kleiner als der Median.

Rechtsschiefe Verteilung: Modus < Median < Mittel

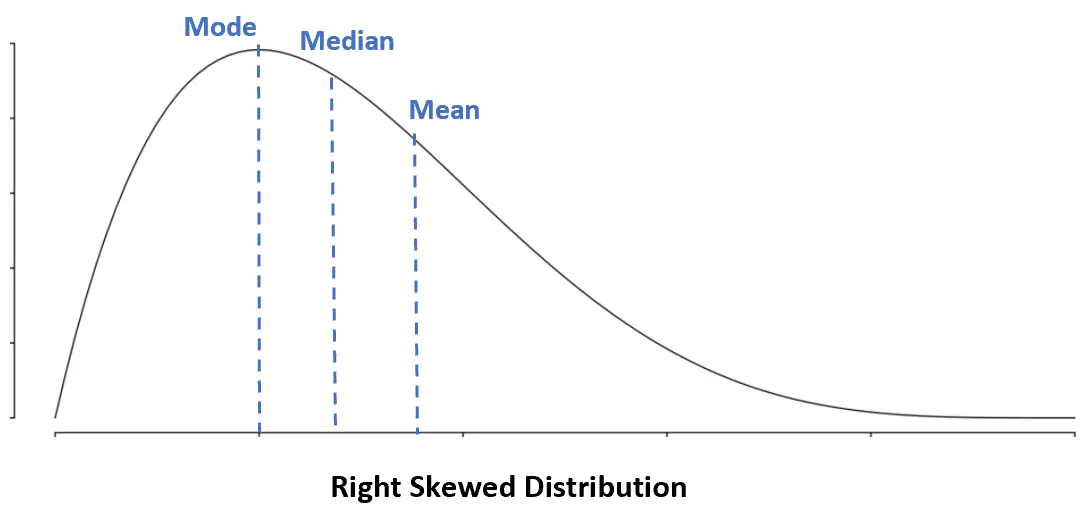
Bei einer rechtsschiefen Verteilung ist der Mittelwert größer als der Median.

Keine Verzerrung: Mittelwert = Median = Modus

Bei einer symmetrischen Verteilung sind Mittelwert, Median und Modus alle gleich.

Zusätzliche Ressourcen

Links- oder rechtsschiefe Verteilungen
Symmetrische Verteilungen: Definition + Beispiele