Eine einführung in die exponentialverteilung

Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung, mit der die Zeit modelliert wird, die wir warten müssen, bis ein bestimmtes Ereignis eintritt.

Mit dieser Verteilung können Fragen beantwortet werden wie:

• Wie lange sollte ein Einzelhändler warten, bis ein Kunde sein Geschäft betritt?
• Wie lange funktioniert ein Laptop noch, bevor er kaputt geht?
• Wie lange funktioniert eine Autobatterie noch, bevor sie leer ist?
• Wie lange sollten wir bis zum nächsten Vulkanausbruch in einer bestimmten Region warten?

In jedem Szenario wollen wir berechnen, wie lange wir warten müssen, bis ein bestimmtes Ereignis eintritt. Somit könnte jedes Szenario mithilfe einer Exponentialverteilung modelliert werden.

Exponentielle Verteilung: PDF und CDF

Wenn eine Zufallsvariable X einer Exponentialverteilung folgt, kann die Wahrscheinlichkeitsdichtefunktion von X wie folgt geschrieben werden:

f (x; λ) = λe ^-λx

Gold:

• λ: der Geschwindigkeitsparameter (berechnet als λ = 1/μ)
• e: Eine Konstante, die ungefähr 2,718 entspricht

Die kumulative Verteilungsfunktion von

F (x; λ) = 1 – e ^-λx

In der Praxis wird der CDF am häufigsten zur Berechnung von Wahrscheinlichkeiten im Zusammenhang mit der Exponentialverteilung verwendet.

Angenommen, die durchschnittliche Anzahl der Minuten zwischen den Ausbrüchen eines bestimmten Geysirs beträgt 40 Minuten. Wie wahrscheinlich ist es, dass wir weniger als 50 Minuten auf einen Ausbruch warten müssen?

Um dieses Problem zu lösen, müssen wir zunächst den Geschwindigkeitsparameter berechnen:

• λ = 1/µ
• λ = 1/40
• λ = 0,025

Wir können λ = 0,025 und x = 50 in die CDF-Formel einsetzen:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

Die Wahrscheinlichkeit, dass wir weniger als 50 Minuten auf den nächsten Ausbruch warten müssen, beträgt 0,7135 .

Visualisieren Sie die Exponentialverteilung

Die folgende Grafik zeigt die Wahrscheinlichkeitsdichtefunktion einer Zufallsvariablen

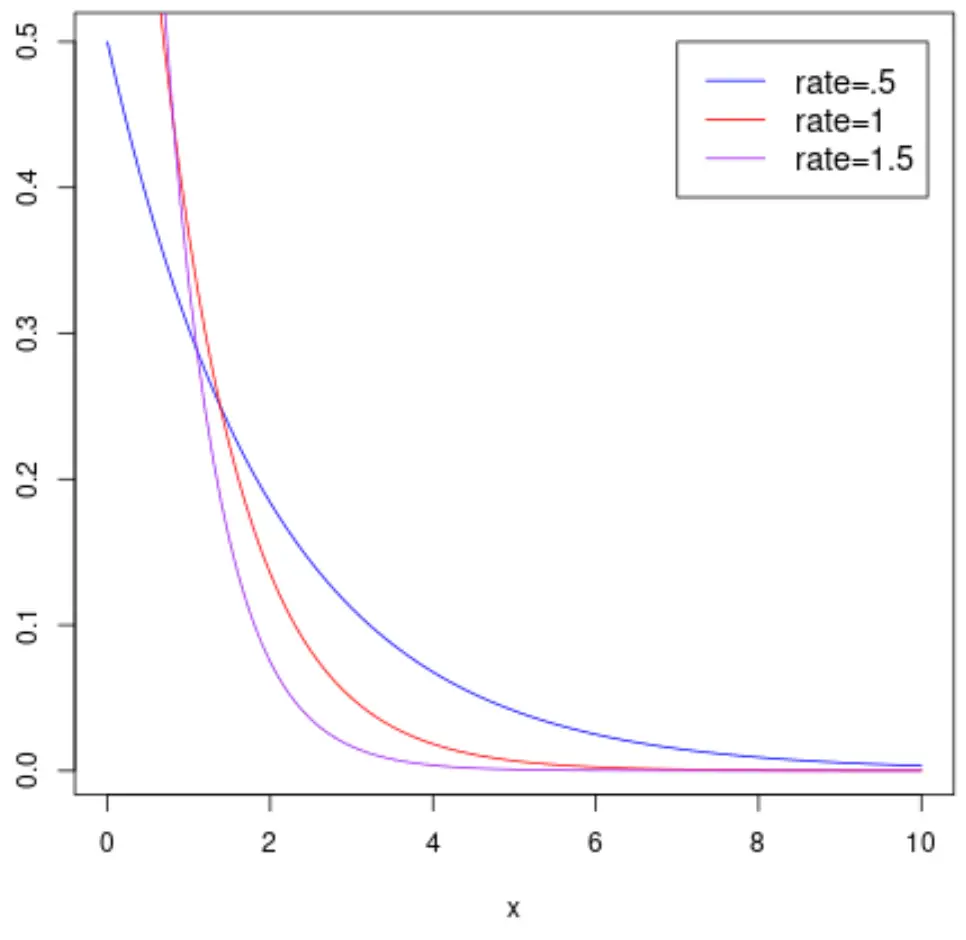
Und die folgende Grafik zeigt die kumulative Verteilungsfunktion einer Zufallsvariablen X , die einer Exponentialverteilung mit unterschiedlichen Ratenparametern folgt:

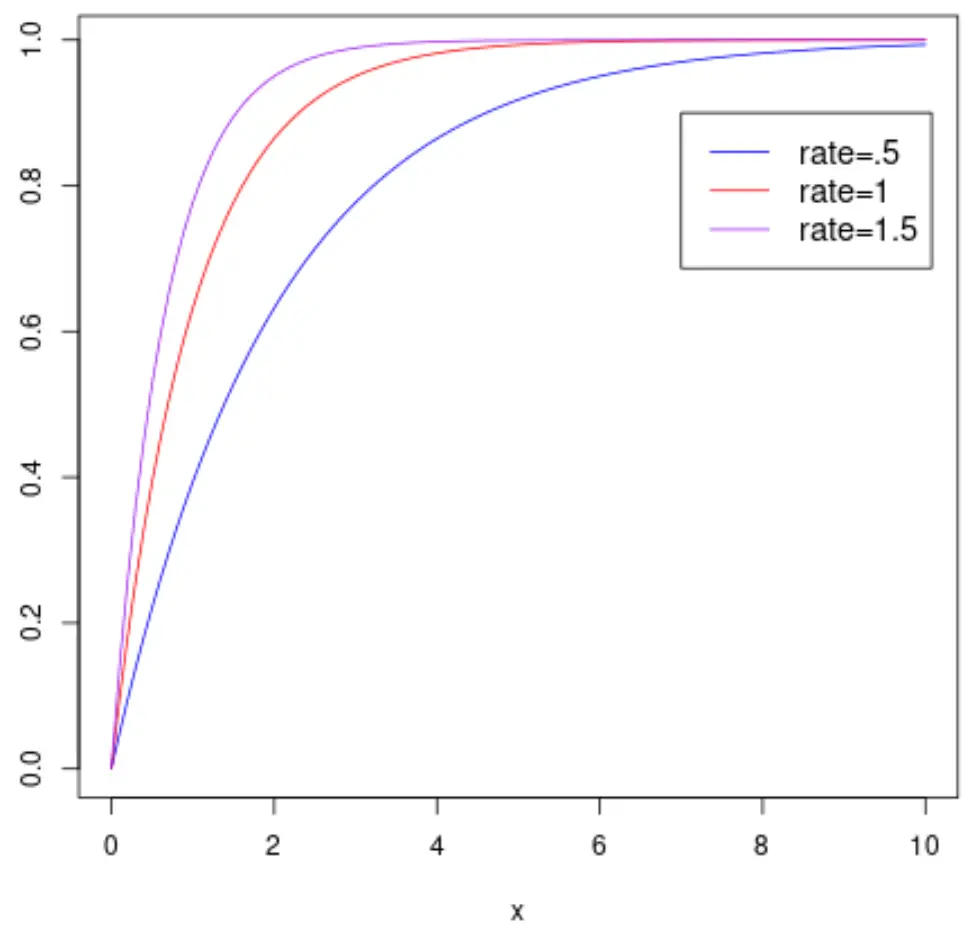
Hinweis: Sehen Sie sich dieses Tutorial an, um zu erfahren, wie Sie eine Exponentialverteilung in R zeichnen.

Eigenschaften der Exponentialverteilung

Die Exponentialverteilung hat folgende Eigenschaften:

• Durchschnitt: 1 / λ
• Differenz: 1 / λ ²

Angenommen, die durchschnittliche Anzahl der Minuten zwischen den Ausbrüchen eines bestimmten Geysirs beträgt 40 Minuten. Wir würden die Rate als λ = 1/μ = 1/40 = 0,025 berechnen.

Wir könnten dann die folgenden Eigenschaften für diese Verteilung berechnen:

• Durchschnittliche Wartezeit für den nächsten Ausbruch: 1/λ = 1 /.025 = 40
• Variation der Wartezeiten für den nächsten Ausbruch: 1/λ ² = 1 /.025 ² = 1600

Hinweis: Die Exponentialverteilung hat auch die Eigenschaft der Gedächtnislosigkeit , was bedeutet, dass die Wahrscheinlichkeit des Eintretens eines zukünftigen Ereignisses nicht durch das Eintreten vergangener Ereignisse beeinflusst wird.

Probleme der Exponentialverteilungspraxis

Verwenden Sie die folgenden Übungsaufgaben, um Ihr Wissen über die Exponentialverteilung zu testen.

Frage 1: Durchschnittlich alle zwei Minuten betritt ein neuer Kunde ein Geschäft. Bestimmen Sie nach der Ankunft eines Kunden die Wahrscheinlichkeit, dass in weniger als einer Minute ein neuer Kunde eintrifft.

Lösung 1: Die durchschnittliche Zeit zwischen Clients beträgt zwei Minuten. Somit kann der Satz wie folgt berechnet werden:

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Wir können λ = 0,5 und x = 1 in die CDF-Formel einsetzen:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• P(X ≤ 1) = 0,3935

Die Wahrscheinlichkeit, dass wir weniger als eine Minute auf den nächsten Kunden warten müssen, beträgt 0,3935 .

Frage 2: In einer bestimmten Region kommt es durchschnittlich alle 400 Tage zu einem Erdbeben. Bestimmen Sie nach einem Erdbeben die Wahrscheinlichkeit, dass es mehr als 500 Tage dauert, bis das nächste Erdbeben auftritt.

Lösung 2: Die durchschnittliche Zeit zwischen Erdbeben beträgt 400 Tage. Somit kann der Satz wie folgt berechnet werden:

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Wir können λ = 0,0025 und x = 500 in die CDF-Formel einsetzen:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,0025(500)
• P(X ≤ 1) = 0,7135

Die Wahrscheinlichkeit, dass wir weniger als 500 Tage auf das nächste Erdbeben warten müssen, beträgt 0,7135. Die Wahrscheinlichkeit, dass wir mehr als 500 Tage auf das nächste Erdbeben warten müssen, beträgt also 1 – 0,7135 = 0,2865 .

Frage 3: Ein Callcenter erhält durchschnittlich alle 10 Minuten einen neuen Anruf. Bestimmen Sie nach einem Kundenanruf die Wahrscheinlichkeit, dass innerhalb von 10 bis 15 Minuten ein neuer Kunde anruft.

Lösung 3: Die durchschnittliche Zeit zwischen Anrufen beträgt 10 Minuten. Somit kann der Satz wie folgt berechnet werden:

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Mit der folgenden Formel können wir die Wahrscheinlichkeit berechnen, dass ein neuer Kunde innerhalb von 10-15 Minuten anruft:

• P(10 < X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 < X ≤ 15) = 0,7769 – 0,6321
• P(10 < X ≤ 15) = 0,1448

Die Wahrscheinlichkeit, dass ein neuer Kunde innerhalb von 10–15 Minuten anruft. ist 0,1448 .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten Einführungen in andere gängige Wahrscheinlichkeitsverteilungen.

Eine Einführung in die Normalverteilung
Eine Einführung in die Binomialverteilung
Eine Einführung in die Poisson-Verteilung
Eine Einführung in die Gleichverteilung