Berkson-voreingenommenheit: definition + beispiele

Berkson-Bias ist eine Art von Bias, die in der Forschung auftritt, wenn zwei Variablen in den Daten einer Stichprobe scheinbar negativ korrelieren, in der Gesamtpopulation jedoch tatsächlich positiv korreliert sind.

Angenommen, Tom möchte den Zusammenhang zwischen der Qualität von Hamburgern und Milchshakes in lokalen Restaurants untersuchen.

Es geht los und sammelt die folgenden Daten zu sieben verschiedenen Restaurants:

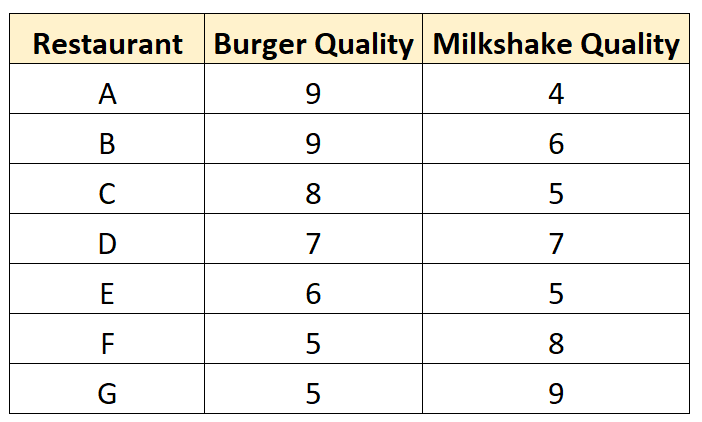
Es erstellt ein Streudiagramm zur Visualisierung der Daten:

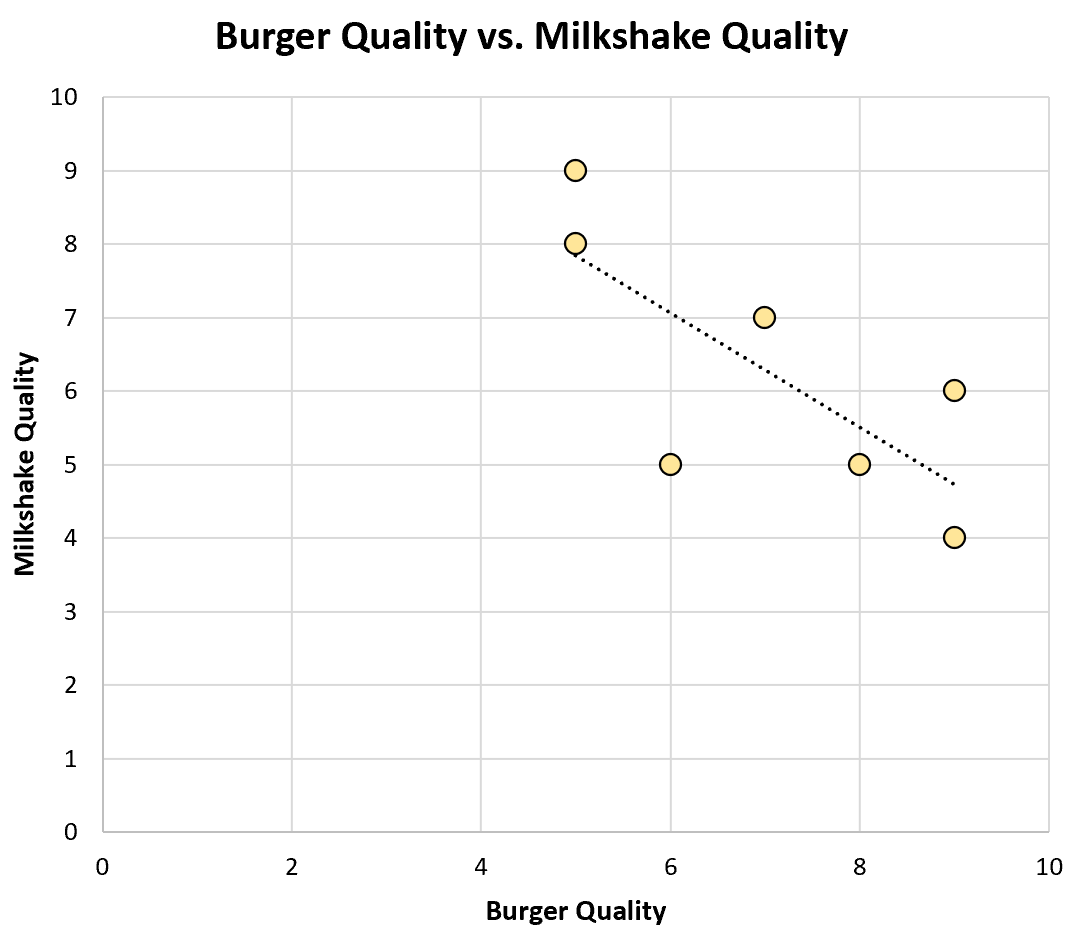
Der Pearson-Korrelationskoeffizient zwischen diesen beiden Variablen beträgt -0,75 , was einer starken negativen Korrelation entspricht.

Für Tom widerspricht diese Entdeckung der Intuition: Er würde denken, dass Restaurants, die gute Hamburger machen, auch gute Milchshakes machen.

Es stellt sich jedoch heraus, dass Tom alle Restaurants in der Stadt, die sowohl schlechte Burger als auch schlechte Milchshakes anbieten, einfach ignoriert hat.

Hätte er diese Restaurants besucht, hätte er folgenden Datensatz gesammelt:

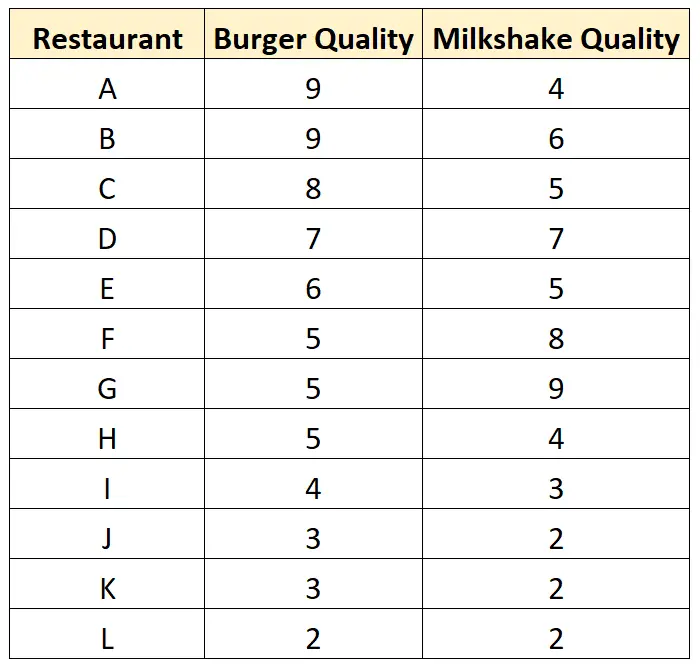
Und so sieht ein Streudiagramm für diesen Datensatz aus:

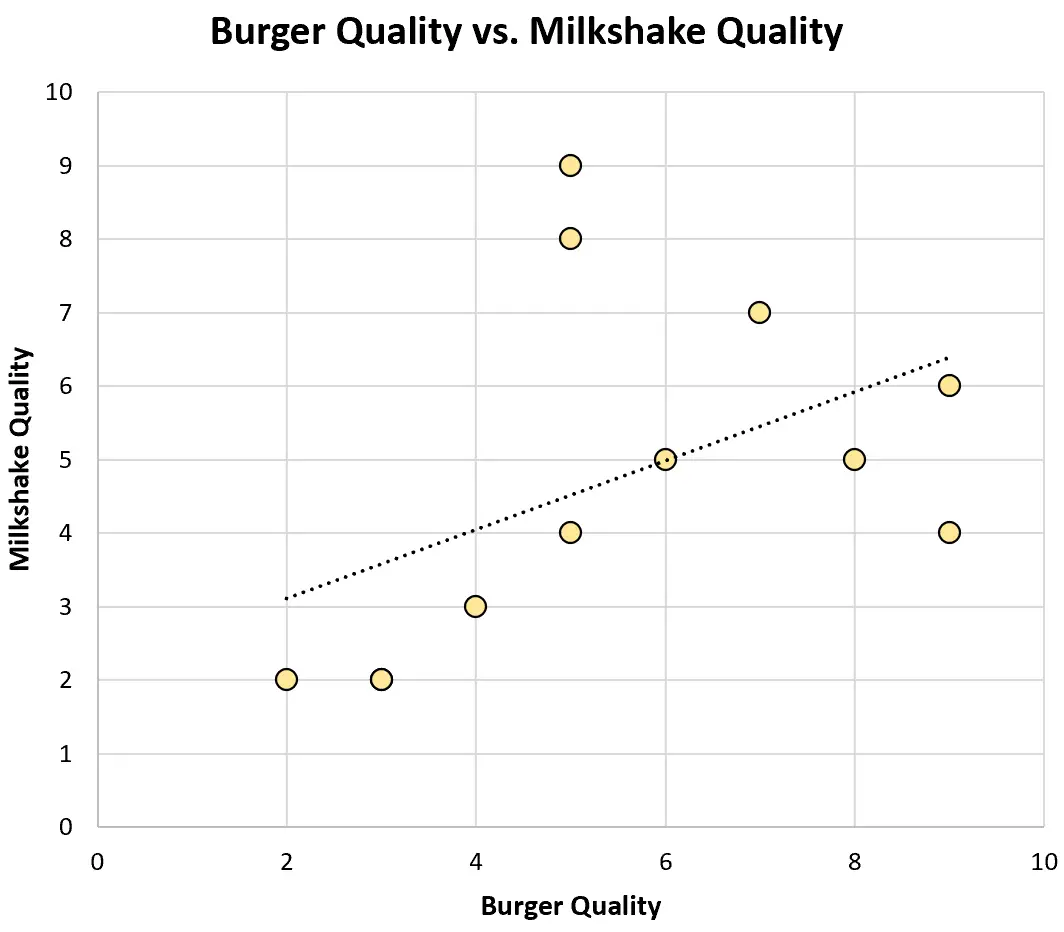
Der Pearson-Korrelationskoeffizient zwischen den beiden Variablen beträgt 0,46 , was einer mäßig starken positiven Korrelation entspricht.

Indem er nur einen Teil der Restaurants der Stadt untersuchte, kam Tom fälschlicherweise zu dem Schluss, dass ein negativer Zusammenhang zwischen der Qualität von Burgern und Milchshakes bestehe.

Tatsächlich stellt sich heraus, dass (wie zu erwarten) eine positive Beziehung zwischen diesen beiden Variablen besteht. Dies ist ein klassisches Beispiel für Berksons Voreingenommenheit.

In den folgenden Beispielen finden Sie weitere Szenarien, in denen in der Praxis ein Berkson-Bias auftritt.

Beispiel 1: Hochschulzulassungen

Angenommen, eine Hochschule nimmt nur Studenten auf, die einen ausreichend hohen Notendurchschnitt und ACT-Wert haben.

Es ist bekannt, dass diese beiden Variablen positiv korrelieren, aber es zeigt sich, dass bei Studenten, die sich für den Besuch einer bestimmten Hochschule entscheiden, offenbar eine negative Korrelation zwischen beiden besteht.

Dieser negative Zusammenhang tritt jedoch nur auf, weil Studierende mit einem hohen GPA- und ACT-Ergebnis eine Eliteuniversität besuchen können, während Studierende mit einem niedrigen GPA- und ACT-Ergebnis überhaupt nicht zugelassen werden.

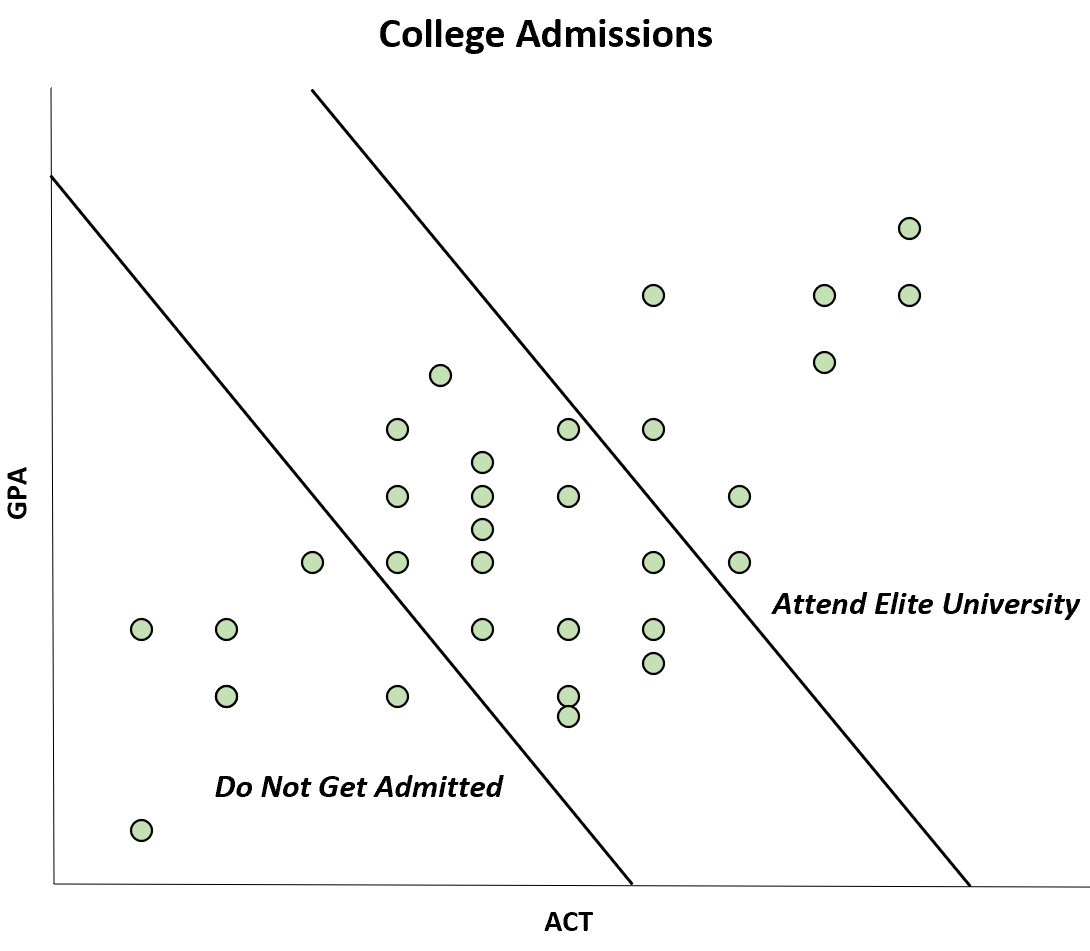
Obwohl die Korrelation zwischen ACT und GPA in der Bevölkerung positiv ist, scheint die Korrelation in der Stichprobe negativ zu sein. Dies ist ein Fall von Voreingenommenheit seitens Berkson.

Beispiel 2: Dating-Präferenzen

Viele Menschen gehen nur mit Partnern aus, die sowohl attraktiv sind als auch eine gute Persönlichkeit haben.

In der realen Welt besteht möglicherweise keine Korrelation zwischen diesen beiden Variablen, aber wenn man den Dating-Pool einschränkt, ignoriert eine Person möglicherweise potenzielle Partner, die sowohl unattraktiv als auch begabt sind, völlig. „Eine gute Persönlichkeit.“

Bei potenziellen Partnern könnte es also so aussehen, als gäbe es einen negativen Zusammenhang zwischen diesen beiden Variablen: Attraktivere Menschen haben schlechtere Persönlichkeiten, und Menschen mit besseren Persönlichkeiten scheinen weniger attraktiv zu sein.

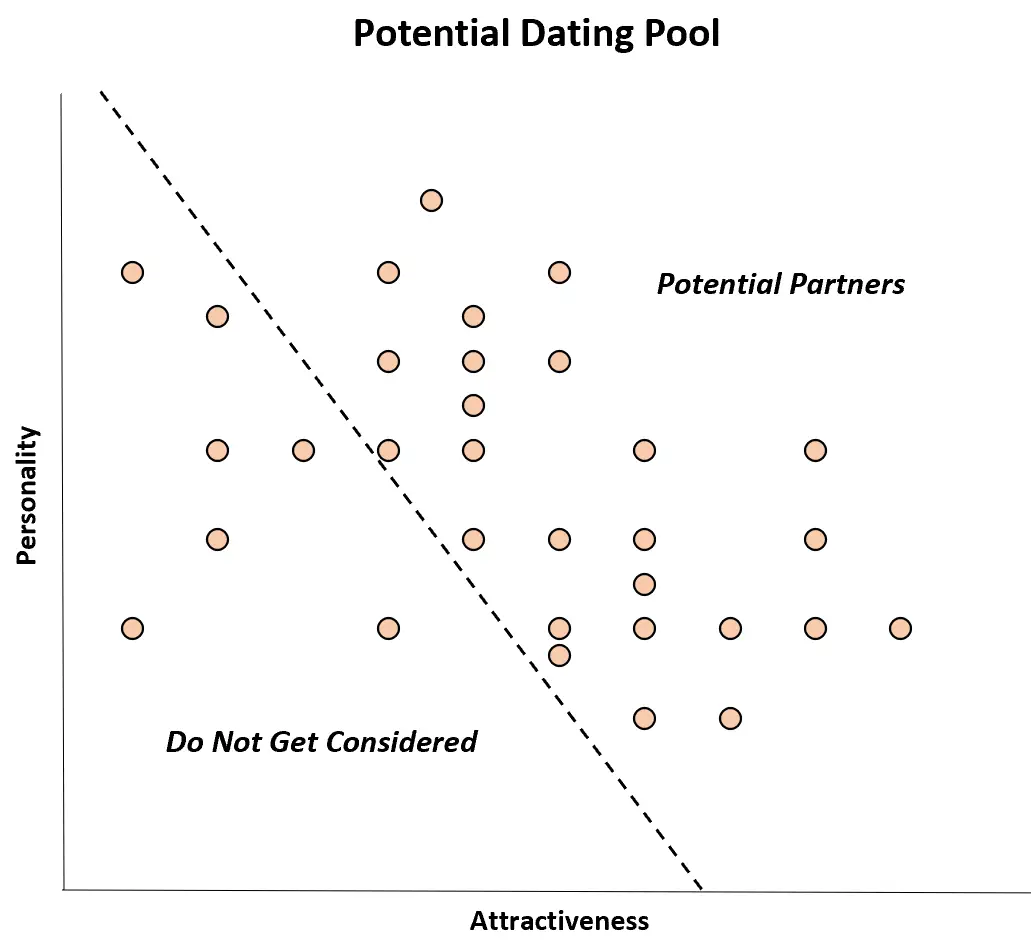
Obwohl zwischen diesen beiden Variablen in der Grundgesamtheit keine Korrelation besteht, scheint es in der Stichprobe potenzieller Partner eine negative Korrelation zu geben. Das ist einfach ein Fall von Berksons Voreingenommenheit.

So verhindern Sie Berksons Voreingenommenheit

Der offensichtlichste Weg, Berkson-Bias in Forschungsstudien zu vermeiden, besteht darin, eine einfache Zufallsstichprobe aus einer Population zu sammeln. Mit anderen Worten: Stellen Sie sicher, dass jedes Mitglied der interessierenden Grundgesamtheit die gleichen Chancen hat, in die Stichprobe aufgenommen zu werden.

Wenn Sie beispielsweise die Krankheitsprävalenz in einem bestimmten Land untersuchen, müssen Sie eine Stichprobe von Personen aus dem ganzen Land sammeln, nicht nur von Personen, die in Krankenhäusern leicht zu erreichen sind.

Durch die Verwendung einer einfachen Zufallsstichprobe können Forscher die Chance maximieren, dass ihre Stichprobe für die Bevölkerung repräsentativ ist, was bedeutet, dass sie ihre Ergebnisse aus der Stichprobe sicher auf die Gesamtbevölkerung übertragen können.