So berechnen sie die gepoolte varianz in r
In der Statistik bezeichnet Clustervarianz den Durchschnitt von zwei oder mehr Clustervarianzen.
Wir verwenden das Wort „gepoolt“, um anzuzeigen, dass wir zwei oder mehr Gruppenvarianzen „poolen“, um eine einzige Zahl für die gemeinsame Varianz zwischen den Gruppen zu erhalten.
In der Praxis wird die gepoolte Varianz am häufigsten in einem T-Test mit zwei Stichproben verwendet, mit dem ermittelt werden soll, ob die Mittelwerte zweier Grundgesamtheiten gleich sind oder nicht.
Die gepoolte Varianz zwischen zwei Stichproben wird im Allgemeinen mit sp 2 bezeichnet und wie folgt berechnet:
s p 2 = ( (n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
Leider gibt es keine integrierte Funktion zur Berechnung der gepoolten Varianz zwischen zwei Gruppen in R, aber wir können sie ganz einfach berechnen.
Angenommen, wir möchten die gepoolte Varianz zwischen den folgenden zwei Gruppen berechnen:
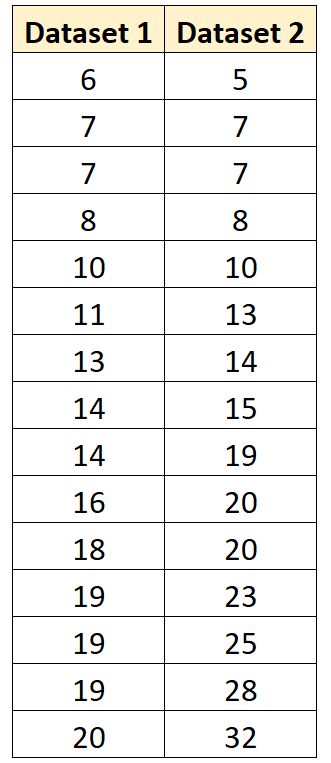
Der folgende Code zeigt, wie die gepoolte Varianz zwischen diesen Gruppen in R berechnet wird:
#define groups of data x1 <- c(6, 7, 7, 8, 10, 11, 13, 14, 14, 16, 18, 19, 19, 19, 20) x2 <- c(5, 7, 7, 8, 10, 13, 14, 15, 19, 20, 20, 23, 25, 28, 32) #calculate sample size of each group n1 <- length(x1) n2 <- length(x2) #calculate sample variance of each group var1 <- var(x1) var2 <- var(x2) #calculate pooled variance between the two groups pooled <- ((n1-1)*var1 + (n2-1)*var2) / (n1+n2-2) #display pooled variance pooled [1] 46.97143
Die gepoolte Varianz zwischen diesen beiden Gruppen beträgt 46,97143 .
Zusätzliche Ressourcen
Was ist Clustervarianz? (Definition und Beispiel)
Gebündelter Gap-Rechner
So berechnen Sie die gepoolte Varianz in Excel