Anova vs. regression: was ist der unterschied?
Zwei in der Statistik häufig verwendete Modelle sind ANOVA- und Regressionsmodelle.
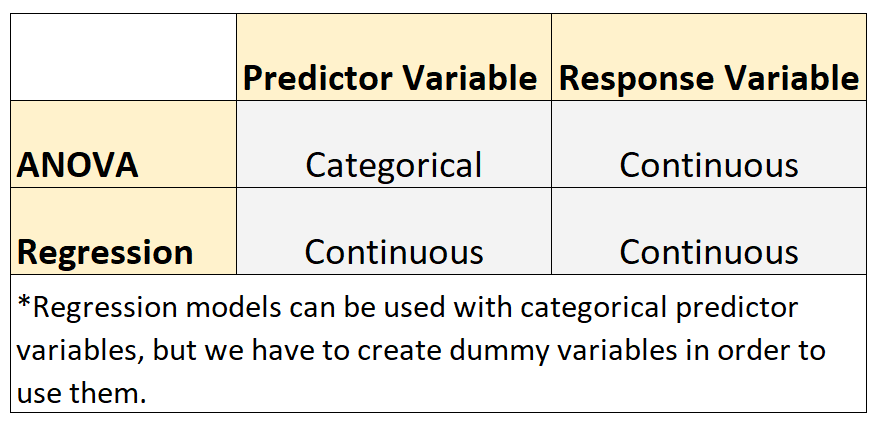
Diese beiden Modelltypen haben die folgende Ähnlichkeit:
- Die Antwortvariable in jedem Modell ist kontinuierlich. Beispiele für kontinuierliche Variablen sind Gewicht, Größe, Länge, Breite, Zeit, Alter usw.
Diese beiden Modelltypen weisen jedoch den folgenden Unterschied auf:
- ANOVA-Modelle werden verwendet, wenn die Prädiktorvariablen kategorial sind. Beispiele für kategoriale Variablen sind Bildungsniveau, Augenfarbe, Familienstand usw.
- Regressionsmodelle werden verwendet, wenn die Prädiktorvariablen kontinuierlich sind.*
*Regressionsmodelle können mit kategorialen Prädiktorvariablen verwendet werden, aber wir müssen Dummy-Variablen erstellen, um sie zu verwenden.
Die folgenden Beispiele zeigen, wann ANOVA- oder Regressionsmodelle in der Praxis eingesetzt werden sollten.
Beispiel 1: Bevorzugtes ANOVA-Modell
Angenommen, ein Biologe möchte verstehen, ob vier verschiedene Düngemittel über einen Zeitraum von einem Monat zum gleichen durchschnittlichen Pflanzenwachstum (in Zoll) führen. Um dies zu testen, trägt sie jeden Dünger auf 20 Pflanzen auf und zeichnet das Wachstum jeder Pflanze nach einem Monat auf.
In diesem Szenario muss der Biologe ein einfaktorielles ANOVA-Modell verwenden, um die Unterschiede zwischen Düngemitteln zu analysieren, da es eine Prädiktorvariable gibt und diese kategorisch ist.
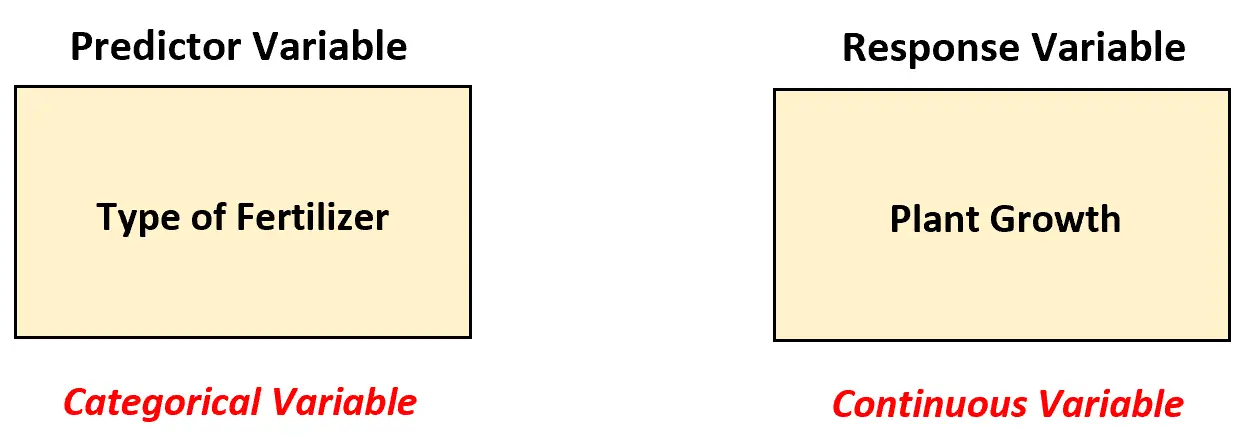
Mit anderen Worten, die Werte der Prädiktorvariablen können in die folgenden „Kategorien“ eingeteilt werden:
- Dünger 1
- Dünger 2
- Dünger 3
- Dünger 4
Eine einfaktorielle ANOVA gibt dem Biologen Auskunft darüber, ob das durchschnittliche Pflanzenwachstum bei den vier verschiedenen Düngemitteln gleich ist oder nicht.
Beispiel 2: Bevorzugtes Regressionsmodell
Nehmen wir an, ein Immobilienmakler möchte den Zusammenhang zwischen Quadratmeterzahl und Immobilienpreis verstehen. Um diesen Zusammenhang zu analysieren, sammelt er Daten über die Quadratmeterzahl und den Preis von 200 Häusern in einer bestimmten Stadt.
In diesem Szenario sollte der Immobilienmakler ein einfaches lineares Regressionsmodell verwenden, um die Beziehung zwischen diesen beiden Variablen zu analysieren, da die Prädiktorvariable (Quadratmeterzahl) kontinuierlich ist.
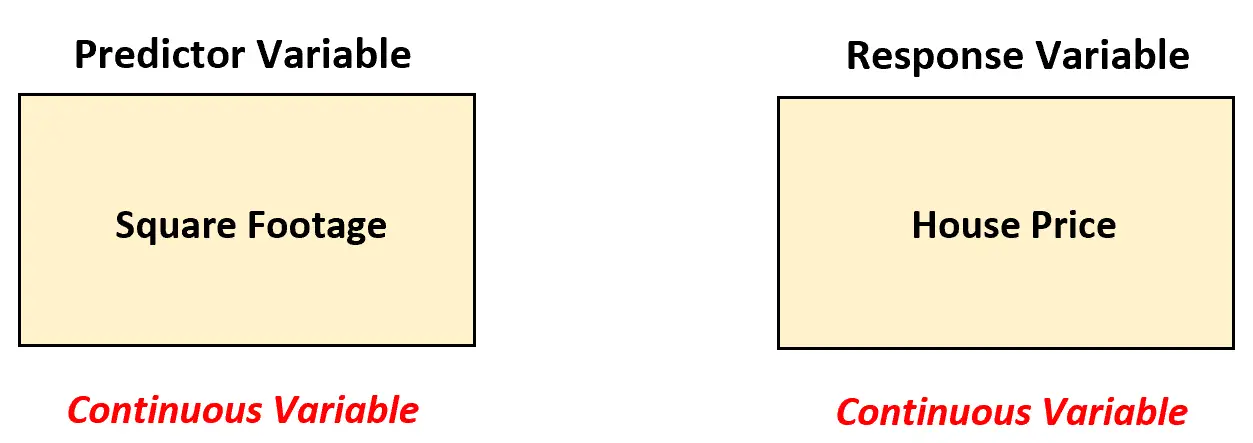
Mithilfe einer einfachen linearen Regression kann der Immobilienmakler das folgende Regressionsmodell anpassen:
Immobilienpreis = β 0 + β 1 (quadratische Fläche)
Der Wert von β 1 stellt die durchschnittliche Änderung des Hauspreises dar, die mit jedem zusätzlichen Quadratfuß einhergeht.
Dadurch kann der Immobilienmakler das Verhältnis zwischen Quadratmeterzahl und Immobilienpreis quantifizieren.
Beispiel 3: Regressionsmodell mit bevorzugten Dummy-Variablen
Angenommen, ein Immobilienmakler möchte die Beziehung zwischen den Prädiktorvariablen „Quadratmeterzahl“ und „Haustyp“ (Einfamilienhaus, Wohnung, Stadthaus) mit der Antwortvariablen Immobilienpreis verstehen.
In diesem Szenario kann der Immobilienmakler eine multiple lineare Regression verwenden, indem er „Heimtyp“ in eine Dummy-Variable umwandelt, da es sich derzeit um eine kategoriale Variable handelt.
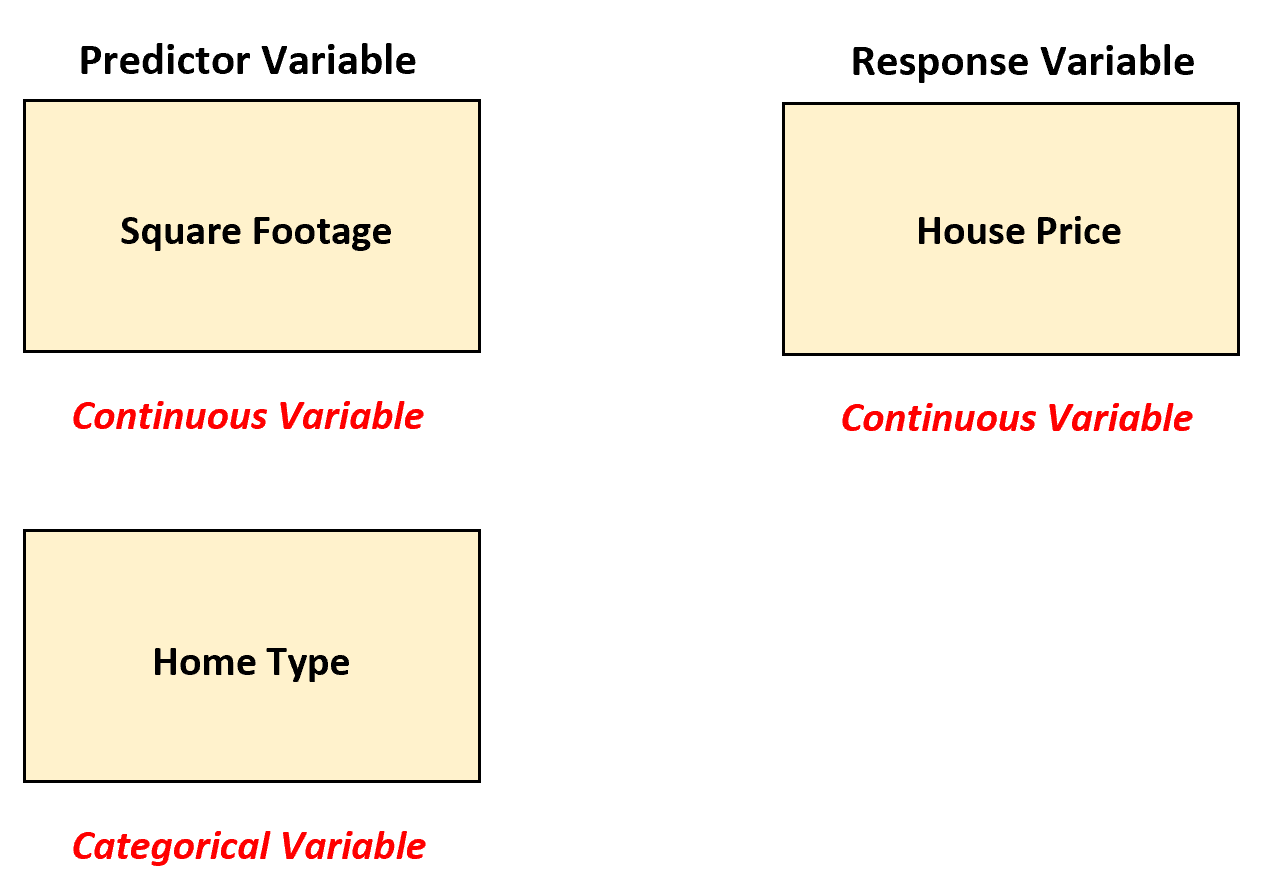
Der Immobilienmakler kann dann das folgende multiple lineare Regressionsmodell anpassen:
Immobilienpreis = β 0 + β 1 (Quadratfläche) + β 2 (Einfamilienhaus) + β 3 (Wohnung)
So würden wir die Modellkoeffizienten interpretieren:
- β 1 : Die durchschnittliche Änderung des Hauspreises, die mit einem zusätzlichen Quadratfuß einhergeht.
- β 2 : Der durchschnittliche Preisunterschied zwischen einem Einfamilienhaus und einem Stadthaus bei konstanter Quadratmeterzahl.
- β 3 : Durchschnittlicher Preisunterschied zwischen einem Einfamilienhaus und einer Wohnung bei konstanter Fläche.
Sehen Sie sich die folgenden Tutorials an, um zu erfahren, wie Sie Dummy-Variablen in verschiedenen Statistikprogrammen erstellen:
Zusätzliche Ressourcen
Die folgenden Tutorials bieten eine ausführliche Einführung in ANOVA-Modelle:
Die folgenden Tutorials bieten eine ausführliche Einführung in lineare Regressionsmodelle:
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen