Kumulierte häufigkeit

In diesem Artikel wird erklärt, was die kumulative Häufigkeit in der Statistik ist. So erfahren Sie, was die Summenhäufigkeit bedeutet, wie die Summenhäufigkeit anhand von Beispielen berechnet wird und schließlich, welche verschiedenen Arten der Summenhäufigkeit es gibt.

Was ist die kumulative Häufigkeit?

In der Statistik ist die kumulative Häufigkeit die kumulative Summe der Häufigkeiten. Das heißt, die kumulative Häufigkeit eines Werts ist gleich der Häufigkeit dieses Werts plus der Häufigkeit aller niedrigeren Werte.

Es gibt zwei Arten von kumulativen Häufigkeiten: kumulative absolute Häufigkeit und kumulative relative Häufigkeit. Nachfolgend sehen wir, wie jede Art der kumulativen Häufigkeit berechnet wird.

Bedenken Sie, dass Sie sich zunächst über das Konzept der Häufigkeit im Klaren sein müssen, um zu verstehen, was kumulative Häufigkeit in der Statistik bedeutet. Aus diesem Grund wird empfohlen, den folgenden Beitrag zu lesen, bevor Sie mit der Erklärung fortfahren:

So berechnen Sie die kumulative Häufigkeit

Die Schritte zur Berechnung der kumulativen Häufigkeit einer statistischen Stichprobe sind:

1. Erstellen Sie eine Tabelle mit allen verschiedenen Werten, die im Datensatz erscheinen, sortiert vom kleinsten zum größten.
2. Ermitteln Sie die absolute Häufigkeit jedes Werts.
3. Ermitteln Sie die kumulative Häufigkeit jedes Werts, die durch Addition der Häufigkeit des Werts selbst plus der Häufigkeit aller kleineren Werte berechnet wird.

Daher lautet die Formel zur Berechnung der kumulativen Häufigkeit:

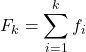
Gold:

• 

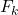
  ist die kumulative Häufigkeit des Werts

  

  .

• 

  ist die absolute Häufigkeit des Wertes

  

  .

Beachten Sie, dass diese Schritte zur Berechnung der kumulativen absoluten Häufigkeit dienen, es aber auch eine kumulative relative Häufigkeit gibt. Im Folgenden sehen wir den Unterschied zwischen diesen beiden Arten von akkumulierten Häufigkeiten und wie jeder Typ gefunden wird.

Arten von kumulativen Häufigkeiten

In der Statistik gibt es zwei Arten von Summenhäufigkeiten :

• Kumulierte absolute Häufigkeit : Dies ist die kumulative Summe der absoluten Häufigkeiten .
• Kumulierte relative Häufigkeit : Dies ist die kumulative Summe der relativen Häufigkeiten .

Unter Berücksichtigung der Definition jeder Art von akkumulierter Häufigkeit sehen Sie unten ein Beispiel dafür, wie jede Art ermittelt wird.

Kumulierte absolute Häufigkeit

Die kumulative absolute Häufigkeit wird durch das Symbol F _i dargestellt und wird durch Addition der absoluten Häufigkeiten von Werten berechnet, die gleich oder kleiner als der betreffende Wert sind. Als nächstes haben Sie ein konkretes Beispiel, in dem die kumulative absolute Häufigkeit eines statistischen Datensatzes berechnet wird.

• Die im Fach Statistik in einer Klasse mit 30 Schülern erzielten Noten lauten wie folgt. Wie groß ist die kumulative absolute Häufigkeit jeder Note?

Da alle Zahlen nur ganze Zahlen sein können, handelt es sich um eine diskrete Variable. Eine Gruppierung der Daten in Intervalle ist daher nicht erforderlich.

Um die kumulative absolute Häufigkeit zu bestimmen, müssen wir also zunächst die absolute Häufigkeit jedes Werts ermitteln, also die Häufigkeit, mit der jeder Wert in der statistischen Stichprobe vorkommt.

Da wir nun die absolute Häufigkeit jedes Werts kennen, können wir deren kumulative absolute Häufigkeit berechnen. Dazu haben wir zwei Möglichkeiten: Entweder wir addieren die absolute Häufigkeit des Wertes plus alle absoluten Häufigkeiten der kleinsten Werte, oder im Gegenteil, wir addieren die absolute Häufigkeit des Werts plus die kumulative absolute Häufigkeit der vorherigen Werte . Wert.

Kurz gesagt sieht die Tabelle mit der absoluten kumulativen Trainingshäufigkeit wie folgt aus:

Beachten Sie, dass die kumulierte absolute Häufigkeit des letzten Werts immer mit der Gesamtzahl der Daten übereinstimmt. Andernfalls liegt ein Fehler bei der Berechnung vor.

Kumulierte relative Häufigkeit

Die kumulative relative Häufigkeit wird durch das Symbol H _i dargestellt und durch Addition der relativen Häufigkeiten von Werten berechnet, die gleich oder kleiner als der betreffende Wert sind. Unten sehen Sie eine Übung, die mit denselben Daten wie die vorherige Aufgabe gelöst wurde und bei der die kumulative relative Häufigkeit bestimmt wird.

• Die in der Statistik in einer Klasse mit 30 Schülern erzielten Noten lauten wie folgt. Wie hoch ist die kumulative relative Häufigkeit jeder Note?

In diesem Fall ist die Variable diskret, da sie keinen Dezimalwert annehmen kann. Es ist also nicht nötig, die Daten nach Intervallen zu gruppieren, sondern wir können die Berechnungen direkt durchführen.

Also erstellen wir eine Häufigkeitstabelle und bestimmen die absolute Häufigkeit jedes einzelnen Wertes:

Als nächstes berechnen wir die relative Häufigkeit jedes Werts, die durch Division der absoluten Häufigkeit durch die Gesamtzahl der Beobachtungen (30) ermittelt wird.

Und sobald wir die absolute Häufigkeit und die relative Häufigkeit des Datensatzes berechnet haben, können wir die kumulative relative Häufigkeit ermitteln. Dazu müssen Sie die relative Häufigkeit des betreffenden Wertes plus alle vorherigen relativen Häufigkeiten oder, was auf dasselbe hinausläuft, die bisherige kumulierte relative Häufigkeit addieren:

Kurz gesagt, die Häufigkeitstabelle mit absoluter Häufigkeit, relativer Häufigkeit und kumulativer relativer Häufigkeit lautet wie folgt:

Beachten Sie, dass der letzte Wert der kumulativen relativen Häufigkeit immer 1 sein sollte. Wenn Sie eine andere Zahl erhalten, bedeutet dies, dass Sie bei den Berechnungen einen Fehler gemacht haben.