Warum sind statistiken wichtig? (10 gründe, warum statistiken wichtig sind!)

Der Bereich Statistik beschäftigt sich mit der Erhebung, Analyse, Interpretation und Darstellung von Daten.

Da Technologie in unserem täglichen Leben immer präsenter wird, werden mehr Daten generiert und gesammelt als je zuvor in der Geschichte der Menschheit.

Statistiken sind der Bereich, der uns helfen kann zu verstehen, wie wir diese Daten zur Ausführung der folgenden Aufgaben nutzen können:

• Verstehen Sie die Welt um uns herum besser.
• Treffen Sie Entscheidungen mithilfe von Daten.
• Machen Sie mithilfe von Daten Vorhersagen über die Zukunft.

In diesem Artikel teilen wir 10 Gründe, warum der Bereich Statistik im modernen Leben so wichtig ist.

Grund 1: Beschreibende Statistiken verwenden, um die Welt zu verstehen

Beschreibende Statistiken werden verwendet, um ein Stück Rohdaten zu beschreiben. Es gibt drei Haupttypen der deskriptiven Statistik:

• Zusammengefasste Statistiken
• Grafik
• die Tische

Jedes dieser Elemente kann uns helfen, vorhandene Daten besser zu verstehen.

Nehmen wir zum Beispiel an, wir haben einen Rohdatensatz, der die Testergebnisse von 10.000 Schülern in einer bestimmten Stadt zeigt. Wir können deskriptive Statistiken verwenden, um:

• Berechnen Sie das durchschnittliche Testergebnis und die Standardabweichung der Testergebnisse.
• Erstellen Sie ein Histogramm oder Boxplot, um die Verteilung der Testergebnisse zu visualisieren.
• Erstellen Sie eine Häufigkeitstabelle, um die Verteilung der Testergebnisse zu verstehen.

Durch die Verwendung deskriptiver Statistiken können wir die Testergebnisse der Schüler viel einfacher verstehen, als wenn wir nur die Rohdaten betrachten.

Grund 2: Vorsicht vor irreführenden Grafiken

In Zeitschriften, Medien, Online-Artikeln und Magazinen werden immer mehr Grafiken generiert. Leider können Diagramme oft irreführend sein, wenn Sie die zugrunde liegenden Daten nicht verstehen.

Angenommen, eine Zeitschrift veröffentlicht eine Studie, die eine negative Korrelation zwischen den GPA- und ACT-Ergebnissen von Studenten einer bestimmten Universität feststellt.

Dieser negative Zusammenhang tritt jedoch nur auf, weil Studierende mit einem hohen GPA- und ACT-Ergebnis eine Eliteuniversität besuchen können, während Studierende mit einem niedrigen GPA- und ACT-Ergebnis überhaupt nicht zugelassen werden.

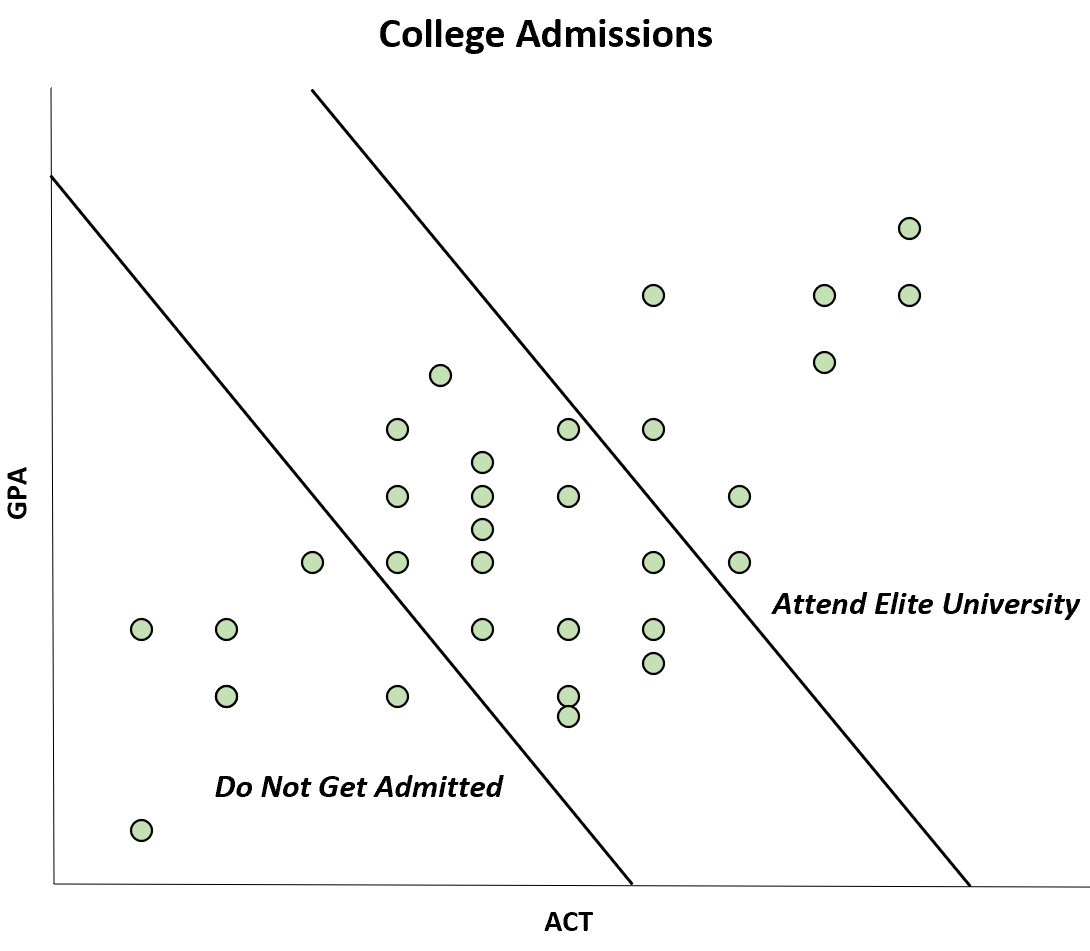
Obwohl die Korrelation zwischen ACT und GPA in der Bevölkerung positiv ist, scheint die Korrelation in der Stichprobe negativ zu sein.

Diese besondere Voreingenommenheit wird als Berkson-Voreingenommenheit bezeichnet. Wenn Sie sich dieser Voreingenommenheit bewusst sind, können Sie vermeiden, durch bestimmte Diagramme in die Irre geführt zu werden.

Grund 3: Seien Sie vorsichtig bei verwirrenden Variablen

Ein wichtiges Konzept, das Sie in der Statistik kennenlernen werden, ist das Konzept der verwirrenden Variablen .

Dies sind Variablen, die nicht berücksichtigt werden und die Ergebnisse eines Experiments verfälschen und zu unzuverlässigen Schlussfolgerungen führen können.

Angenommen, ein Forscher sammelt Daten über Eisverkäufe und Hai-Angriffe und stellt fest, dass die beiden Variablen stark korrelieren. Bedeutet das, dass gestiegene Eisverkäufe zu mehr Hai-Angriffen führen?

Es ist unwahrscheinlich. Die wahrscheinlichste Ursache ist die verwirrende Variable Temperatur . Wenn es draußen wärmer ist, kaufen mehr Menschen Eis und mehr Menschen gehen ans Meer.

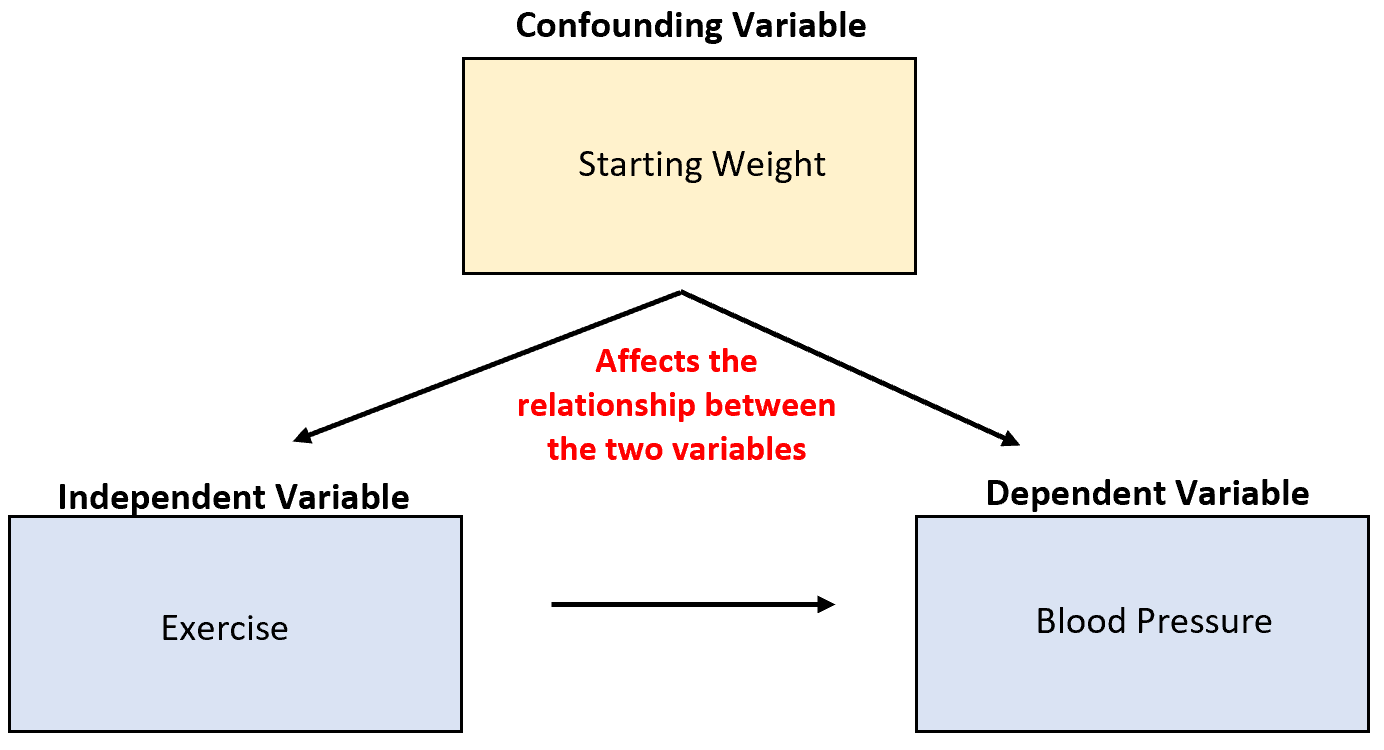
Grund 4: bessere Entscheidungen anhand von Wahrscheinlichkeiten treffen

Eines der wichtigsten Teilgebiete der Statistik ist die Wahrscheinlichkeitsrechnung . Es ist das Fachgebiet, das die Wahrscheinlichkeit des Eintretens von Ereignissen untersucht.

Wenn Sie über ein grundlegendes Verständnis der Wahrscheinlichkeit verfügen, können Sie in der realen Welt fundiertere Entscheidungen treffen.

Angenommen, ein Gymnasiast weiß, dass seine Chance, an einer bestimmten Universität angenommen zu werden, bei 10 % liegt. Mithilfe der Formel für die Wahrscheinlichkeit, „mindestens eins“ zu bestehen , kann dieser Student die Wahrscheinlichkeit ermitteln, dass er an mindestens einer Hochschule angenommen wird, an der er sich bewirbt, und kann die Anzahl der Hochschulen, an denen er sich bewirbt, je nach Ergebnis anpassen.

Grund 5: P-Werte in der Forschung verstehen

Ein weiteres wichtiges Konzept, das Sie in der Statistik kennenlernen werden, sind p-Werte .

Die klassische Definition eines p-Werts lautet:

Ein p-Wert ist die Wahrscheinlichkeit, eine Stichprobenstatistik zu beobachten, die mindestens so extrem ist wie Ihre Stichprobenstatistik, vorausgesetzt, die Nullhypothese ist wahr.

Angenommen, eine Fabrik gibt an, Reifen mit einem Durchschnittsgewicht von 200 Pfund herzustellen. Ein Prüfer geht davon aus, dass das tatsächliche Durchschnittsgewicht der in diesem Werk produzierten Reifen um 200 Pfund davon abweicht. Also führt er einen Hypothesentest durch und stellt fest, dass der p-Wert des Tests 0,04 beträgt.

So interpretieren Sie diesen p-Wert:

Wenn die Fabrik tatsächlich Reifen mit einem durchschnittlichen Gewicht von 200 Pfund herstellt, erzielen 4 % aller Audits aufgrund zufälliger Stichprobenfehler den in der Stichprobe beobachteten Effekt oder mehr. Dies zeigt uns, dass der Erhalt der vom Prüfer erhaltenen Beispieldaten recht selten wäre, wenn die Fabrik tatsächlich Reifen mit einem Durchschnittsgewicht von 200 Pfund produzierte.

Daher würde der Prüfer wahrscheinlich die Nullhypothese zurückweisen, dass das tatsächliche Durchschnittsgewicht der in diesem Werk hergestellten Reifen tatsächlich 200 Pfund beträgt.

Grund 6: Verstehen Sie den Zusammenhang

Ein weiteres wichtiges Konzept, das Sie in der Statistik kennenlernen werden, ist die Korrelation , die uns den linearen Zusammenhang zwischen zwei Variablen verrät.

Der Wert eines Korrelationskoeffizienten liegt immer zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Wenn Sie diese Werte verstehen, können Sie die Beziehung zwischen Variablen in der realen Welt verstehen.

Wenn beispielsweise die Korrelation zwischen Werbeausgaben und Einnahmen 0,87 beträgt, können Sie verstehen, dass zwischen den beiden Variablen ein starker positiver Zusammenhang besteht. Wenn Sie mehr Geld für Werbung ausgeben, können Sie mit einer vorhersehbaren Umsatzsteigerung rechnen.

Grund 7: Machen Sie Vorhersagen über die Zukunft

Ein weiterer wichtiger Grund, Statistiken zu lernen, ist das Verständnis grundlegender Regressionsmodelle wie:

• Einfache lineare Regression
• Multiple lineare Regression
• Logistische Regression

Mit jedem dieser Modelle können Sie Vorhersagen über den zukünftigen Wert einer Antwortvariablen basierend auf dem Wert bestimmter Prädiktorvariablen im Modell treffen.

Beispielsweise verwenden Unternehmen in der realen Welt ständig mehrere lineare Regressionsmodelle, wenn sie Prädiktorvariablen wie Alter, Einkommen, ethnische Zugehörigkeit usw. verwenden. um vorherzusagen, wie viele Kunden in ihren Geschäften Geld ausgeben werden.

Ebenso nutzen Logistikunternehmen prädiktive Variablen wie Gesamtnachfrage, Bevölkerungsgröße usw. um zukünftige Umsätze zu prognostizieren.

Unabhängig davon, in welchem Bereich Sie arbeiten, besteht eine gute Chance, dass Regressionsmodelle zur Vorhersage eines zukünftigen Phänomens verwendet werden.

Grund 8: Mögliche Verzerrungen in Studien verstehen

Ein weiterer Grund, sich mit Statistik zu befassen, besteht darin, sich der verschiedenen Arten von Verzerrungen bewusst zu sein, die in realen Studien auftreten können.

Hier sind einige Beispiele:

• Beobachten Sie Voreingenommenheit
• Voreingenommenheit bei der Selbstauswahl
• Referenzvoreingenommenheit
• Weggelassener variabler Bias
• Unterzählvoreingenommenheit
• Non-Response-Bias

Wenn Sie über ein grundlegendes Verständnis dieser Art von Voreingenommenheit verfügen, können Sie sie bei der Durchführung von Forschungsarbeiten vermeiden oder sich ihrer beim Lesen anderer Forschungsarbeiten oder Studien bewusst sein.

Grund 9: Verstehen Sie die Annahmen statistischer Tests

Viele statistische Tests basieren auf Annahmen über die zugrunde liegenden Daten, die untersucht werden.

Wenn Sie die Ergebnisse einer Studie lesen oder sogar eine eigene Studie durchführen, ist es wichtig zu verstehen, welche Annahmen getroffen werden müssen, damit die Ergebnisse zuverlässig sind.

In den folgenden Artikeln werden die Annahmen beschrieben, die in vielen häufig verwendeten statistischen Tests und Verfahren getroffen werden:

• Was ist die Annahme gleicher Varianz in der Statistik?
• Was ist die Normalitätsannahme in der Statistik?
• Was ist die Unabhängigkeitsannahme in der Statistik?

Grund 10: Um eine Überverallgemeinerung zu vermeiden

Ein weiterer Grund, Statistik zu studieren, besteht darin, das Konzept der Übergeneralisierung zu verstehen.

Dies liegt vor, wenn die an einer Studie teilnehmenden Personen nicht repräsentativ für die Gesamtbevölkerung sind und es daher unangemessen ist, die Ergebnisse einer Studie auf die Gesamtbevölkerung zu übertragen.

Nehmen wir zum Beispiel an, wir möchten wissen, wie viel Prozent der Schüler einer bestimmten Schule „Drama“ als ihr Lieblingsfilmgenre bevorzugen. Wenn die gesamte Schülerschaft eine Mischung aus 50 % Jungen und 50 % Mädchen ist, dann könnte eine Stichprobe, die aus 90 % Jungen und 10 % Mädchen besteht, zu verzerrten Ergebnissen führen, wenn deutlich weniger Jungen Theater als Lieblingsgenre bevorzugen.

Im Idealfall möchten wir, dass unsere Stichprobe einer „Miniversion“ unserer Grundgesamtheit ähnelt. Wenn also die gesamte Schülerschaft zu 50 % aus Mädchen und zu 50 % aus Jungen besteht, wäre unsere Stichprobe nicht repräsentativ, wenn sie 90 % Jungen und nur 10 % Mädchen umfassen würde.

Unabhängig davon, ob Sie Ihre eigene Umfrage durchführen oder die Ergebnisse einer Umfrage lesen, ist es wichtig zu verstehen, ob die Stichprobendaten für die Gesamtbevölkerung repräsentativ sind und ob die Umfrageergebnisse zuverlässig auf die Bevölkerung übertragen werden können.

Zusätzliche Ressourcen

Sehen Sie sich die folgenden Artikel an, um ein grundlegendes Verständnis der wichtigsten Konzepte der Einführungsstatistik zu erlangen:

Beschreibende oder inferenzielle Statistik
Bevölkerung vs. Probe
Statistiken vs. Parameter
Qualitative und quantitative Variablen
Messniveaus: nominal, ordinal, Intervall und Verhältnis