Warum ist die stichprobengröße wichtig? (erklärung & beispiele)
Die Stichprobengröße bezieht sich auf die Gesamtzahl der an einem Experiment oder einer Studie beteiligten Personen.
Die Stichprobengröße ist wichtig, da sie sich direkt auf die Präzision auswirkt, mit der wir Populationsparameter schätzen können.
Um zu verstehen, warum dies so ist, ist es hilfreich, ein grundlegendes Verständnis der Konfidenzintervalle zu haben.
Eine kurze Erklärung der Konfidenzintervalle
In der Statistik versuchen wir oft, Bevölkerungsparameter zu messen – Zahlen, die bestimmte Merkmale einer gesamten Bevölkerung beschreiben.
Beispielsweise könnten wir daran interessiert sein, die durchschnittliche Körpergröße aller Personen in einer bestimmten Stadt zu messen.
Allerdings ist es oft zu teuer und zeitaufwändig, Daten über jedes Individuum in einer Population zu sammeln. Daher nehmen wir normalerweise eine Zufallsstichprobe aus der Grundgesamtheit und nutzen die Stichprobendaten, um den Grundgesamtheitsparameter zu schätzen.
Beispielsweise könnten wir Daten über die Körpergröße von 100 zufällig ausgewählten Personen in der Stadt sammeln. Anschließend können wir die durchschnittliche Größe der Personen in der Stichprobe berechnen. Wir können jedoch nicht sicher sein, dass der Stichprobenmittelwert genau mit dem Populationsmittelwert übereinstimmt.
Um dieser Unsicherheit Rechnung zu tragen, können wir ein Konfidenzintervall erstellen. Ein Konfidenzintervall ist ein Wertebereich, der wahrscheinlich einen Populationsparameter mit einem bestimmten Konfidenzniveau enthält.
Die Formel zur Berechnung eines Konfidenzintervalls für einen Grundgesamtheitsmittelwert lautet:
Konfidenzintervall = x +/- z*(s/√ n )
Gold:
- x : Stichprobenmittel
- z: der gewählte z-Wert
- s: Stichprobenstandardabweichung
- n: Stichprobengröße
Der von Ihnen verwendete Z-Wert hängt vom gewählten Konfidenzniveau ab. Die folgende Tabelle zeigt den Z-Wert, der den häufigsten Konfidenzniveauoptionen entspricht:
| Ein Maß an Selbstvertrauen | z-Wert |
|---|---|
| 0,90 | 1.645 |
| 0,95 | 1,96 |
| 0,99 | 2,58 |
Die Beziehung zwischen Stichprobengröße und Konfidenzintervallen
Angenommen, wir möchten das Durchschnittsgewicht einer Schildkrötenpopulation schätzen. Wir sammeln eine Zufallsstichprobe von Schildkröten mit folgenden Informationen:
- Stichprobengröße n = 25
- Durchschnittliches Probengewicht x = 300
- Stichprobenstandardabweichung s = 18,5
So berechnen Sie das 90 %-Konfidenzintervall für das tatsächliche Durchschnittsgewicht der Bevölkerung:
90 %-Konfidenzintervall: 300 +/- 1,645*(18,5/√ 25 ) = [293,91, 306,09]
Wir sind zu 90 % sicher, dass das tatsächliche Durchschnittsgewicht der Schildkröten in der Population zwischen 293,91 und 306,09 Pfund liegt.
Nehmen wir nun an, dass wir statt 25 Schildkröten Daten über 50 Schildkröten sammeln.
So berechnen Sie das 90 %-Konfidenzintervall für das tatsächliche Durchschnittsgewicht der Bevölkerung:
90 %-Konfidenzintervall: 300 +/- 1,645*(18,5/√ 50 ) = [295,79, 304,30]
Beachten Sie, dass dieses Konfidenzintervall schmaler ist als das vorherige Konfidenzintervall. Das bedeutet, dass unsere Schätzung des wahren Durchschnittsgewichts der Schildkrötenpopulation genauer ist.
Nehmen wir nun an, wir sammeln Daten von 100 Schildkröten.
So berechnen Sie das 90 %-Konfidenzintervall für das tatsächliche Durchschnittsgewicht der Bevölkerung:
90 %-Konfidenzintervall: 300 +/- 1,645*(18,5/√ 100 ) = [296,96, 303,04]
Beachten Sie, dass dieses Konfidenzintervall noch enger ist als das vorherige Konfidenzintervall.
Die folgende Tabelle fasst die einzelnen Konfidenzintervallbreiten zusammen:
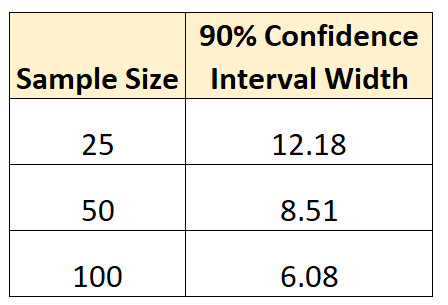
Hier ist die Quintessenz: Je größer die Stichprobengröße, desto genauer können wir einen Populationsparameter schätzen .
Zusätzliche Ressourcen
Die folgenden Tutorials bieten weitere hilfreiche Erklärungen zu Konfidenzintervallen und Stichprobengröße.
Eine Einführung in Konfidenzintervalle
4 Beispiele für Konfidenzintervalle im wirklichen Leben
Bevölkerung vs. Beispiel: Was ist der Unterschied?