4 beispiele für die verwendung von chi-quadrat-tests im wirklichen leben
In der Statistik gibt es zwei verschiedene Arten von Chi-Quadrat-Tests:
1. Chi-Quadrat-Anpassungstest – Wird verwendet, um zu bestimmen, ob eine kategoriale Variable einer hypothetischen Verteilung folgt oder nicht.
2.Der Chi-Quadrat-Unabhängigkeitstest – Wird verwendet, um festzustellen, ob zwischen zwei kategorialen Variablen ein signifikanter Zusammenhang besteht oder nicht.
In diesem Artikel teilen wir mehrere Beispiele dafür, wie jede dieser Arten von Chi-Quadrat-Tests in realen Situationen verwendet wird.
Beispiel 1: Chi-Quadrat-Anpassungstest
Angenommen, ein Ladenbesitzer behauptet, dass an jedem Tag der Woche gleich viele Kunden in sein Geschäft kommen.
Um diese Hypothese zu testen, erfasst er die Anzahl der Kunden, die in einer bestimmten Woche in den Laden kommen, und stellt Folgendes fest:
- Montag: 50 Kunden
- Dienstag: 60 Kunden
- Mittwoch: 40 Kunden
- Donnerstag: 47 Kunden
- Freitag: 53 Kunden
Mithilfe eines Chi-Quadrat-Anpassungstests kann er ermitteln, ob die Verteilung der Kunden, die jeden Tag kommen, mit seiner Verteilungshypothese übereinstimmt.
Mithilfe des Chi-Quadrat-Anpassungstestrechners kann er erkennen, dass der p-Wert des Tests 0,359 beträgt.
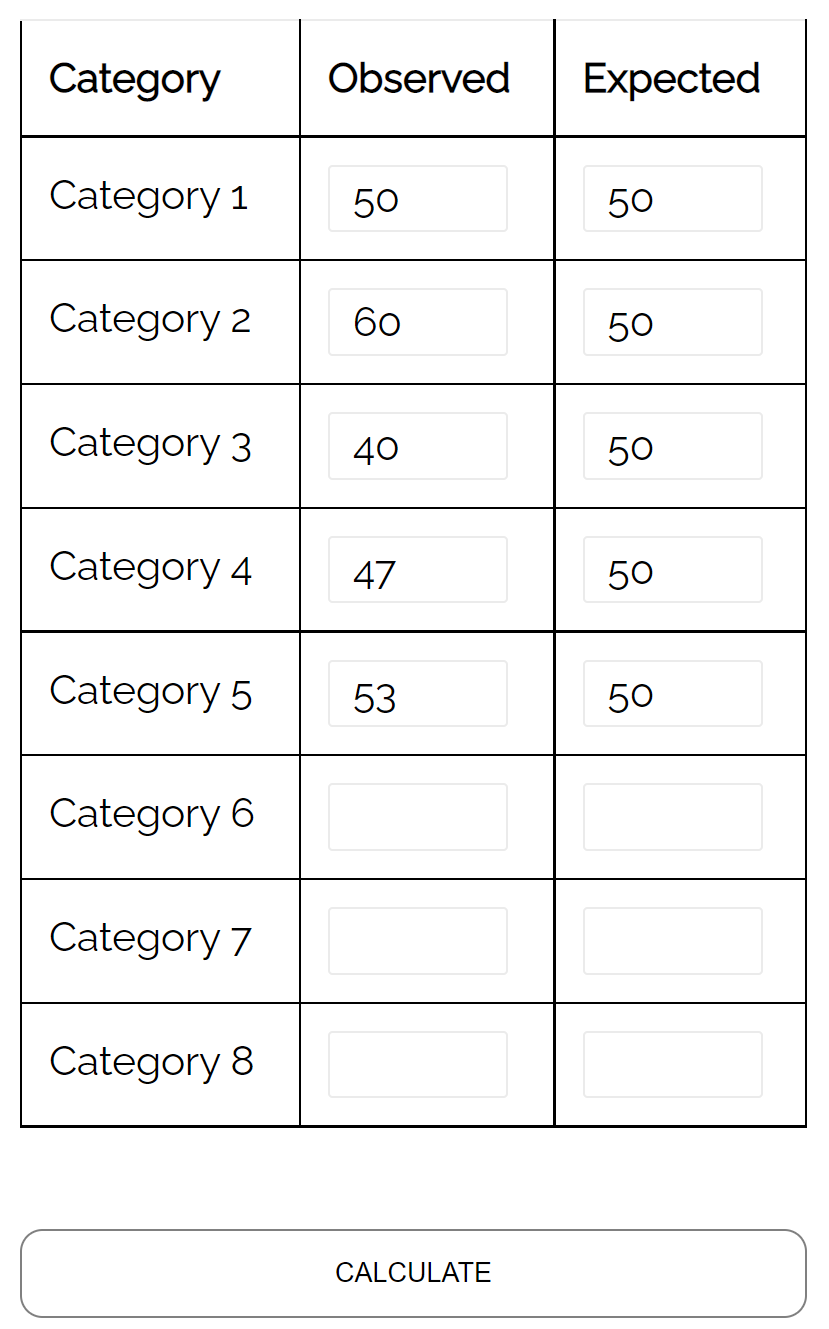

Da dieser p-Wert nicht weniger als 0,05 beträgt, gibt es keine ausreichenden Beweise dafür, dass die tatsächliche Kundenverteilung von der vom Ladenbesitzer behaupteten abweicht.
Beispiel 2: Chi-Quadrat-Anpassungstest
Angenommen, ein Biologe behauptet, dass jede Woche die gleiche Anzahl von vier verschiedenen Hirscharten in ein bestimmtes Waldgebiet eindringt.
Um diese Hypothese zu testen, zeichnet sie die Anzahl jeder Hirschart auf, die im Laufe einer Woche in das Waldgebiet gelangt:
- Art Nr. 1: 22
- Art Nr. 2: 20
- Art Nr. 3: 23
- Art Nr. 4: 35
Mithilfe eines Chi-Quadrat-Anpassungstests kann sie feststellen, ob die Verteilung der Hirscharten, die jede Woche in das Waldgebiet des Waldes eindringen, mit ihrer hypothetischen Verteilung übereinstimmt.
Mithilfe des Chi-Quadrat-Anpassungstestrechners kann sie erkennen, dass der p-Wert für den Test 0,137 beträgt.
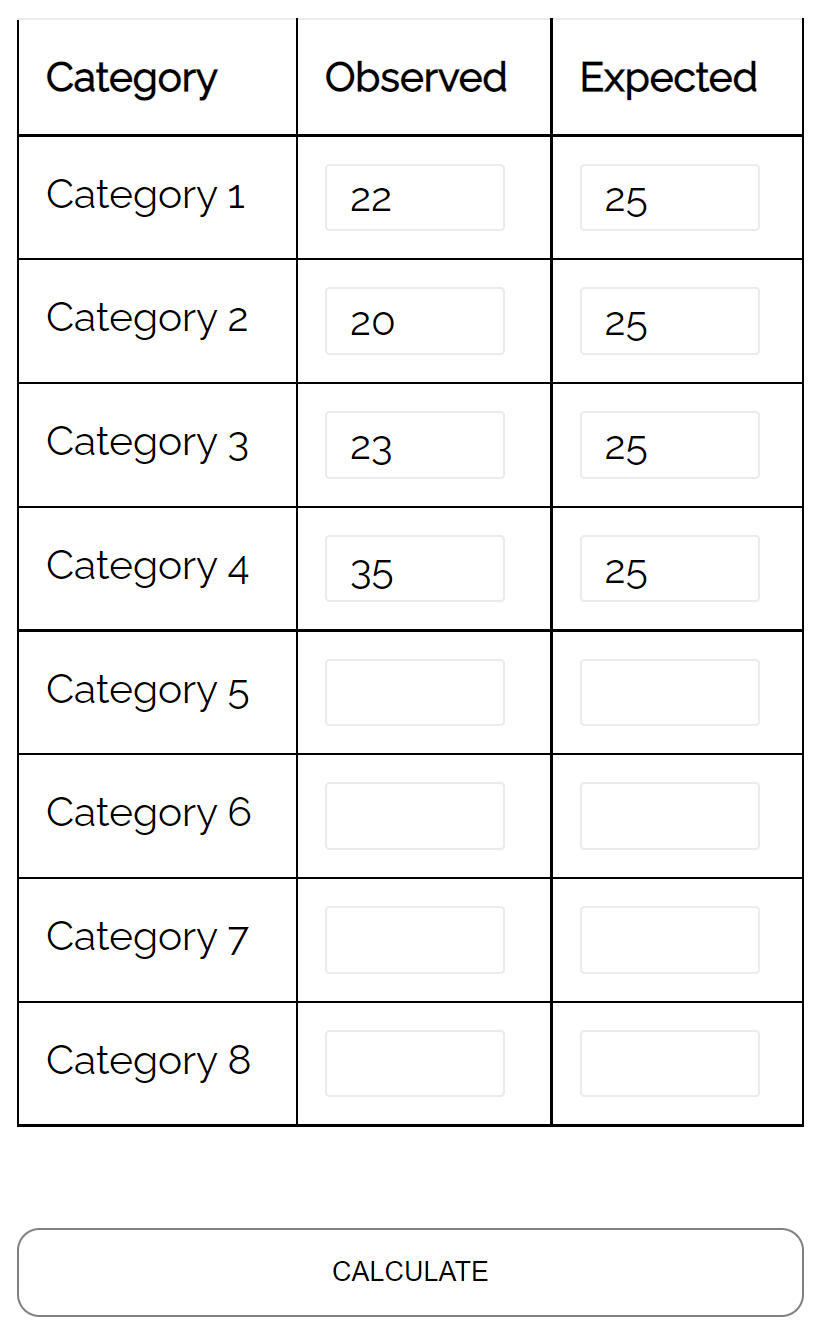
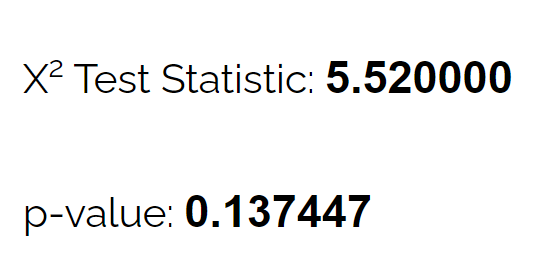
Da dieser p-Wert nicht weniger als 0,05 beträgt, gibt es keine ausreichenden Beweise dafür, dass die tatsächliche Verbreitung der Hirsche von der vom Biologen behaupteten abweicht.
Beispiel 3: Chi-Quadrat-Unabhängigkeitstest
Angenommen, ein politischer Entscheidungsträger in einer bestimmten Stadt möchte wissen, ob das Geschlecht mit der Präferenz einer politischen Partei zusammenhängt.
Er beschließt, eine einfache Zufallsstichprobe von 500 Wählern zu ziehen und sie nach ihrer Präferenz für eine politische Partei zu befragen. Die folgende Tabelle stellt die Ergebnisse der Umfrage dar:
| Republikaner | Demokrat | Unabhängig | Gesamt | |
| Männlich | 120 | 90 | 40 | 250 |
| Weiblich | 110 | 95 | 45 | 250 |
| Gesamt | 230 | 185 | 85 | 500 |
Mithilfe eines Chi-Quadrat-Unabhängigkeitstests kann ermittelt werden, ob zwischen den beiden Variablen ein statistisch signifikanter Zusammenhang besteht.
Mithilfe des Chi-Quadrat-Unabhängigkeitstest-Rechners kann er erkennen, dass der p-Wert des Tests 0,649 beträgt.
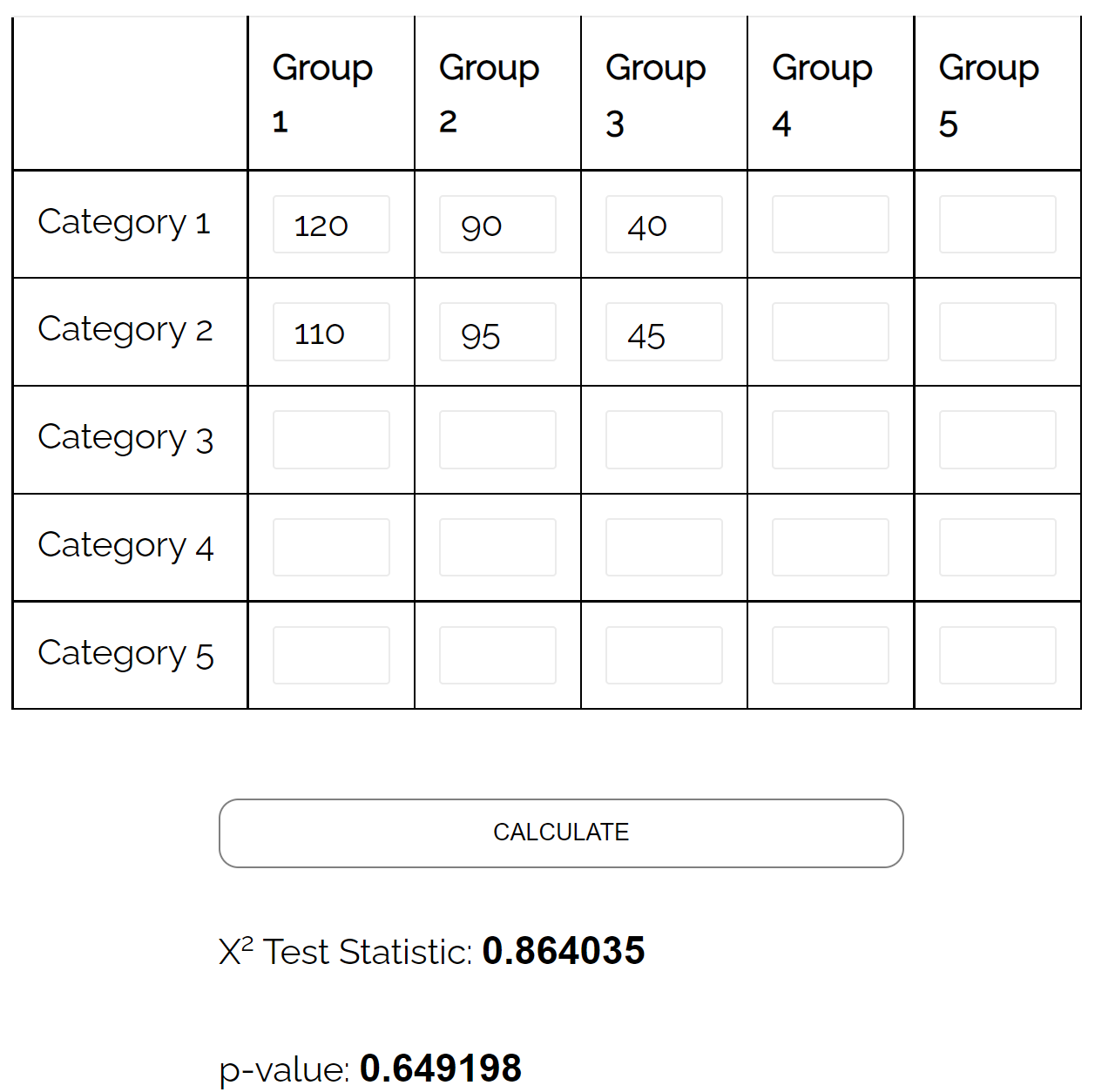
Da der p-Wert nicht weniger als 0,05 beträgt, gibt es keine ausreichenden Belege dafür, dass ein Zusammenhang zwischen Geschlecht und Parteipräferenz besteht.
Beispiel 4: Chi-Quadrat-Unabhängigkeitstest
Angenommen, ein Forscher möchte wissen, ob der Familienstand mit dem Bildungsniveau zusammenhängt.
Er beschließt, eine einfache Zufallsstichprobe von 300 Personen zu ziehen und kommt zu folgenden Ergebnissen:
| Weiterführende Schule | Junggesellen | Master oder höher | Gesamt | |
| Verheiratet | 20 | 100 | 35 | 155 |
| Bachelor | 50 | 80 | 15 | 145 |
| Gesamt | 70 | 180 | 50 | 300 |
Mithilfe eines Chi-Quadrat-Unabhängigkeitstests kann festgestellt werden, ob zwischen den beiden Variablen ein statistisch signifikanter Zusammenhang besteht.
Mithilfe des Chi-Quadrat-Unabhängigkeitstest-Rechners kann er erkennen, dass der p-Wert des Tests 0,000011 beträgt.
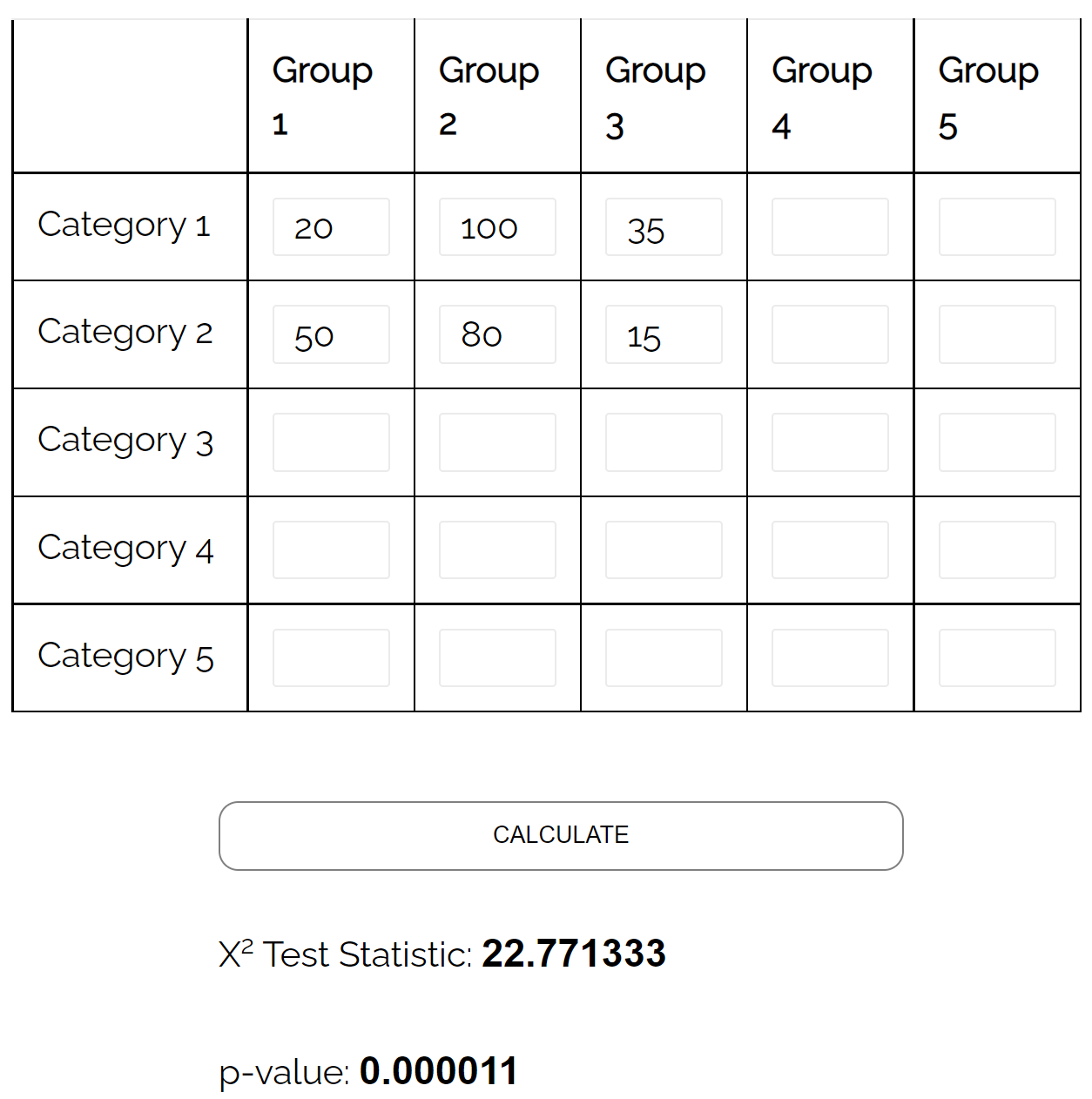
Da der p-Wert unter 0,05 liegt, gibt es genügend Belege dafür, dass ein Zusammenhang zwischen Familienstand und Bildungsniveau besteht.
Zusätzliche Ressourcen
Die folgenden Tutorials bieten eine Einführung in die verschiedenen Arten von Chi-Quadrat-Tests:
Die folgenden Tutorials erklären den Unterschied zwischen Chi-Quadrat-Tests und anderen statistischen Tests: