Benfords gesetz
Dieser Artikel erklärt, was Benfords Gesetz ist. Darüber hinaus erfahren Sie, wie das Benfordsche Gesetz entdeckt wurde und welche Anwendungsmöglichkeiten dieses statistische Gesetz bietet.
Was ist Benfords Gesetz?
Das Benfordsche Gesetz , auch Gesetz der ersten Ziffer genannt, ist ein statistisches Gesetz, das besagt, dass die Wahrscheinlichkeit, dass die erste Ziffer einer Datenmenge 1 ist, größer ist als die Wahrscheinlichkeit, dass es sich um eine andere Zahl handelt.
Mit anderen Worten besagt das Benfordsche Gesetz, dass in einem Satz numerischer Daten, die im wirklichen Leben existieren, die Zahl 1 die am häufigsten wiederholte Zahl als erste Ziffer der Daten ist.
Darüber hinaus gilt: Je höher die Zahl, desto unwahrscheinlicher ist es, dass man auf dem ersten Platz landet. Daher ist die erste Zahl wahrscheinlicher eine 1 als eine 2, aber 2 ist wahrscheinlicher als 3, 3 ist wahrscheinlicher als 4 und so weiter.
Benfords Gesetz verdankt seinen Namen dem Amerikaner Frank Benford. Obwohl er sie nicht erfunden hat, hat Benford diese statistische Regel populär gemacht. Unten sehen wir den Ursprung des Benford-Gesetzes.
Benfords Gesetzesformel
Das Benfordsche Gesetz besagt, dass die Wahrscheinlichkeit, dass die erste Ziffer eine bestimmte Zahl ist, gleich dem Logarithmus von eins plus eins über dieser Zahl ist.
Die Formel für das Benfordsche Gesetz lautet daher wie folgt:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
Daher können wir aus der Formel des Benford-Gesetzes die Wahrscheinlichkeit für jede Zahl ableiten, dass es sich um die erste Ziffer eines Datenelements handelt. In der folgenden Tabelle sehen Sie die Prozentsätze aller Wahrscheinlichkeiten:
| Figur | Wahrscheinlichkeit, dass sei die erste Zahl |
|---|---|
| 1 | 30,1 % |
| 2 | 17,6 % |
| 3 | 12,5 % |
| 4 | 9,7 % |
| 5 | 7,9 % |
| 6 | 6,7 % |
| 7 | 5,8 % |
| 8 | 5,1 % |
| 9 | 4,6 % |
Zusätzlich sehen Sie unten ein Histogramm, in dem alle Wahrscheinlichkeiten des Benfordschen Gesetzes grafisch dargestellt sind:
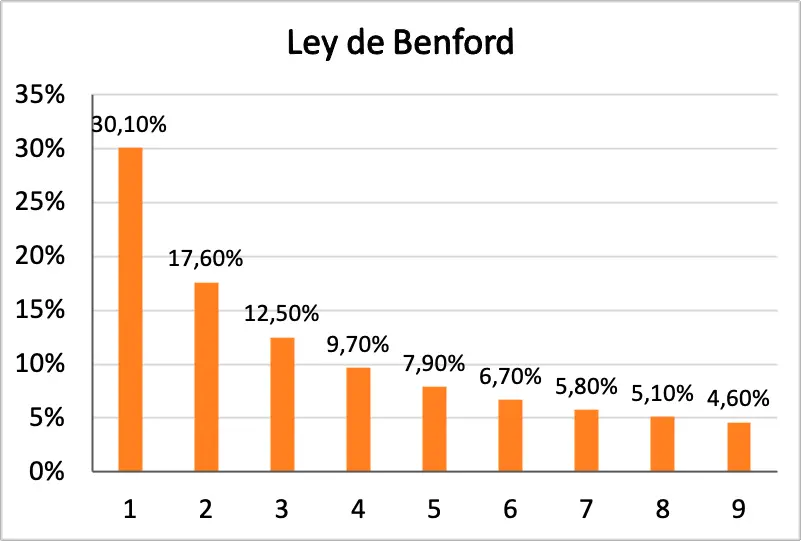
Geschichte des Benfordschen Gesetzes
Im Jahr 1881 leitete der Mathematiker Simon Newcomb das Benfordsche Gesetz ab, als er entdeckte, dass die ersten Seiten von Logarithmentabellen wesentlich häufiger verwendet wurden als die letzten Seiten. Das bedeutet, dass die ersten Ziffern von Zahlen nicht gleich wahrscheinlich sind, sondern dass 1 häufiger als 2, 2 häufiger als 3 und so weiter bis 9 vorkommt.
Allerdings hinterließ Newcomb keine statistischen Beweise dafür, dass diese Regel befolgt wurde, er zog lediglich eine Ableitung aus der Abnutzung der logarithmischen Tabellen.
Später, genauer gesagt im Jahr 1938, machte der Physiker Frank Benford die gleiche Beobachtung und führte auch ein Experiment durch, um sie empirisch zu überprüfen. Anhand eines statistischen Datensatzes mit 20.229 Werten aus 20 verschiedenen Stichproben führte er eine Studie zur ersten Ziffer jedes Datentyps durch. Basierend auf den Ergebnissen zeigte er, dass das Benfordsche Gesetz erfüllt war, und leitete die Formel ab, die es ihm ermöglichte, die Wahrscheinlichkeit zu berechnen, dass die erste Ziffer eine bestimmte Zahl ist (wir haben diese Formel oben gesehen).
Kurz gesagt: Obwohl das Benfordsche Gesetz zuerst von Simon Newcomb entdeckt wurde, ist es nach Frank Benford benannt, weil er derjenige war, der dieses statistische Gesetz bestätigt hat.
Anwendungen des Benfordschen Gesetzes
Das Benfordsche Gesetz ist ein statistisches Gesetz, das in sehr unterschiedlichen Bereichen Anwendung findet. Beispielsweise wird das Benfordsche Gesetz häufig in der Wirtschaft, Biologie und sogar in der Politik verwendet.
In den Wirtschaftswissenschaften wird das Benfordsche Gesetz häufig zur Erkennung von Datenmanipulationen verwendet, denn wenn ein Datensatz nicht dem Benfordschen Gesetz entspricht, deutet dies darauf hin, dass die Daten manipuliert wurden. Dieses Gesetz dient beispielsweise der Aufdeckung möglicher Fälle von Steuerbetrug.
Es ist zu beachten, dass das Benfordsche Gesetz nicht zum Nachweis der Wahrheit zufälliger Phänomene verwendet wird, da die Ergebnisse gleich wahrscheinlich sind. Daher kann die Benford-Regel nicht zur Überprüfung von Lotterieergebnissen verwendet werden.
Andererseits kann das Benfordsche Gesetz in der Genetik verwendet werden, um Unterschiede in der Genomlänge zwischen verschiedenen Arten von Organismen zu analysieren.
Schließlich wurden auch Versuche unternommen, Wahlbetrug durch Anwendung des Benford-Gesetzes aufzudecken, obwohl dessen Nützlichkeit in diesem Fall in Frage gestellt wurde.