Negative binomialverteilung

Von Dr. Benjamin Anderson August 3, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel wird erklärt, was die negative Binomialverteilung ist und wofür sie verwendet wird. Außerdem finden Sie die Formel für die negative Binomialverteilung, ein konkretes Beispiel und die Eigenschaften dieser Art von Wahrscheinlichkeitsverteilung. Schließlich können Sie mit einem Online-Rechner jede negative Binomialverteilungswahrscheinlichkeit berechnen.

Was ist die negative Binomialverteilung?

Die negative Binomialverteilung ist eine Wahrscheinlichkeitsverteilung, die die Anzahl der Bernoulli-Versuche beschreibt, die erforderlich sind, um eine bestimmte Anzahl positiver Ergebnisse zu erhalten.

Daher weist eine negative Binomialverteilung zwei charakteristische Parameter auf: r ist die Anzahl der gewünschten erfolgreichen Ergebnisse und p ist die Erfolgswahrscheinlichkeit für jedes durchgeführte Bernoulli-Experiment.

$X\sim \text{BN}(r,p)$

Denken Sie daran, dass ein Bernoulli-Test ein Experiment ist, das zwei mögliche Ergebnisse hat: „Erfolg“ und „Misserfolg“. Wenn also die Wahrscheinlichkeit des „Erfolgs“ p ist, ist die Wahrscheinlichkeit des „Misserfolgs“ q=1-p .

Somit definiert eine negative Binomialverteilung einen Prozess, bei dem so viele Bernoulli-Versuche durchgeführt werden, wie nötig sind, um positive Ergebnisse zu erhalten. Darüber hinaus sind alle diese Bernoulli-Versuche unabhängig und haben eine konstante Erfolgswahrscheinlichkeit .

Beispielsweise gibt eine Zufallsvariable, die einer negativen Binomialverteilung folgt, an, wie oft ein Würfel gewürfelt werden muss, bis die Zahl 6 dreimal gewürfelt wird.

Der Unterschied zwischen einer negativen Binomialverteilung und einer Binomialverteilung besteht darin, dass die negative Binomialverteilung zählt, wie oft es dauert, bis eine bestimmte Anzahl erfolgreicher Ergebnisse erzielt wird, während die Binomialverteilung die Anzahl erfolgreicher Fälle in einer Reihe von Bernoulli-Tests zählt.

➤ Siehe: Was ist die Binomialverteilung?

Negative Binomialverteilungsformel

Bei gegebenen Parametern r, p, x wird die Wahrscheinlichkeit einer negativen Binomialverteilung berechnet, indem die kombinatorische Zahl von x-1 in xr mit (1-p) ^xr mit p ^r multipliziert wird.

Die Formel zur Berechnung einer negativen Binomialverteilungswahrscheinlichkeit lautet also:

👉 Mit dem Rechner unten können Sie die Wahrscheinlichkeit einer Variablen berechnen, die der negativen Binomialverteilung folgt.

Übung zur negativen Binomialverteilung gelöst

Wie groß ist die Wahrscheinlichkeit, dass eine Münze, wenn man sie acht Mal wirft, beim achten Mal ein viertes Mal „Kopf“ ergibt?

Zuerst müssen wir die Wahrscheinlichkeit berechnen, beim Münzwurf „Kopf“ zu bekommen. In diesem Fall haben wir nur ein positives Ergebnis (Kopf) von zwei möglichen Ergebnissen (Kopf und Zahl), daher ist die Erfolgswahrscheinlichkeit:

$p=\cfrac{1}{2}=0,5$

Somit folgt die Zufallsvariable in diesem Problem einer negativen Binomialverteilung mit r=4 und p=0,5. Daher verwenden wir die negative Binomialverteilungsformel, um die Wahrscheinlichkeit zu berechnen, die die Übung von uns verlangt.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

Merkmale der negativen Binomialverteilung

Nachfolgend sind die wichtigsten Merkmale der negativen Binomialverteilung aufgeführt.

Die negative Binomialverteilung wird durch zwei charakteristische Parameter definiert: r ist die Anzahl der gewünschten erfolgreichen Ergebnisse und p ist die Erfolgswahrscheinlichkeit für jedes durchgeführte Bernoulli-Experiment.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

Die Varianz einer negativen Binomialverteilung ist gleich r multipliziert mit (1-p) dividiert durch p ² .

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

Wenn der Parameter r größer als 1 ist, kann der Modus einer negativen Binomialverteilung mit der folgenden Formel berechnet werden:

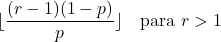
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=“Rendered by QuickLaTeX.com“ height=“42″ width=“221″ style=“vertical-align: -16px;“></p> </p> <ul> <li> Die Massenfunktion, die es ermöglicht, eine Wahrscheinlichkeit einer negativen Binomialverteilung zu bestimmen, lautet wie folgt:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

Der Schiefekoeffizient einer negativen Binomialverteilung wird mit dem folgenden Ausdruck berechnet:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

Die Kurtosis einer negativen Binomialverteilung kann mit der folgenden Formel ermittelt werden:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

Wenn der Parameter r gleich 1 ist, liegt ein Fall einer geometrischen Verteilung vor.

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Rechner für negative Binomialverteilung

Geben Sie die Werte der Parameter r, p, x in den folgenden Rechner ein, um die Wahrscheinlichkeit zu berechnen. Sie müssen Zahlen mit dem Punkt als Dezimaltrennzeichen eingeben, zum Beispiel 0,50.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen