Binomialverteilung

Von Dr. Benjamin Anderson August 3, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel wird erklärt, was die Binomialverteilung in der Statistik ist und wofür sie verwendet wird. Sie finden daher die Definition der Binomialverteilung, Beispiele für Binomialverteilungen und die Eigenschaften dieser Art von Wahrscheinlichkeitsverteilung. Darüber hinaus können Sie mit einem Online-Rechner jede beliebige Wahrscheinlichkeit der Binomialverteilung berechnen.

Was ist die Binomialverteilung?

Die Binomialverteilung ist eine Wahrscheinlichkeitsverteilung, die die Anzahl der Erfolge bei der Durchführung einer Reihe unabhängiger, dichotomer Experimente mit konstanter Erfolgswahrscheinlichkeit zählt.

Mit anderen Worten: Die Binomialverteilung ist eine Verteilung, die die Anzahl erfolgreicher Ergebnisse einer Folge von Bernoulli-Versuchen beschreibt.

Denken Sie daran, dass ein Bernoulli-Test ein Experiment ist, das zwei mögliche Ergebnisse hat: „Erfolg“ und „Misserfolg“. Wenn also die Wahrscheinlichkeit des „Erfolgs“ p ist, beträgt die Wahrscheinlichkeit des „Misserfolgs“ q=1-p .

Im Allgemeinen wird die Gesamtzahl der durchgeführten Experimente mit dem Parameter n definiert, während p die Erfolgswahrscheinlichkeit jedes Experiments ist. Somit wird eine Zufallsvariable, die einer Binomialverteilung folgt, wie folgt geschrieben:

$X\sim\text{Bin}(n,p)$

Beachten Sie, dass in einer Binomialverteilung genau dasselbe Experiment n -mal wiederholt wird und die Experimente unabhängig voneinander sind, sodass die Erfolgswahrscheinlichkeit jedes Experiments gleich ist (p) .

Die Binomialverteilung kann auch Binomialverteilung genannt werden.

Beispiele für Binomialverteilungen

Sobald wir die Definition der Binomialverteilung kennengelernt haben, werden wir zum besseren Verständnis des Konzepts mehrere Beispiele für Variablen sehen, die diesem Verteilungstyp folgen.

Anzahl der Fälle, in denen „Kopf“ erscheint, wenn eine Münze 25 Mal geworfen wird.
Anzahl der Schüsse eines Basketballspielers, wenn er 60 Mal von derselben Stelle aus auf den Korb schießt.
Wie oft wir die Zahl 6 erhalten, wenn wir 30 Mal würfeln.
Anzahl der bestandenen Prüfungen von insgesamt 50 Studierenden.
Anzahl fehlerhafter Einheiten in einer Stichprobe von 100 Produkten.

Binomialverteilungsformel

Bei gegebenen Parametern x, n, p ist die Wahrscheinlichkeitsfunktion der Binomialverteilung als die kombinatorische Zahl von n in x mal p ^x mal (1-p) ^nx definiert.

Daher lautet die Formel zur Berechnung der Wahrscheinlichkeit einer Binomialverteilung :

👉 Mit dem Rechner unten können Sie die Wahrscheinlichkeit einer Variablen berechnen, die der Binomialverteilung folgt.

Andererseits wird die kumulative Wahrscheinlichkeit der Binomialverteilung berechnet, indem die Wahrscheinlichkeiten der Anzahl der betreffenden Erfolgsfälle und aller vorherigen Wahrscheinlichkeiten addiert werden. Die Formel zur Berechnung der kumulativen Wahrscheinlichkeit einer Binomialverteilung lautet also:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Übung zur Binomialverteilung gelöst

Wir werfen eine Münze 10 Mal. Wie hoch ist die Wahrscheinlichkeit, dass wir 6 mal Kopf bekommen?

Die Variable in diesem Problem folgt einer Binomialverteilung, da alle Starts unabhängig voneinander sind und auch die gleiche Erfolgswahrscheinlichkeit haben.

Konkret beträgt die Erfolgswahrscheinlichkeit 50 %, da nur eines der beiden möglichen Ergebnisse als Erfolg gewertet wird.

$p=\cfrac{1}{2}=0,5$

Daher ist die Verteilung für diese Übung eine Binomialverteilung mit insgesamt 10 Experimenten und einer Wahrscheinlichkeit von 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Um also die Wahrscheinlichkeit zu bestimmen, sechs Köpfe zu bekommen, müssen wir die Binomialverteilungsformel anwenden.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Die Wahrscheinlichkeit, durch zehnmaliges Werfen einer Münze genau sechs Köpfe zu bekommen, beträgt also 20,51 %.

Merkmale der Binomialverteilung

Die Binomialverteilung weist folgende Merkmale auf:

Die Binomialverteilung wird mit zwei Parametern definiert: n ist die Gesamtzahl der Bernoulli-Experimente und p ist andererseits die Erfolgswahrscheinlichkeit jedes Bernoulli-Experiments.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

Der Mittelwert einer Binomialverteilung ist gleich dem Produkt aus der Gesamtzahl der Experimente multipliziert mit der Erfolgswahrscheinlichkeit jedes Experiments. Um den Mittelwert einer Binomialverteilung zu berechnen, muss man daher n mit p multiplizieren.

$E[X]=n\cdot p$

Die Varianz einer Binomialverteilung entspricht der Gesamtzahl der Versuche multipliziert mit der Erfolgswahrscheinlichkeit und der Misserfolgswahrscheinlichkeit.

$Var(X)=n\cdot p\cdot (1-p)$

Die Formel für die Wahrscheinlichkeitsfunktion der Binomialverteilung lautet wie folgt:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Ebenso lautet die Formel für die kumulative Verteilungsfunktion der Binomialverteilung:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Die Summe zweier unabhängiger Binomialverteilungen mit derselben Wahrscheinlichkeit entspricht einer Binomialverteilung mit demselben Wahrscheinlichkeitswert p und n als Summe der Gesamtzahl der Versuche der beiden Verteilungen.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

Die Bernoulli-Verteilung ist ein Sonderfall der Binomialverteilung, bei der n=1 ist , also nur ein Experiment durchgeführt wird.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Wenn _X 1 , _X ₂ ,…, X _k unabhängige Zufallsvariablen sind, so dass

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

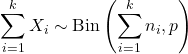
Binomialverteilungsrechner

Geben Sie die Werte der Parameter p, n und x der Binomialverteilung in den folgenden Rechner ein, um die Wahrscheinlichkeit zu berechnen. Sie müssen die Wahrscheinlichkeit auswählen, die Sie berechnen möchten, und die Zahlen mit dem Punkt als Dezimaltrennzeichen eingeben, zum Beispiel 0,1667.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen