Bedeutet kausalität korrelation? (3 beispiele)

Es ist bekannt, dass Korrelation keine Kausalität bedeutet .

Als einfaches Beispiel: Wenn wir jedes Jahr Daten über die Gesamtzahl der High-School-Absolventen und den gesamten Pizzakonsum in den Vereinigten Staaten sammeln würden, würden wir feststellen, dass die beiden Variablen stark korrelieren:

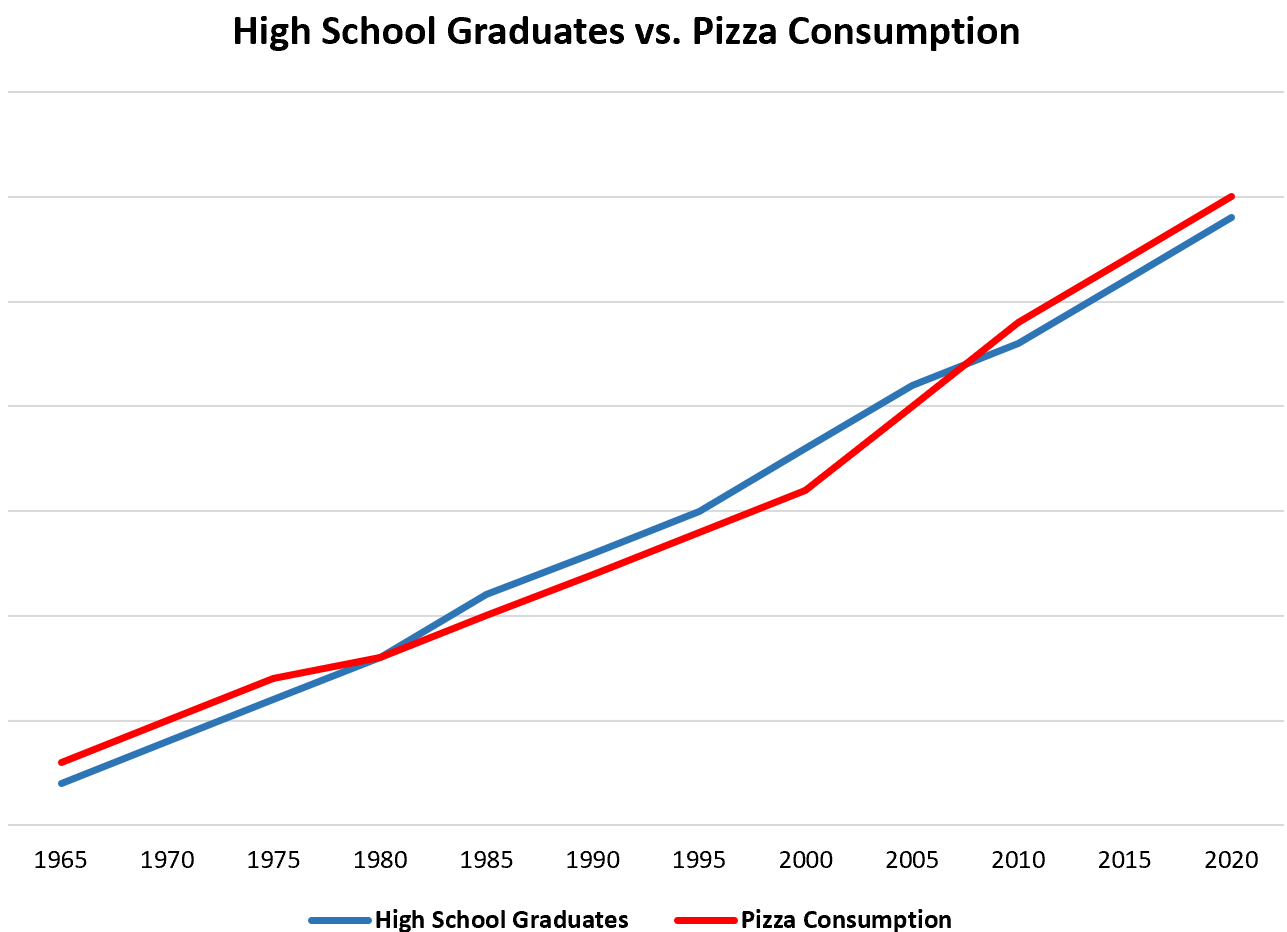
Dies bedeutet nicht, dass die steigende Zahl der Abiturienten zu einem Anstieg des Pizzakonsums führt .

Die wahrscheinlichste Erklärung ist, dass die US-Bevölkerung im Laufe der Zeit gewachsen ist, was bedeutet, dass die Zahl der Menschen mit einem High-School-Abschluss und die Gesamtmenge der konsumierten Pizza mit zunehmender Bevölkerung zunimmt.

Aber was ist mit der gegenteiligen Aussage: Bedeutet Kausalität Korrelation?

Wenn eine Variable eine andere Variable verursacht, bedeutet das dann zwangsläufig, dass die beiden Variablen korrelieren?

Die kurze Antwort: Nein.

Die folgenden Beispiele zeigen, warum.

Beispiel 1: Quadratische Beziehung

Angenommen, eine Variable X bewirkt, dass die Variable Y einen Wert gleich X ² annimmt.

Zum Beispiel:

• Wenn X = -10, dann Y = -10 ² = 100
• Wenn X = 0, dann ist Y = 0 ² = 0
• Wenn X = 10, dann ist Y = 10 ² = 100

Und so weiter.

Wenn wir die Beziehung zwischen X und Y darstellen, würde das so aussehen:

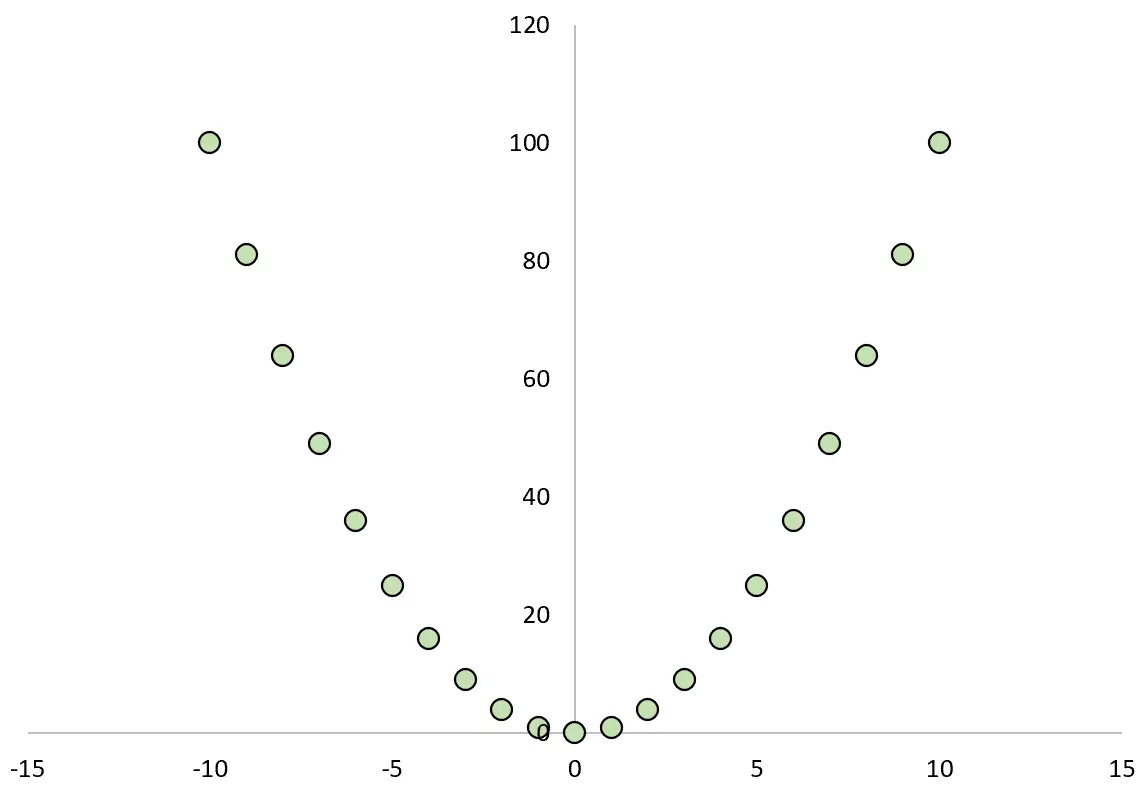
Wenn wir den Pearson-Korrelationskoeffizienten zwischen den beiden Variablen berechnen würden, würden wir feststellen, dass die Korrelation Null ist.

Obwohl X Y verursacht, ist die lineare Korrelation zwischen den beiden Variablen Null.

Beispiel 2: Quartische Relation

Angenommen, eine Variable X bewirkt, dass die Variable Y einen Wert gleich X ⁴ annimmt.

Zum Beispiel:

• Wenn X = -10, dann Y = -10 ⁴ = 10.000
• Wenn X = 0, dann ist Y = 0 ⁴ = 0
• Wenn X = 10, dann ist Y = 10 ⁴ = 10.000

Und so weiter.

Wenn wir die Beziehung zwischen X und Y darstellen, würde das so aussehen:

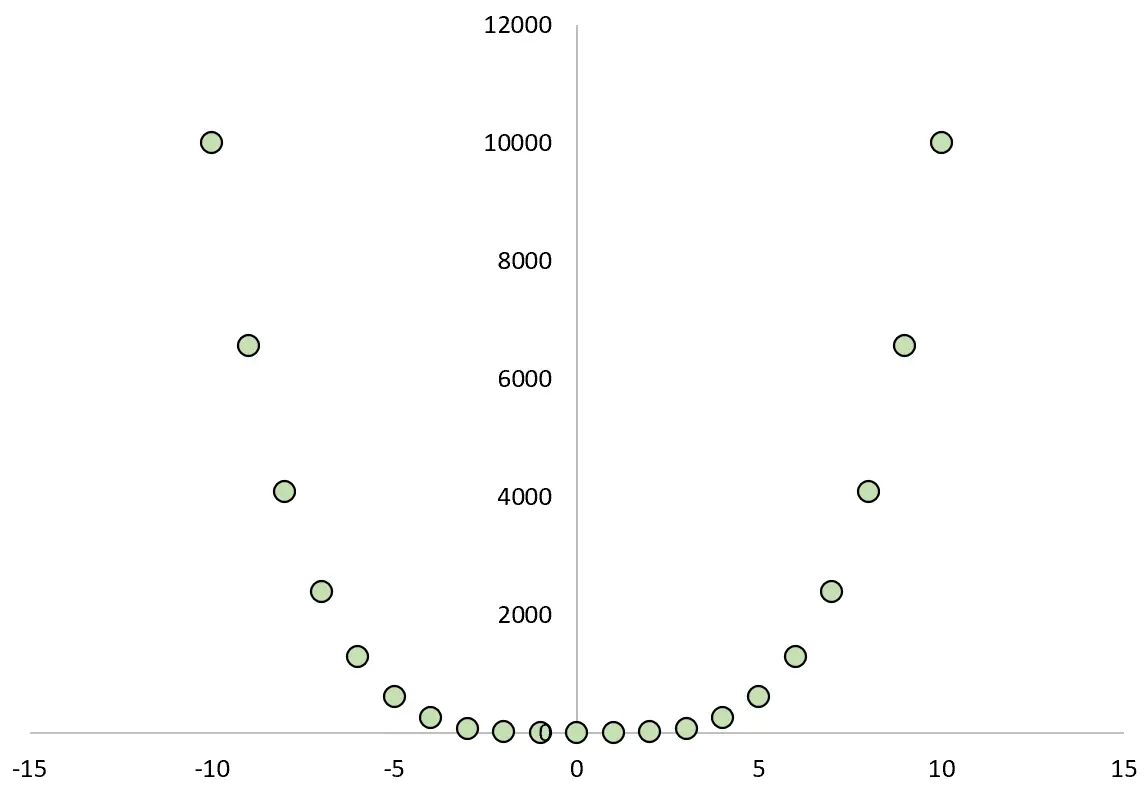
Wenn wir den Pearson-Korrelationskoeffizienten zwischen den beiden Variablen berechnen würden, würden wir feststellen, dass die Korrelation Null ist.

Wir wissen, dass X Y verursacht, aber die lineare Korrelation zwischen den beiden Variablen ist Null.

Beispiel 3: Kosinusbeziehung

Angenommen, eine Variable X bewirkt, dass die Variable Y einen Wert gleich cos(X) annimmt.

Zum Beispiel:

• Wenn X = -10, dann Y = cos(-10) = -0,83907
• Wenn X = 0, dann ist Y = cos(0) = 1
• Wenn X = 10, dann ist Y = cos(10) = -0,83907

Und so weiter.

Wenn wir die Beziehung zwischen X und Y darstellen, würde das so aussehen:

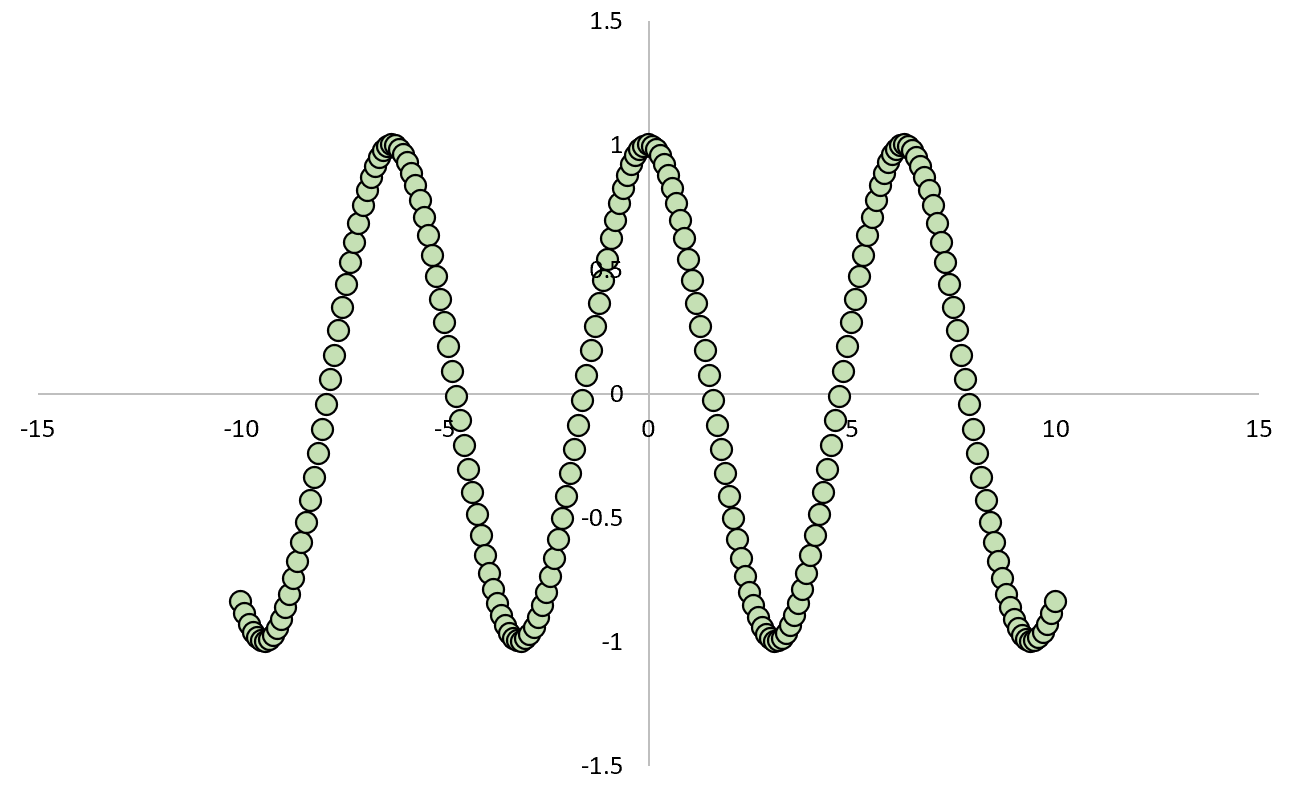
Wenn wir den Pearson-Korrelationskoeffizienten zwischen den beiden Variablen berechnen würden, würden wir feststellen, dass die Korrelation Null ist.

Wir wissen, dass X Y verursacht, aber die lineare Korrelation zwischen den beiden Variablen ist Null.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Korrelation und Kausalität:

Korrelation bedeutet keine Kausalität: 5 konkrete Beispiele
Einführung in den Pearson-Korrelationskoeffizienten
Umgekehrte Kausalität: Definition und Beispiele