Die drei annahmen der anova mit wiederholten messungen

Eine ANOVA mit wiederholten Messungen wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht, in denen in jeder Gruppe dieselben Probanden vorkommen.

Bevor wir jedoch eine ANOVA mit wiederholten Messungen durchführen, müssen wir sicherstellen, dass die folgenden Annahmen erfüllt sind:

1. Unabhängigkeit: Jede Beobachtung muss unabhängig sein.

2. Normalität: Die Verteilung der Antwortvariablen ist normalverteilt.

3. Sphärizität: Die Varianzen der Unterschiede zwischen allen Kombinationen verwandter Gruppen müssen gleich sein.

Wenn eine oder mehrere dieser Annahmen verletzt werden, können die Ergebnisse der ANOVA mit wiederholten Messungen unzuverlässig sein.

In diesem Artikel geben wir eine Erklärung für jede Annahme, wie Sie feststellen können, ob die Annahme erfüllt ist, und was zu tun ist, wenn sie nicht erfüllt ist.

Hypothese 1: Unabhängigkeit

Bei wiederholten ANOVA-Messungen wird davon ausgegangen, dass jede Beobachtung in Ihrem Datensatz unabhängig von allen anderen Beobachtungen ist.

So ermitteln Sie, ob diese Annahme erfüllt ist

Der einfachste Weg, diese Annahme zu überprüfen, besteht darin, mithilfe einer Zufallsstichprobenmethode zu überprüfen, ob jede Person im Datensatz zufällig aus der Bevölkerung ausgewählt wurde.

Bei Verwendung einer Zufallsstichprobenmethode kann davon ausgegangen werden, dass jede Beobachtung unabhängig ist.

Was tun, wenn diese Annahme nicht respektiert wird?

Wenn diese Annahme nicht erfüllt ist, handelt es sich um ein ernstes Problem, da die Werte jedes Einzelnen auf die eine oder andere Weise miteinander in Zusammenhang stehen können.

In diesem Szenario hilft oft nur die Rekrutierung von Personen für eine neue Studie mithilfe einer Zufallsstichprobenmethode.

Hypothese 2: Normalität

Bei wiederholten ANOVA-Messungen wird davon ausgegangen, dass die Verteilung der Antwortvariablen normalverteilt ist.

So ermitteln Sie, ob diese Annahme erfüllt ist

Es gibt zwei Möglichkeiten zu überprüfen, ob diese Hypothese wahr ist:

1. Erstellen Sie ein Histogramm oder einen QQ-Plot

Sie können visuell überprüfen, ob die Verteilung der Antwortvariablen annähernd normalverteilt ist, indem Sie ein Histogramm oder einen QQ-Plot erstellen.

Wenn Sie ein Histogramm erstellen, überprüfen Sie einfach, ob die Verteilung der Antwortvariablen ungefähr einer „Glockenform“ folgt. Wenn ja, können Sie oft davon ausgehen, dass die Normalitätsannahme erfüllt ist:

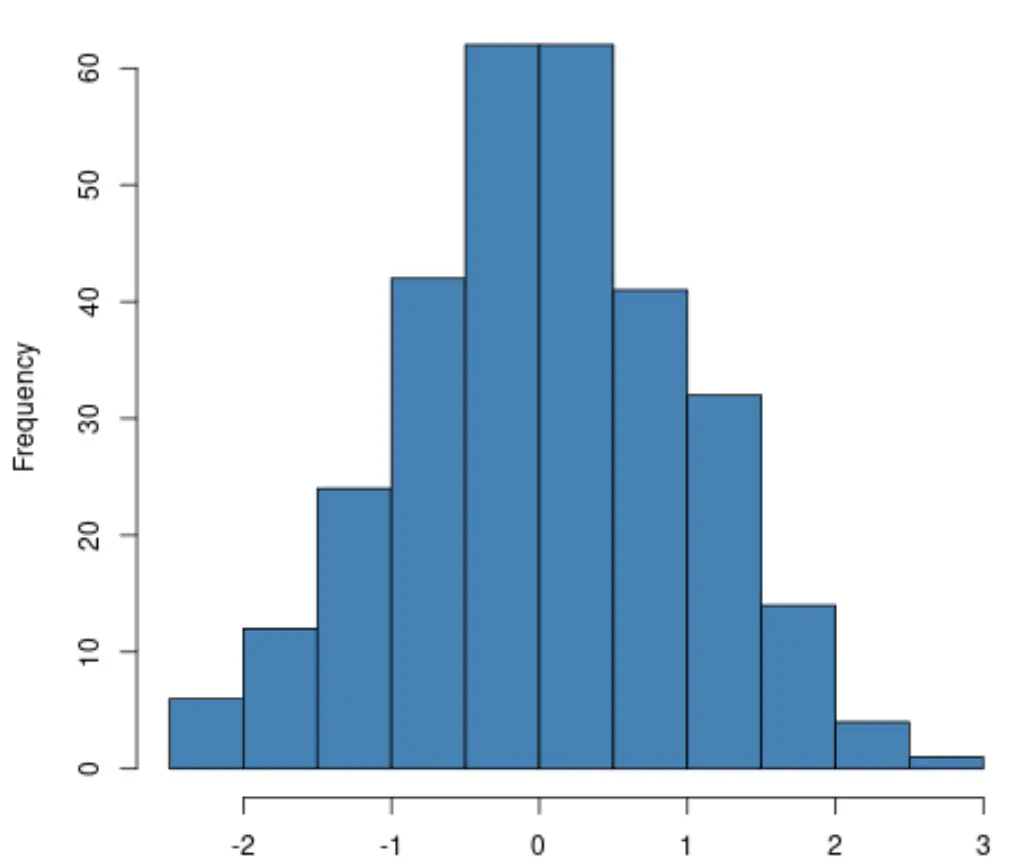
Wenn Sie ein QQ-Diagramm erstellen, prüfen Sie, ob die Datenpunkte auf einer geraden diagonalen Linie liegen. Wenn ja, können Sie im Allgemeinen davon ausgehen, dass die Normalitätsannahme erfüllt ist:

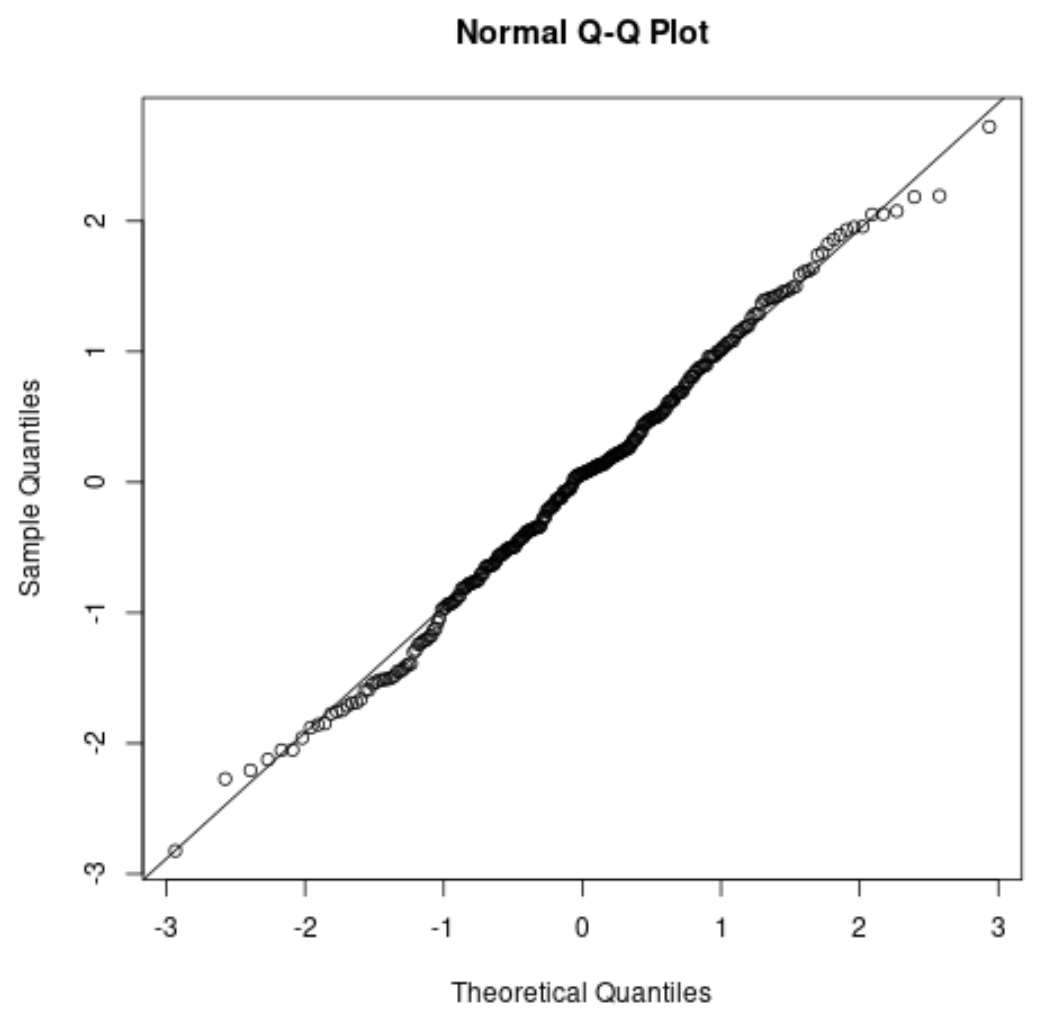
Verwandte Themen: So verwenden Sie QQ-Plots zur Überprüfung der Normalität

2. Führen Sie einen formellen statistischen Test durch

Sie können auch einen Shapiro-Wilk-Test durchführen, um die Normalität zu überprüfen. Wenn der p-Wert des Tests weniger als 0,05 beträgt, deutet dies darauf hin, dass die Daten nicht normalverteilt sind.

Beachten Sie jedoch, dass statistische Tests wie der Shapiro-Wilk-Test Ihnen bei der Arbeit mit extrem großen Stichproben fast immer sagen, dass Ihre Daten nicht normal sind.

Aus diesem Grund ist es oft am besten, Ihre Daten visuell mithilfe von Diagrammen wie Histogrammen und QQ-Diagrammen zu überprüfen. Wenn Sie sich nur die Diagramme ansehen, können Sie eine ziemlich gute Vorstellung davon bekommen, ob die Daten normalverteilt sind oder nicht.

Was tun, wenn diese Annahme nicht respektiert wird?

Im Allgemeinen gilt eine ANOVA mit wiederholten Messungen als recht robust gegenüber Verletzungen der Normalitätsannahme, solange die Stichprobengrößen groß genug sind.

Wenn die Normalitätsannahme ernsthaft verletzt wird, haben Sie zwei Möglichkeiten:

1. Transformieren Sie die Antwortwerte Ihrer Daten, sodass die Verteilungen normaler verteilt sind.

2. Führen Sie einen äquivalenten nichtparametrischen Test wie den Friedman-Test durch, der keine Normalitätsannahme erfordert.

Annahme 3: Sphärizität

Eine ANOVA mit wiederholten Messungen geht von Sphärizität aus – das heißt, die Varianzen der Unterschiede zwischen allen Kombinationen verwandter Gruppen müssen gleich sein.

Wenn diese Annahme nicht erfüllt ist, erhöht sich das F-Verhältnis und die Ergebnisse der ANOVA mit wiederholten Messungen werden unzuverlässig.

So ermitteln Sie, ob diese Annahme erfüllt ist

Um zu testen, ob diese Annahme erfüllt ist, können wir den Mauchly-Test der Sphärizität durchführen.

Dieser Test verwendet die folgende Null- und Alternativhypothese:

• H ₀ : Die Varianzen der Differenzen sind gleich
• H _A : Die Varianzen der Differenzen sind nicht gleich

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), lehnen wir die Nullhypothese ab und schließen daraus, dass die Varianzen der Differenzen nicht gleich sind.

Andernfalls können wir die Nullhypothese nicht ablehnen und daraus schließen, dass die Annahme der Sphärizität erfüllt ist, wenn der p-Wert nicht unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05).

Abhängig von der von Ihnen verwendeten Statistiksoftware sehen die Ergebnisse dieses Tests wie folgt aus:

Da der p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen und daraus schließen, dass die Annahme der Sphärizität in diesem speziellen Beispiel erfüllt ist.

Was tun, wenn diese Annahme nicht respektiert wird?

Wenn wir die Nullhypothese von Mauchlys Sphärizitätstest ablehnen, wenden wir im Allgemeinen eine Korrektur auf die Freiheitsgrade an, die zur Berechnung des F-Werts in der ANOVA-Tabelle mit wiederholten Messungen verwendet werden.

Es gibt drei Korrekturen, die wir anwenden können:

• Huynh-Feldt (am wenigsten konservativ)
• Serre-Geisser
• Untere Grenze (am konservativsten)

Jede dieser Korrekturen erhöht tendenziell die p-Werte in der ANOVA-Ausgabetabelle mit wiederholten Messungen, um der Tatsache Rechnung zu tragen, dass die Annahme der Sphärizität verletzt wird.

Mithilfe dieser p-Werte können wir dann bestimmen, ob wir die Nullhypothese der ANOVA mit wiederholten Messungen ablehnen sollten oder nicht.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur ANOVA mit wiederholten Messungen:

Eine Einführung in die ANOVA mit wiederholten Messungen
ANOVA-Rechner für wiederholte Messungen
So melden Sie die Ergebnisse einer ANOVA mit wiederholten Messungen
Einfaktorielle ANOVA und ANOVA mit wiederholten Messungen: der Unterschied