So führen sie manuell eine zweifaktorielle anova durch

Eine zweifaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht, die auf zwei Faktoren aufgeteilt wurden.

In diesem Tutorial wird erläutert, wie Sie eine zweifaktorielle ANOVA manuell durchführen.

Beispiel: Manuelle Zwei-Wege-ANOVA

Angenommen, ein Botaniker möchte wissen, ob das Pflanzenwachstum durch die Sonneneinstrahlung und die Häufigkeit des Gießens beeinflusst wird. Sie pflanzt 40 Samen und lässt sie einen Monat lang unter verschiedenen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen.

Nach einem Monat zeichnet sie die Höhe jeder Pflanze auf. Die Ergebnisse sind unten dargestellt:

In der Tabelle oben sehen wir, dass in jeder Kombination von Bedingungen fünf Pflanzen gezüchtet wurden.

Beispielsweise wurden fünf Pflanzen mit täglicher Bewässerung und ohne Sonnenlicht gezüchtet und ihre Höhen betrugen nach zwei Monaten 4,8 Zoll, 4,4 Zoll, 3,2 Zoll, 3,9 Zoll und 4,4 Zoll:

Wir können die folgenden Schritte verwenden, um eine zweifaktorielle ANOVA durchzuführen:

Schritt 1: Berechnen Sie die Quadratsumme für den ersten Faktor (Bewässerungshäufigkeit)

Zunächst berechnen wir die durchschnittliche Gesamthöhe der 40 Pflanzen:

Gesamtdurchschnitt = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Als nächstes berechnen wir die durchschnittliche Höhe aller täglich bewässerten Pflanzen:

Tagesdurchschnitt = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155

Als nächstes berechnen wir die durchschnittliche Höhe aller Pflanzen, die jede Woche bewässert werden:

Wochendurchschnitt = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15

Als nächstes berechnen wir die Summe der Quadrate für den Faktor „Bewässerungshäufigkeit“ mithilfe der folgenden Formel:

Σn(X _j – X ..) ²

Gold:

• n : die Stichprobengröße der Gruppe j
• Σ : ein griechisches Symbol mit der Bedeutung „Summe“
• X _j : der Durchschnitt der Gruppe j
• X .. : der große Durchschnitt

In unserem Beispiel berechnen wir die Quadratsumme für den Faktor „Bewässerungshäufigkeit“ wie folgt: 20(5,155-5,1525) ² + 20(5,15-5,1525) ² = 0,00025

Schritt 2: Berechnen Sie die Quadratsumme für den zweiten Faktor (Sonneneinstrahlung).

Zunächst berechnen wir die durchschnittliche Gesamthöhe der 40 Pflanzen:

Gesamtdurchschnitt = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Als nächstes berechnen wir die durchschnittliche Höhe aller Pflanzen, die nicht der Sonne ausgesetzt sind:

Durchschnitt ohne Sonne = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07

Wir werden diese Berechnung wiederholen, um die durchschnittliche Höhe von Pflanzen zu ermitteln, die verschiedenen Sonneneinstrahlungen ausgesetzt sind:

• Niedriger Sonnenscheindurchschnitt = 5,1
• Durchschnittliches durchschnittliches Sonnenlicht = 5,89
• Durchschnittlicher hoher Sonnenschein = 5,55

Als nächstes berechnen wir die Summe der Quadrate für den Faktor „Sonneneinstrahlung“ mithilfe der folgenden Formel:

Σn(X _j – X ..) ²

Gold:

• n : die Stichprobengröße der Gruppe j
• Σ : ein griechisches Symbol mit der Bedeutung „Summe“
• X _j : der Durchschnitt der Gruppe j
• X .. : der große Durchschnitt

In unserem Beispiel berechnen wir die Quadratsumme für den Faktor „Sonneneinstrahlung“ wie folgt: 10(4,07-5,1525) ² + 10(5,1-5,1525) ² + 10(5,89 -5,1525) ² + 10(5,55-5,1525) ² = 18,76475

Schritt 3: Berechnen Sie die Summe der darin enthaltenen Quadrate (Fehler)

Als nächstes berechnen wir die Summe der Quadrate, indem wir die Summe der Quadrate der Differenzen zwischen jeder Kombination von Faktoren und den einzelnen Pflanzenhöhen bilden.

Beispielsweise beträgt die durchschnittliche Höhe aller täglich bewässerten Pflanzen ohne Sonneneinstrahlung 4,14. Wir können dann die Summe der Quadrate der Differenzen für jede dieser einzelnen Pflanzen wie folgt berechnen:

• SS für tägliches Gießen und ohne Sonne: (4,8-4,14) ² + (4,4-4,14) ² + (3,2-4,14) ² + (3,9-4,14) ² + (4,4-4,14) ² = 1,512

Wir können diesen Vorgang für jede Kombination von Faktoren wiederholen:

• SS für tägliche Bewässerung und wenig Sonnenlicht: 0,928
• SS für tägliche Bewässerung und durchschnittlicher Sonnenschein: 1.788
• SS für tägliche Bewässerung und starke Sonneneinstrahlung: 1,648
• SS für wöchentliches Gießen ohne Sonne: 0,34
• SS für wöchentliches Gießen und wenig Sonnenlicht: 0,548
• SS für wöchentliche Bewässerung und durchschnittlicher Sonnenschein: 0,652
• SS für wöchentliches Gießen und starkes Sonnenlicht: 1.268

Wir können dann die Summe aller dieser Werte bilden, um die Summe der darin enthaltenen Quadrate (Fehler) zu ermitteln:

Summen der Quadrate innerhalb = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684

Schritt 4: Berechnen Sie die Gesamtsumme der Quadrate

Dann können wir die Gesamtsumme der Quadrate berechnen, indem wir die Summe der Differenzen zwischen der Höhe jeder Pflanze und dem Gesamtdurchschnitt bilden:

Gesamtsumme der Quadrate = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Schritt 5: Berechnen Sie die Summe der Quadratwechselwirkungen

Als nächstes berechnen wir die Summe der Quadratwechselwirkungen mithilfe der folgenden Formel:

• Interaktion SS = SS Gesamt – SS-Faktor 1 – SS-Faktor 2 – SS-Innenraum
• SS-Interaktion = 28,45975 – 0,00025 – 18,76475 – 8,684
• SS-Interaktion = 1,01075

Schritt 6: Vervollständigen Sie die ANOVA-Tabelle

Abschließend tragen wir die Werte aus der zweifaktoriellen ANOVA-Tabelle ein:

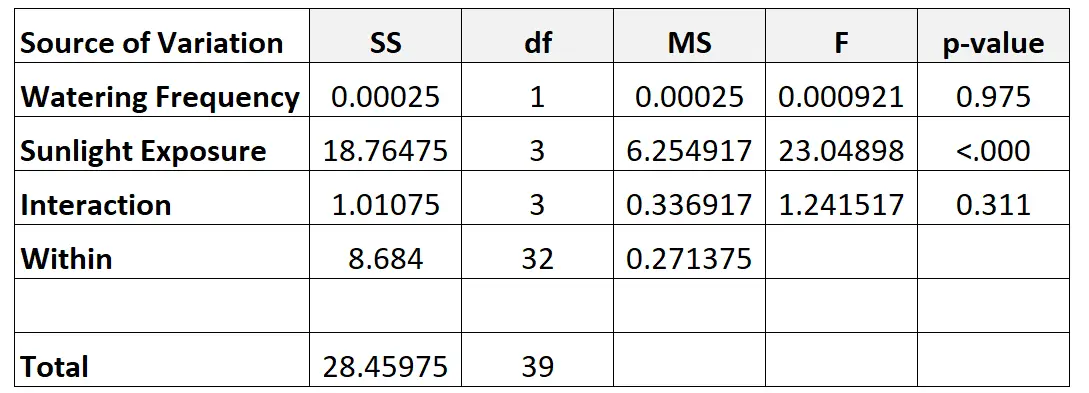
So haben wir die verschiedenen Zahlen in der Tabelle berechnet:

• df Bewässerungshäufigkeit: d-1 = 2-1 = 1
• df Sonneneinstrahlung: k-1 = 4-1 = 3
• dfInteraktion : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• Gesamt-df: n-1 = 40-1 = 39
• MS: SS/DF
• Bewässerungshäufigkeit F : MS/MS-Bewässerungshäufigkeit im Innenbereich
• F Sonneneinstrahlung : MS/MS-Sonneneinstrahlung in Innenräumen
• Interaktion F : Interaktion MS / MS Innerhalb
• p-Wert-Bewässerungshäufigkeit : Der p-Wert, der dem F-Wert von 0,000921 mit dem Zähler df = 1 und dem Nenner df = 32 entspricht
• P-Wert der Sonneneinstrahlung : der p-Wert, der dem F-Wert von 23,04898 mit dem Zähler df = 3 und dem Nenner df = 32 entspricht
• p-Wert-Interaktion : Der p-Wert, der dem F-Wert von 1,241517 mit dem Zähler df = 3 und dem Nenner df = 32 entspricht

Anmerkung Nr. 1: n = Gesamtzahl der Beobachtungen, j = Anzahl der Stufen für die Bewässerungshäufigkeit, k = Anzahl der Stufen für die Sonneneinstrahlung.

Hinweis Nr. 2 : Die p-Werte, die dem F-Wert entsprechen, wurden mit dem F-Verteilungsrechner berechnet.

Schritt 7: Interpretieren Sie die Ergebnisse

Aus der ANOVA-Tabelle können wir Folgendes beobachten:

• Der p-Wert für die Wechselwirkung zwischen Bewässerungshäufigkeit und Sonneneinstrahlung betrug 0,311 . Dies ist bei α = 0,05 statistisch nicht signifikant.
• Der p-Wert für die Bewässerungshäufigkeit betrug 0,975 . Dies ist bei α = 0,05 statistisch nicht signifikant.
• Der p-Wert für Sonnenexposition betrug <0,000 . Dies ist statistisch signifikant bei α = 0,05.

Diese Ergebnisse deuten darauf hin, dass die Sonneneinstrahlung der einzige Faktor ist, der einen statistisch signifikanten Einfluss auf die Pflanzenhöhe hat.

Und da es keinen Wechselwirkungseffekt gibt, ist der Effekt der Sonneneinstrahlung bei jeder Bewässerungshäufigkeit gleichbleibend.

Einfach ausgedrückt: Ob eine Pflanze täglich oder wöchentlich gegossen wird, hat keinen Einfluss darauf, wie sich Sonneneinstrahlung auf eine Pflanze auswirkt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu ANOVAs:

So führen Sie manuell eine einfaktorielle ANOVA durch
So führen Sie manuell eine ANOVA mit wiederholten Messungen durch
Der vollständige Leitfaden: So melden Sie Ergebnisse der zweifaktoriellen ANOVA